Строят множество решений каждого неравенства.
1.1. По точкам пересечения с осями координат строят границу полуплоскости каждого неравенства. Это прямая, значения коэффициента и свободного члена которой соответственно равны значениям коэффициента и свободного члена неравенства. Для данного примера это прямые Для расчета точки пересечения прямой с осью 0X1 значение переменной х2 принимается равным нулю. Для расчета точки пересечения прямой с осью ОХ2 значение переменной xl принимается равным нулю. Пример расчета координат точек пересечения границ полуплоскостей ОДР с осями координат приведен в табл. 2.
Таблица 2.
1.2. Определяют искомые полуплоскости, содержащие множество решений каждого неравенства. Прямая делит плоскость на две полуплоскости. Только одна из них содержит множество решений неравенства. Для ее определения необходимо задать произвольную точку, предположительно принадлежащую множеству решений неравенства. Удобно взять точку (10, 10), координаты которой необходимо подставить в каждое неравенство системы неравенств. Если неравенство выполняется в этой точке (знак неравенства остается прежним), то оно выполняется и во всех точках полуплоскости, содержащей точку (10, 10):
10 < 18 - неравенство выполняется в точке (10,10). Содержащую множество решений неравенства полуплоскость заштриховывают.
|
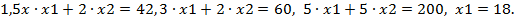
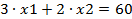
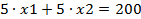
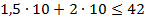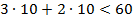- неравенство выполняется в точке (10,10):
- неравенство выполняется в точке (10,10);
- неравенство выполняется в точке (10,10);
