Третья задача анализа на чувствительность
Цель работы: провести анализ влияния изменения цен на производственную ситуацию. Теоретическое обоснование В третьей задаче анализа на чувствительность находятся такие пределы изменения иен на производимую продукцию, что оптимальный план останется неизменным. Находятся также такие пределы изменения цен при неизменном оптимальном плане, в которых значение целевой функции не уменьшается. Цены на продукцию Если целевая функция при изменении угла наклона совпадет с одной из границ ОДР или отсечет какую - либо часть ОДР, то изменится оптимальный план производства юбок и брюк. Необходимо подобрать такие пределы изменения цен на юбки и брюки, при которых целевая функции не будет отсекать ОДР, т. е. при вращении ЦФ против часовой стрелки границей перемещения будет прямая «запас ткани»; при вращении по часовой стрелке такой границей будет прямая «трудоемкость». Чтобы рассчитать предельные значения цен на юбки и брюки при неизменном оптимальном плане, приравняем тангенсы углов наклона связующих прямых ОДР и целевой функции. Получатся следующие соотношения: При вращении ЦФ против часовой стрелки до прямой «ткань» значение тангенса уменьшается, что соответствует меньшему значению угла наклона ЦФ; значение тангенса может уменьшаться либо за счет увеличения пусть пусть При вращении ЦФ по часовой стрелке до прямой «трудоемкость» значение тангенса ЦФ увеличивается. Значение тангенса может увеличиваться либо за счет уменьшения пусть пусть При изменении цен на юбки и брюки в пределах 37,5< Ход выполнения В строке «Целевая функция» (ЦФ) таблицы исходных данных (табл.7) измените цену юбки до 40 руб. за 1 штуку. Прямая целевой функции на рис.1 повернется в таком случае против часовой стрелки и отсечет часть ОДР. Посмотрите, как изменится оптимальный план и доход. Теперь измените цену на юбки до 100 руб. Целевая функция повернется по часовой стрелке и снова отсечет часть ОДР. Теперь то же самое проделайте с ценой на брюки. Решение третьей задачи анализа на чувствительность в EXCEL не представляется сложным. Обязательным условием решения третьей задачи анализа на чувствительность в EXCEL является наличие оптимального решения в соответствующих ячейках. Трудности могут возникнуть с автоматическим определением связующих прямых. Для автоматического определения программой связующих прямых и расчета пределов изменения цен на юбки и брюки необходимо: 1. Составить таблицу (табл. 9) для записи решений третьей задачи. Такая таблица может располагаться в любом месте поля EXCEL. Таблица 9
С помощью табл. 9 обеспечивается автоматизация расчета критических значений 2.В табл. 9 заносят формулы расчета критических значений В первом столбце определяется тип прямой. Для третьей задачи интересными являются только связующие прямые, поскольку они образуют точку оптимального плана, через которую проходит целевая функция. В первую строку столбца «Тип прямой» табл. 9 запишите формулу, В первую строку столбца «Коэффициенты при xl» запишите формулу, В первую строку столбца «Коэффициенты при x2» запишите формулу, В первую строку столбца «Критические значения В первую строку столбца «Критические значения 3. Из столбцов «Критические значения Задание: 1. Подставьте полученные значения поочередно в соответствующие ячейки EXCEL, объясните, почему для обозначения интервалов изменения цен используются знаки строгого неравенства? 2. Самостоятельно укажите интервалы изменения цен на продукцию, в границах которых значение дохода не уменьшится.
|

 =60,
=60, 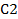 =50 - это компоненты тангенса угла наклона целевой функции. Для того чтобы в этом убедиться, приведем целевую функцию к виду записи уравнения прямой
=50 - это компоненты тангенса угла наклона целевой функции. Для того чтобы в этом убедиться, приведем целевую функцию к виду записи уравнения прямой 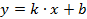 . Получим
. Получим  ,где (-60/50) - тангенс угла наклона целевой функции. Следовательно, изменение цен С1 и
,где (-60/50) - тангенс угла наклона целевой функции. Следовательно, изменение цен С1 и 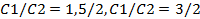 .
. руб.;
руб.;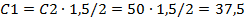 руб.
руб.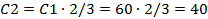 руб.
руб.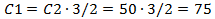 руб.
руб.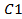 <75 и 40<
<75 и 40< 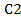 <80 соответственно оптимальный план выпуска юбок и брюк X = (12, 12) останется неизменным.
<80 соответственно оптимальный план выпуска юбок и брюк X = (12, 12) останется неизменным.


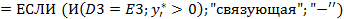 . При записи формулы используйте вместо обозначения оценки (
. При записи формулы используйте вместо обозначения оценки ( 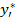 ) ссылку на соответствующую ячейку. Размножьте эту формулу по другим строкам столбца.
) ссылку на соответствующую ячейку. Размножьте эту формулу по другим строкам столбца. .Размножьте формулу по остальным строкам столбца.
.Размножьте формулу по остальным строкам столбца.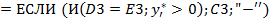 Размножьте формулу по остальным строкам столбца.
Размножьте формулу по остальным строкам столбца. - ссылка на ячейку с коэффициентом при xl;СЗ - ссылка на ячейку с коэффициентом при х2; $С$9- ссылка на ячейку с ценой на брюки (см. табл. 7). Размножьте ее по остальным строкам.
- ссылка на ячейку с коэффициентом при xl;СЗ - ссылка на ячейку с коэффициентом при х2; $С$9- ссылка на ячейку с ценой на брюки (см. табл. 7). Размножьте ее по остальным строкам.


