Построение градиента и целевой функции.Нахождение точки оптимального плана. Применение алгоритма «Поиск решения» Цель работы: построить целевую функцию ЗЛП и с помощью алгоритма «Поиск решения» найти точку оптимального плана. Теоретическое обоснование Приравняем целевую функцию а)построить градиент и провести к нему перпендикуляр; б)приравнять целевую функцию к какому - либо числу Градиент - вектор, который показывает направление наискорейшего возрастания целевой функции. Градиент строится из начала координат. Координаты градиента - это частные производныецелевойфункции Чтобы найти точку оптимального плана, среди точек многоугольника области допустимых решений ABCDE (рис. 1) необходимо найти такую, в которой функция Ход выполнения 1. Для построения градиента внесите в ячейки поля EXCEL коэффициенты Добавьте строку для расчета координат градиента. С помощью ссылок на коэффициенты целевой функции запишите расчет координат градиента в ячейки Е10 и G10 (табл.6). Градиент строится в диаграмме «Точечная» аналогично процедуре построения прямых ОДР (п. 3, абзац 2 лабораторной работы 1).
Таблица 6
2. Построение целевой функции проводится по точкам пересечения с осямикоординат. В поле расчета координат точек пересечения прямых ОДР с осями ОХ1 и ОХ2скопируйте формулы из строки 3 в строку 9 (табл. 6). В ячейку D9 запишите любое положительное числовое значение В «Исходные данные» диаграммы EXCEL добавьте ограничение «Целевая функция» согласно второму шагу построения (п. 3, второй абзац лабораторной работы 1). Построенная целевая функция может располагаться как на пересечении с ОДР, так и за пределами ОДР в зависимости от значения 3. Чтобы обеспечить передвижение целевой функции по графику EXCEL до точки оптимума, необходимы дополнительные построения. Добавьте после строки «Целевая функция» в табл. 6 строку «Допустимый план», в ячейках В11 и С11 которой будут содержаться допустимые значения Вставьте справа от расширенной матрицы ЗЛП еще один столбец, в соответствующих строках которого будут записываться формулы левых частей ограничений и целевой функции (см. табл. 7) Запишите в ячейку ЕЗ табл. 7 формулу =ВЗ*В11 + СЗ*С11. Скопируйте эту формулу в остальные ячейки столбца Е табл. 7. Вместо любого значения а>0 в ячейке D9 установите ссылку на ячейку Е9(см. табл. 7). Для передвижения целевой функции по диаграмме достаточно «привязать» целевую функцию к координатам точки допустимого плана (точки оптимума). Постройте на диаграмме точку допустимого плана. В меню «Исходные данные» графического редактора выберите опцию «добавить ряд». В окно «Значения X» с помощьюссылки вставьте адрес ячейки со значением Теперь введите в ячейки допустимого плана любые допустимые значения Щелкните по точке допустимого плана два раза. Затем мышкой перетащите точку в любое место графика. Целевая функция при этом будет перемещаться параллельнымпереносом. Добейтесь, чтобы прямая целевой функцииbпереместилась до крайней точки соприкосновения с ОДР. Совместите точку допустимого плана с крайней точкой соприкосновения ОДР и целевой функции. В ячейках допустимого плана появятся значения, близкие оптимальным. Таблица 7
4. Для нахождения оптимального плана воспользуйтесь встроенной в EXCELпроцедурой «Поиск решения». Основныеэтапы выполнения процедуры «Поиск решения»: 1. В опции «Сервис» выберите «Поиск решения». 2. В диалоговом окне «Целевая ячейка» сделайте ссылку на ячейку, содержащую значение целевой функции. 3. В окне «Ограничения» нажмите кнопку «Добавить». Появится новоедиалоговое окно, в котором необходимо записать левую и правую части ограничений в виде ссылок на соответствующие ячейки:
Рис.2 Необходимо добавить таким способом все ограничения, в том числе и условия неотрицательности переменных 4. В окне «Изменяя ячейки» сделайте ссылки на ячейки, содержащие значение допустимого плана 5. После записи всех ограничений в диалоговое окно «Ограничения» нажмите кнопку «Выполнить». 6.После окончания алгоритма загорится диалоговое окно. Выберите«Сохранить найденное решение». Необходимо с помощью мышки и клавиши Shift выделить все три типа отчета и нажать ОК. Контрольные вопросы 1. Что является графическим отображением области допустимых решений ЗЛИ? 2. На каких участках области допустимых решений может находиться оптимальное решение ЗЛП? 3. Что является множеством решений неравенства? 4. Какие существенные недостатки не позволяют широко применять графический метод для решения задач линейного программирования? 5. Что такое расширенная матрица? Задание: докажите с помощью построенной диаграммы основное свойство линии уровня.
|
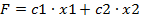к постоянной величине а: 
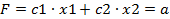. Меняя значение а, получим семейство параллельных прямых, каждая из которых называется линией уровня. Линия уровня - геометрическое место точек, в которых целевая функция принимает одно и то же значение, равное а. Целевая функция не зафиксирована в определенном положении относительно начала координат (а может принимать различные значения). Ее можно перемешать параллельным переносом, как в направлении возрастания, так и по направлению убывания. Целевая функция перпендикулярна градиенту. На графике ее можно отобразить двумя способами:
затем рассчитать координаты точек пересечения с осями ОХ и ОУ.
Действительно, 
Получаем градиент С(60;50).
, 
при переменных XI и 
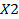целевой функции и соответствующие подписи так, как это показано в табл. 6.
)
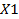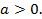
плана ЗЛП. Выделите эти ячейки с помощью заливки.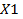
допустимого плана 
В окно «Значение У» с помощью ссылки вставьте адрес ячейки со значением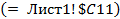 
. Для точки допустимого плана установите крупный значок маркера.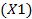
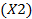
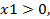
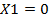
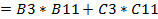
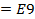
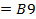
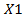и 
