Первая и вторая задачи анализа на чувствительностьЦель работы: проанализировать возможные изменения запасов различных ресурсов в конкретной производственной ситуации; определить ценность каждого ресурса и наиболее ценные ресурсы. Теоретическое обоснование А. Пусть вектор X = (12, 12) - оптимальный план ЗЛП (1 - 3), что соответствует производству двенадцати юбок и двенадцати брюк соответственно. Подставим значение оптимального плана в неравенства системы линейных неравенств, где, в таком случае, левая часть ограничения обозначает количество используемой ткани при оптимальном плане производства юбок и брюк, а правая часть показывает суточный запас ткани:
12 < 18 - то же самое можно сказать о резерве спроса на юбки. С точки зрения экономии, запасы некоторых ресурсов были излишними, потому что они не были использованы в процессе производства. Суточную потребность в накладных расходах, например, можно уменьшить. А на какую величину? Наверно, на такую, которая не повлияла бы на размер получаемого дохода и объем выпуска продукции. Отсюда вытекает один из вопросов первой задачи анализа на чувствительность: «Запасы, каких ресурсов и на какую в еличину можно уменьшить так, чтобы оптимальный план и доход осталис ь неизменными?» В ситуации, когда, например, спрос на юбки падает до нуля, производство юбок разумно было бы прекратить и увеличить выпуск брюк. Для того чтобы доходы при этом не упали, целесообразно пересмотреть план выпуска брюк. Это значит, что необходимо изменить и объем запасов производственных ресурсов, необходимых для производства брюк. Однако существуют разумные пределы запасов. Они обусловлены экономическими причинами - отсутствие складских помещений, ограниченные возможности доставки и др. Задача минимум в такой ситуации - рассчитать заранее, запасы каких ресурсов и в каких пределах выгодно увеличить. Отсюда второй вопрос первой задачи анализа на чувствительность: «Запасы каких ресурсов и на какую величину молено увеличить, чтобы увеличился доход от реализации продукции?» Как видно из графического решения (рис. 1) и анализа количества использованных при оптимальном плане ресурсов, ограничения на ткань и трудоемкость соответствуют связующим прямым. Основное свойство связующихпрямых — они проходят через точку оптимума и одновременно являются сторонами многоугольника ОДР. Ресурсы, соответствующие связующим прямым, сдерживают рост оптимального плана, что легко заметить, если подставить оптимальный план выпуска юбок и брюк в ограничения ЗЛП. Левые и правые части ограничений на ткань и трудоемкость в оптимальном плане равны. Эти ресурсы, таким образом, используются полностью. Чтобы выяснить, запас, каких ресурсов необходимо увеличивать, а каких уменьшать, проведем следующие действия. Уменьшим, например, запасы ткани и трудоемкости. В результате при плане X = (12, 12) знаки ограничений перестанут выполняться, и система ограничений ЗЛП станет несовместной. Очевидно, что уменьшение запасов ткани и трудоемкости вызовет уменьшение производства юбок и брюк, что приведет к уменьшению дохода. Поэтому проводить уменьшение запаса дефицитных ресурсов (тех, которые соответствуют связующим прямым и используются полностью в оптимальном плане, их ценность строго больше нуля) нет смысла. Их увеличение, напротив, может привести к увеличению значения оптимального плана, а значит, и к увеличению значения дохода. Дефицитные ресурсы, увеличение запаса которых не приводит к увеличению значения дохода, назовем блокирующими. Уменьшение запасов накладных расходов и величины спроса на юбки, напротив, целесообразно. Как видно из примера, эти ресурсы используются не полностью в оптимальном плане. Они являются недефицитными (не используются полностью в оптимальном плане.Соответствующие недефицитным ресурсам прямые могут проходить через точку оптимума, но не образуют одновременно сторону многоугольника ОД; могут образовывать сторону ОДР, но не содержат одновременно точку оптимума.). Поскольку прямая, соответствующая ресурсу «трудоемкость», не имеет ни одной общей точки с ОДР, такой недефицитный ресурс называют избыточным. Теперь можно сформулировать ответ на первую часть первого и второго вопросов первой задачи анализа на чувствительность о том, запасы каких ресурсов целесообразно увеличивать или уменьшать. Запасы дефицитных ресурсов целесообразно увеличивать, запасы недефицитных ресурсов необходимо уменьшать. Запасы блокирующих ресурсов нецелесообразно изменять. Для ответа на вторую часть первого и второго вопросов первой задачи анализа на чувствительность о том, на какую величину целесообразно изменять запасы ресурсов, необходимо провести специальные расчеты. Увеличение или уменьшение запаса ресурса соответствует изменению значения свободного члена в уравнении прямой Расчет изменения запаса ресурсов проводится по следующему алгоритму: 1. Удаляют анализируемый ресурс с графика ОДР ЗЛП. 2.Находят новую ОДР без учета стертого ресурса. 3. Определяют новую точку оптимума на новой ОДР с помощью графического метода. 4. Определяют значение запаса ресурса в новой точке оптимума. Для этогоподставляют координаты новой точки оптимума в уравнение прямой анализируемого ресурса. 5.Для определения целесообразного изменения запаса ресурса находятразницу между значением запаса ресурса в новой точке оптимума и исходнымзначением запаса ресурсов. Б. Для определения ценности каждого ресурса решают вторую задачу анализа на чувствительность. Цель второй задачи анализа на чувствительность -установить, запасы каких ресурсов и в каких пределах необходимо увеличивать в первую очередь при прочих равных условиях? Для решения второй задачи анализа на чувствительность используется понятие «ценность единицы ресурса»: Экономический смысл ценности i - го ресурса: оценка Ход выполнения А. В поле EXCEL строим таблицу (табл. 8): Таблица 8
Примечание. F° - значение целевой функции при оптимальном плане X ° = (12, 12); Используемые в таблице формулы расчета значений:
Заполняем первые три столбца табл.8. После этого реализуетсяследующий алгоритм. Алгоритм расчета целесообразного прироста запаса ресурсов 1. Предположим, что запасы соответствующего изменяемого ресурсабесконечны. «Стираем» ресурс с диаграммы EXCEL. Для «стирания» достаточно удалить значение запаса ресурса 2. Проводим соответствующие изменения в процедуре «Поиск решения».Дляэтого в окне «Ограничения» необходимо удалить формулу для ресурса 3. Используя «Поиск решения», находим новый оптимальный план. 4. Заносим новые значения дохода 5. Восстанавливаем «стертую» прямую, заносим первоначальное значение ресурса в соответствующую ячейку EXCEL. Добавляем «стертое» ограничение в окно «Ограничения» процедуры «Поиск решения». 6. Теперь можно приступить к изменению запаса другого ресурса (см. п. Iданного алгоритма). По результатам проведенного алгоритма видно, что целесообразно увеличить запасы ткани и трудоемкости до 60 и 69 единиц соответственно. При увеличении запаса ткани на 18 метров доход возрастет на 180 рублей и составит 1500 рублей. А при увеличении запаса трудоемкости на 9 человеко-часов значение дохода возрастет на 135 рублей и составит 1455 рублей.
Б. Решение второй задачи на чувствительность запишите с помощью ссылок в виде формулы EXCEL в последний столбец табл. 8. При этом используйте данные, рассчитанные в табл.8 при решении первой задачи анализа на чувствительность. Из последнего столбца табл.8 видно, что дефицитные ресурсы имеют оценки Наиболее ценным является второй ресурс (трудоемкость). Используя полученные во второй задаче анализа на чувствительность результаты, убедимся, что Задание: проверьте результаты второй задачи анализа на чувствительность с помощью полученных в процедуре «Поиск решения» отчетов.
|
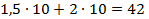-выполняется знак равенства между левой и правой частями. Разница между правой и левой частями ограничения равна нулю, значит, ресурс используется полностью при оптимальном плане;
-запас трудоемкости использован полностью при оптимальном плане выпуска юбок и брюк;
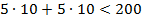-судя по этому ограничению, сумма накладных расходов использована не полностью, т. к. 120<200;
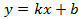. Поэтому на графике изменение запаса ресурса выглядит как перемещение соответствующей прямой параллельным переносом по координатной плоскости.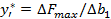
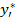показывает, на сколько единиц изменится значение дохода при изменении запаса i - го ресурса на единицу.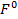
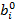
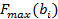
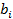
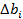
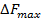
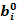- исходное значение запаса i - го ресурса; 
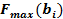- значение целевой функции в новой точке оптимума при переносе i - го ресурса; 
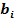- значение запаса i - го ресурса после переноса i - й прямой; 
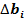- значение приращения запаса i - го ресурса; 
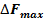- приращение целевой функции при увеличении запаса i - го ресурса на 
;
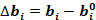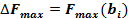- F°.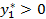
, недефицитные и избыточные ресурсы имеют оценки 
.
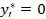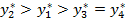. Действительно, 
.
