Графический метод решения задач линейного программирования

Графический метод применяется для решения задач линейного програм­мирования с двумя переменными (n = 2) и m ограничениями. Для решения практических задач большой размерности он является неприемлемым. Однако он обладает рядом достоинств, связанных с возможностью наглядно предста­вить свойства целевой функции ЗЛП и области допустимых решений (ОДР), а также проиллюстрировать взаимное соответствие между угловыми точками ОДР ЗЛП и допустимыми базисными решениями, что используется при изу­чении ряда других тем из данных курсов.

Для отработки алгоритма решения задач графическим методом целесооб­разно воспользоваться известными возможностями пакета EXCEL. Это позво­лит сократить время решения каждой задачи и получить наиболее полное представление о границах применения и особенностях графического метода.

Основные этапы решения ЗЛП графическим методом:

1. Построение области допустимых решений.

2. Построение градиента.

3. Построение целевой функции (ЦФ).

4. Нахождение точки оптимума (ТО).

5. Проверка значения точки оптимума и определение максимального значения целевой функции.

Графический метод решения, анализ на чувствительность и симплексная процедура рассматриваются на примере следующей производственной ситуа­ции:

Швейный цех выпускает юбки и брюки. Суточные расходы материалов и цена готовых изделий представлены в табл. 1.

Таблица I

Наименование ресурса	Расход на одну юбку	Расход на одни брюки	Запасы ресурсов
Ткань, м	1,5
Трудоемкость, чел. - час
Накладные расходы, руб.
Цена, руб.

 

Требуется определить оптимальный план производства юбок и брюк, та­кой, чтобы доход от реализации изделий был максимальным, если известно, что суточный спрос на юбки не превышает 18 штук.

Данная производственная ситуация может быть представлена в виде за­дачи линейного программирования:

(1)

(2)

(3)

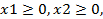которая состоит из целевой функции (1), системы ограничений (2) и условий неотрицательности переменных xl и х2 (3).