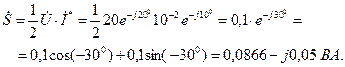МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
2.1. Гармоническое колебание
Гармоническое колебание должно записываться [1] в канонической форме
где Если гармонический сигнал представлен не в канонической форме (2.1), то его необходимо преобразовать с использованием тригонометрических соотношений, приведенных в табл. 2.1. Таблица 2.1
Если сигнал задан в виде
Примеры преобразований гармонического сигнала в каноническую форму показаны в табл. 2.2.
2.2. Комплексная амплитуда
Для гармонического сигнала (тока или напряжения)
комплексная амплитуда равна
Пусть ток равен В табл. 2.2 приведены примеры записи мгновенных значений гармонических сигналов, соответствующих им канонических форм и комплексных амплитуд.
Таблица 2.2
Проведите необходимые преобразования самостоятельно.
2.3. Комплексные числа
Комплексные числа могут записываться в алгебраической и показательной формах
где
В табл. 2.3 приведены комплексные числа в алгебраической форме и результаты их преобразования в показательную форму (проведите самостоятельно необходимые вычисления, связанные с переходом от алгебраической формы к показательной и наоборот). Полезно запомнить следующие соотношения
Рассмотрим операции с комплексными числами. Пусть заданы два комплексных числа в виде
то есть сложение и вычитание комплексных чисел удобно проводить в алгебраической форме. Если хотя бы одно из этих чисел задано в показательной форме, то его необходимо представить в алгебраическом виде, например,
При необходимости результат можно представить в показательной форме
Таблица 2.3
Найдем разность этих же чисел
Проведите вычисления самостоятельно. На рис. 2.1 показана программа вычислений в среде MathCAD.
Рис. 2.1
Умножение и деление комплексных чисел удобно проводить в показательной форме:
Примеры расчета показаны в табл. 2.4. Таблица 2.4
Проведите вычисления самостоятельно. Если одно из чисел представлено в алгебраической форме, то его необходимо перевести в показательную форму, примеры показаны в табл. 2.3. Полезно использовать соотношение (устранение комплексности в знаменателе дроби)
Комплексно-сопряженными называют числа
Проведем вычисления по устранению комплексности знаменателя, приведенные в табл. 2.5. Таблица 2.5.
Вычисления из табл. 2.5 можно выполнить, преобразовав числа из алгебраической формы в показательную, как показано в табл. 2.6. Таблица 2.6.
Проведите вычисления в табл. 2.5 и табл. 2.6 самостоятельно. На рис. 2.2 показана программа вычислений в среде MathCAD.
Рис. 2.2
2.4. Векторная диаграмма
Векторная диаграмма электрической цепи – это совокупность векторов, соответствующих гармоническим токам и напряжениям цепи, длина каждого вектора равна амплитуде (или действующему значению) сигнала, а угол наклона вектора к горизонтальной оси – начальной фазе сигнала. Для построения векторной диаграммы простой цепи необходимо использовать известные связи начальных фаз тока и напряжения в элементах цепи: - в сопротивлении напряжение совпадает по фазе с током, сдвиг фаз между ними равен нулю; - в индуктивности напряжение опережает по фазе ток на 900 (на - в емкости напряжение отстает по фазе от тока на 900 (на При построении диаграммы необходимо использовать уравнения первого и второго законов Кирхгофа в векторной форме. Рассмотрим цепь, показанную на рис. 2.3. Мгновенные значения гармонических токов и напряжений обозначены строчными (маленькими) латинскими буквами.
Рис. 2.3
Цепь представляет собой параллельное соединение двух ветвей, одна из которых является последовательным соединением элементов
Рис. 2.4
Напряжение на напряжению Рассмотрим цепь в виде последовательного соединения сопротивления, индуктивности, емкости и источника напряжения, показанную на рис. 2.5 (она будет использоваться в лабораторной работе).
Рис. 2.5
Рис. 2.6 вующие векторы изображены на рис. 2.5 с произвольной длиной. Сумма этих напряжений равна ЭДС источника Построим векторную диаграмму цепи, показанной на рис. 2.7а. В цепи последовательно соединены индуктивность
Рис. 2.7
Ток через сопротивление совпадает по фазе с напряжением
2.5. Комплексные сопротивление и проводимость участка цепи
Комплексные сопротивления и проводимости элементов цепи приведены в табл. 2.7. Для сопротивления В общем случае комплексное сопротивление можно записать в виде
где
где Таблица 2.7.
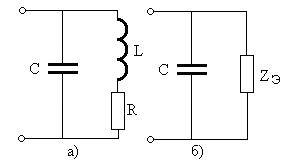
Реактивное сопротивление емкости Если реактивное сопротивление положительно (реактивная проводимость отрицательна), то цепь имеет индуктивный характер, а иначе – емкостный. При последовательном соединении элементов их комплексные сопротивления складываются, а при параллельном суммируются их комплексные проводимости. Сопротивление смешанной цепи рассчитывается следующим образом. В цепи выделяются простые фрагменты с последовательным или параллельным соединением, вычисля- ются их полные комплексные сопротивления (проводимости) и эти фрагменты заменяются одним эквивалентным элементом. Цепь упрощается, и процедура вновь повторяется. Рассмотрим пример вычисления комплексного сопротивления цепи, показанной на рис. 2.8а при
Рис. 2.8
В цепи имеется фрагмент с простым параллельным соединением элементов
Заменяя выбранный фрагмент эквивалентным элементом с комплексным сопротивлением
Подставляя исходные данные, получим Как видно, активная и реактивная составляющие сопротивления
Рис. 2.9
Как видно, на различных частотах значения составляющих комплексного сопротивления сильно изменяются, в том числе и характер сопротивления. Цепь на рис. 2.9а можно рассчитать через эквивалентную проводимость
вычисляя сопротивление цепи на рис. 2.9б по формуле
Очевидно, получим (2.5). Проводимость
Проведем расчет комплексной проводимости цепи на рис. 2.10а при
Рис. 2.10
В цепи имеется простое последовательное соединение двух элементов
Получим эквивалентную цепь, показанную на рис. 2.10б. Ее проводимость
Подставляя значения параметров цепи, получим
(проведите вычисления самостоятельно).
2.6. Комплексная мощность
Рис. 2.11 где ная амплитуда тока (значение
а мнимую часть
Активная мощность измеряется в ваттах (Вт), реактивная в ВАр, а комплексная в ВА. Пусть ток
(напряжение отстает по фазе от тока, сдвиг фаз между напряжением и током равен
а комплексно-сопряженная амплитуда тока - соответственно
а комплексная мощность определяется выражением
Потребляемая и реактивная мощности равны
|

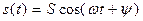 , (2.1)
, (2.1)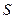 - амплитуда,
- амплитуда, 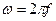 - круговая частота,
- круговая частота,  - циклическая частота,
- циклическая частота, 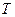 - период, а
- период, а 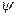 - начальная фаза.
- начальная фаза.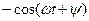
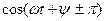

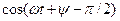
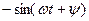
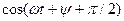
 , то после преобразования получим
, то после преобразования получим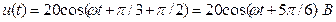
 ,
, 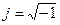 . (2.2)
. (2.2) , тогда его комплексная амплитуда равна
, тогда его комплексная амплитуда равна  . Если известна комплексная амплитуда напряжения
. Если известна комплексная амплитуда напряжения  при частоте
при частоте  , то мгновенные значения напряжения имеют вид
, то мгновенные значения напряжения имеют вид 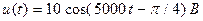 .
.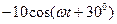
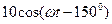
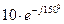
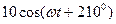


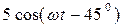
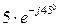
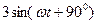
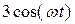
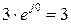
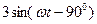
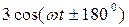
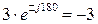
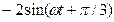
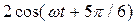
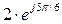

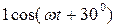
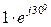
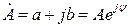 ,
, и
и 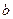 - действительная и мнимая части,
- действительная и мнимая части, ,
,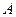 (без точки сверху) и
(без точки сверху) и 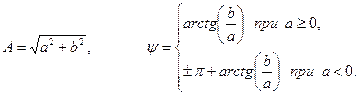
 .
.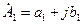 и
и 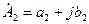 , тогда их сумма и разность соответственно равны
, тогда их сумма и разность соответственно равны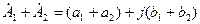 ,
,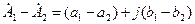 ,
,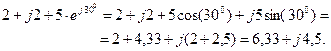
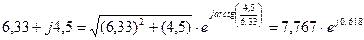 .
.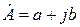
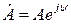
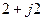
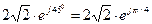

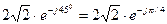
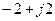
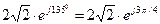

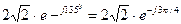
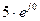
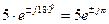

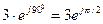
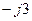


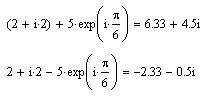
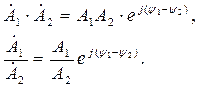
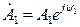

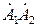
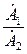
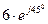

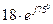
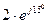

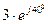
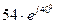


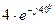

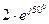
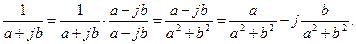
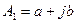 и
и  , а также
, а также 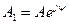 и
и 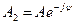 , они имеют одинаковые модули. Произведение комплексно сопряженных чисел равно квадрату их модуля
, они имеют одинаковые модули. Произведение комплексно сопряженных чисел равно квадрату их модуля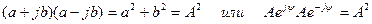 .
.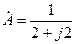

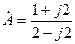
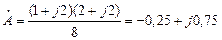
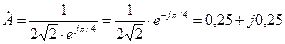
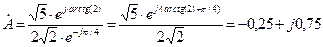

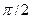 радиан), сдвиг фаз между ними
радиан), сдвиг фаз между ними 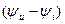 равен 900;
равен 900;
 и
и  . Поэтому построение векторной диаграммы целесообразно начинать с тока
. Поэтому построение векторной диаграммы целесообразно начинать с тока 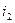 этого последовательного соединения, как показано на рис. 2.4 (вектор строится произвольно).
этого последовательного соединения, как показано на рис. 2.4 (вектор строится произвольно).
 на сопротивлении
на сопротивлении  на емкости
на емкости 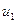 на сопротивлении
на сопротивлении 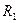 , а ток
, а ток  через
через 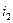 равна току источника
равна току источника 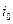 . Векторная диаграмма построена без численных расчетов (качественно). Как видно, длины векторов выбираются произвольно, за исключением тех, которые строятся по законам Кирхгофа.
. Векторная диаграмма построена без численных расчетов (качественно). Как видно, длины векторов выбираются произвольно, за исключением тех, которые строятся по законам Кирхгофа.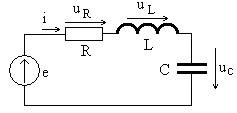
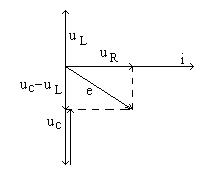 В последовательной цепи построение векторной диаграммы начинают с вектора общего тока
В последовательной цепи построение векторной диаграммы начинают с вектора общего тока 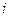 . Он отображается произвольно, например, горизонтально и направленным вправо, как показано на рис. 2.6. Напряжение на сопротивлении совпадает по фазе с током, напряжение на емкости отстает от него по фазе на 900, а напряжение на индуктивности опережает ток по фазе на 900, соответст-
. Он отображается произвольно, например, горизонтально и направленным вправо, как показано на рис. 2.6. Напряжение на сопротивлении совпадает по фазе с током, напряжение на емкости отстает от него по фазе на 900, а напряжение на индуктивности опережает ток по фазе на 900, соответст-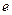 .
.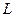 и параллельно включенные сопротивление
и параллельно включенные сопротивление 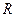 и емкость
и емкость 
 , а через емкость – опережает его по фазе на 900. Сумма токов
, а через емкость – опережает его по фазе на 900. Сумма токов 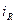 и
и 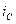 согласно первому закону Кирхгофа равна току индуктивности
согласно первому закону Кирхгофа равна току индуктивности  , а напряжение на индуктивности
, а напряжение на индуктивности 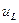 опережает ток по фазе на 900. По второму закону Кирхгофа сумма напряжений
опережает ток по фазе на 900. По второму закону Кирхгофа сумма напряжений 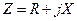 , (2.3)
, (2.3)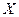 - реактивная составляющие сопротивления. Для комплексной проводимости аналогично получим
- реактивная составляющие сопротивления. Для комплексной проводимости аналогично получим , (2.4)
, (2.4)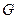 - активная, а
- активная, а 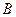 - реактивная составляющие проводимости.
- реактивная составляющие проводимости.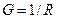
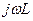
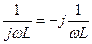
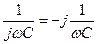
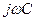
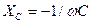 и реактивная проводимость индуктивности
и реактивная проводимость индуктивности  отрицательны,а реактивное сопротивление индуктивности
отрицательны,а реактивное сопротивление индуктивности  и реактивная проводимость емкости
и реактивная проводимость емкости  положительны. Активные сопротивление
положительны. Активные сопротивление 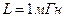 ,
, 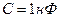 и
и 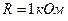 на частоте
на частоте  .
.
 которого равно
которого равно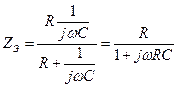 .
.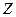 записывается в виде
записывается в виде (2.5)
(2.5)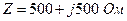 , то есть цепь имеет индуктивный характер.
, то есть цепь имеет индуктивный характер.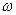 гармонического сигнала. Программа и результаты расчета этих зависимостей показаны на рис. 2.9 при
гармонического сигнала. Программа и результаты расчета этих зависимостей показаны на рис. 2.9 при  .
.
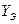 параллельного соединения элементов
параллельного соединения элементов  ,
,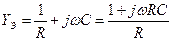 ,
,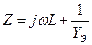 .
. цепи равна
цепи равна
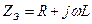 .
.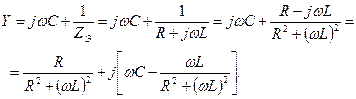
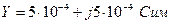 (цепь имеет емкостный характер). Сопротивление цепи равно
(цепь имеет емкостный характер). Сопротивление цепи равно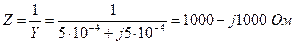
 Полная комплексная мощность гармонического воздействия на двухполюсник (рис. 2.11) с комплексными амплитудами тока
Полная комплексная мощность гармонического воздействия на двухполюсник (рис. 2.11) с комплексными амплитудами тока 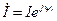 и напряжения
и напряжения 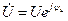 равна
равна , (2.6)
, (2.6) - комплексно-сопряжен-
- комплексно-сопряжен-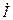 с противоположным знаком аргумента). Из (2.6) получим
с противоположным знаком аргумента). Из (2.6) получим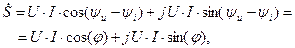 (2.7)
(2.7) - сдвиг фаз между напряжение6м и током в двухполюснике. Действительная часть
- сдвиг фаз между напряжение6м и током в двухполюснике. Действительная часть 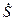 является мощностью, потребляемой цепью от источника (активной мощностью ),
является мощностью, потребляемой цепью от источника (активной мощностью ), , (2.8)
, (2.8)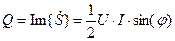 . (2.9)
. (2.9)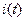 и напряжение
и напряжение  двухполюсника на рис. 2.11 представлены в виде
двухполюсника на рис. 2.11 представлены в виде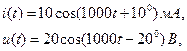
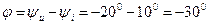 ). Комплексные амплитуды тока и напряжения соответственно равны
). Комплексные амплитуды тока и напряжения соответственно равны
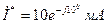 ,
,