СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ
5.1. Спектры периодических сигналов
Спектр периодического сигнала
где параметры определяются выражениями
Частота первой гармоники равна
постоянная составляющая сигнала
В выражении (5.1) Частоты гармоник
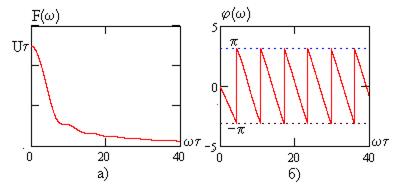
В основе расчетов спектров сигналов лежит техника интегрирования (повторите соответствующий материал) Спектры амплитуд и фаз сигнала на рис. 5.1 определены в [2] и имеют вид
График спектра амплитуд показан на рис. 5.2, а спектра фаз - а и рис. 5.2б.
Рис. 5.1
Рис. 5.2
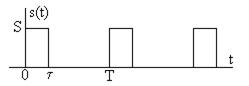
Рассмотрим сигнал, временная диаграмма которого показана на рис. 5.3.
Рис. 5.3
Как видно, он отличается от сигнала на рис. 5.1 смеще- нием (задержкой, запаздыванием) во времени на величину
Спектр амплитуд сигнала с учетом
что полностью совпадает с (5.9). Спектр фаз вычисляется по формуле
Знак минус поставлен для того, чтобы полученные значения начальных фаз После преобразований с учетом того, что
получим
и окончательно при целых значениях
На рис. 5.4а показан спектр амплитуд, на рис. 5.4б – спектр фаз, а на рис. 5.4в – временная диаграмма суммы первых сорока гармоник сигнала (рис. 5.3) при Проведем расчет спектров амплитуд и фаз сигнала на рис. 5.3 с помощью ряда Фурье в комплексной форме. Комплексная амплитуда
Рис. 5.4
Для сигнала на рис. 5.3 можно записать
С учетом (5.16) получим
Используя формулу Эйлера вида
для комплексной амплитуды получим
Не трудно убедиться, что модуль (амплитуда гармоники) и аргумент (начальная фаза гармоники) из (5.20) совпадают с (5.14) и (5.17). Проверьте это самостоятельно. Определим комплексный спектр сигнала на рис. 5.3 с помощью теоремы запаздывания. Если для сигнала
Для сигнала на рис. 5.1 комплексные амплитуды
Тогда согласно (5.21) с учетом (5.22) получим формулу (5.20). Рассмотрим спектры амплитуд и фаз сигнала, показанного на рис. 5.5.
Рис. 5.5
Расчет комплексного спектра можно провести по формуле (5.18) (проведите его самостоятельно). Для определения комплексного спектра сигнала на рис. 5.5 можно воспользоваться принципом наложения и представить его в виде суммы двух последовательностей прямоугольных импульсов
Рис. 5.6
Комплексные амплитуды гармоник сигнала
Для сигнала
или
Проведите расчет спектров амплитуд и фаз сигналов В соответствии с принципом наложения комплексные амплитуды гармоник сигнала
На рис. 5.7а показан спектр амплитуд, на рис. 5.7б – спектр фаз, а на рис. 5.7в – временная диаграмма суммы первых сорока гармоник сигнала
Рис. 5.7
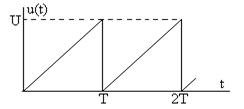
Как видно, свойство линейности, принцип наложения и теорема запаздывания позволяют существенно упростить расчеты спектров сигналов. В электронных устройствах (телевизор, осциллограф) широко используются напряжения развертки в виде последовательности пилообразных импульсов, показанной на рис. 5.8.
Рис. 5.8
Прямолинейную функцию
Определим постоянную составляющую сигнала
Найдем коэффициенты разложения сигнала в ряд Фурье. Для
Полученный интеграл вычисляется по частям,
Обозначим
и найдем
тогда
Подставляя пределы, с учетом (5.6) получим
тогда
Определим коэффициент
Проводя интегрирование по частям, получим
На рис. 5.9 показаны спектры амплитуд и фаз сигнала, а также временная реализация суммы его первых десяти гармоник.
Рис. 5.9
Проведем спектральный анализ тока
На рис 5.10 приведена программа численного расчета спектров сигнала (5.34), показаны его временная диаграмма, графики спектров амплитуд и фаз, временная диаграмма суммы первых десяти гармоник.
Рис. 5.10
Для расчетов понадобятся следующие известные из справочников по элементарной математике соотношения
Определим постоянную составляющую тока (5.34)
С учетом (5.6) вычислим коэффициент
При
Преобразуя, получим
Определим коэффициент
а при
Графики спектров амплитуд и фаз совпадают с показанными на рис. 5.10. Особенностью расчета спектра фаз является равенство нулю коэффициента Как видно из рис. 5.10, спектр амплитуд последовательности синусоидальных импульсов быстро падает с ростом номера гармоник, значимыми являются лишь первая и вторая гармоники. Временная диаграмма их суммы с постоянной составляющей показана на рис. 5.10 пунктиром. 5.2. Спектры непериодических сигналов
Прямое преобразование Фурье имеет вид
Функцию Модуль комплексной спектральной плотности
называют спектральной плотностью амплитуд сигнала. Можно использовать термин «спектр амплитуд», не забывая, что речь идет о спектральной плотности. Спектр фаз непериодического сигнала
Спектры амплитуд и фаз непериодических сигналов – непрерывные функции частоты. Для одиночного прямоугольного импульса на рис. 5.11а они определены в [2] и имеют вид
Рис. 5.11
Рассмотрим импульсный сигнал, показанный на рис. 5.11б. Из (5.41) получим
Тогда спектры амплитуд и фаз соответственно равны
Графики спектров амплитуд и фаз показаны на рис. 5.12.
Рис. 5.12
Как видно, комплексный спектр (5.47) соответствует (5.44) и теореме запаздывания (проверьте это самостоятельно).
показанного на рис. 5.13. Полная комплексная спектральная плотность сигнала может быть записана в виде Рис. 5.13
Спектр амплитуд равен
а спектр фаз соответственно
График спектра амплитуд показан на рис. 5.14.
Рис. 5.14
Исходный сигнал является четной функцией времени, поэтому в соответствии со свойствами симметрии комплексная спектральная плотность оказывается действительной функцией частоты. Определим спектр одиночного пилообразного импульса
Комплексная спектральная плот- Рис. 5.15 ность сигнала равна
Интеграл вычисляется по частям в соответствии с (5.30). Обозначим
и найдем
тогда
В результате получим
На рис. 5.16 показаны графики спектров амплитуд и фаз сигнала (рис. 5.15).
Рис. 5.14
|

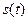 (тока или напряжения) описывается его разложением в ряд Фурье вида
(тока или напряжения) описывается его разложением в ряд Фурье вида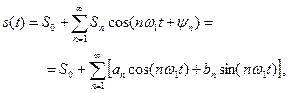 (5.1)
(5.1)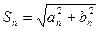 , (5.2)
, (5.2)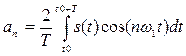 , (5.3)
, (5.3)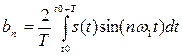 , (5.4)
, (5.4)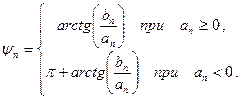 (5.5)
(5.5) , (5.6)
, (5.6)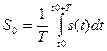 . (5.7)
. (5.7) - амплитуда
- амплитуда  -й гармоники сигнала,
-й гармоники сигнала, 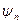 - начальная фаза
- начальная фаза 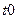 выбирается произвольно исходя из удобства расчетов.
выбирается произвольно исходя из удобства расчетов.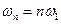 кратны частоте первой гармоники
кратны частоте первой гармоники 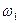 ,
, . (5.8)
. (5.8)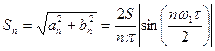 , (5.9)
, (5.9) (5.10)
(5.10)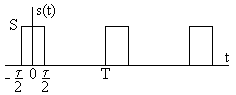

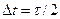 . Определим спектры амплитуд и фаз сигнала на рис. 5.3, для этого вычислим величины
. Определим спектры амплитуд и фаз сигнала на рис. 5.3, для этого вычислим величины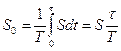 , (5.11)
, (5.11)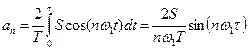 , (5.12)
, (5.12)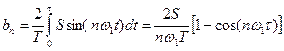 . (5.13)
. (5.13) равен
равен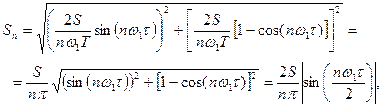 (5.14)
(5.14)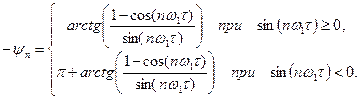 (5.15)
(5.15)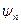 можно было использовать в формуле ряда Фурье (5.1).
можно было использовать в формуле ряда Фурье (5.1).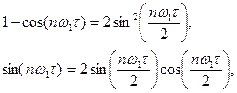 (5.16)
(5.16)

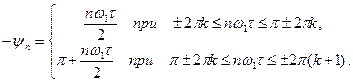 (5.17)
(5.17) ,
,  и
и  .
.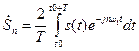 . (5.18)
. (5.18)
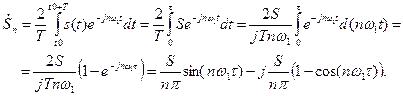
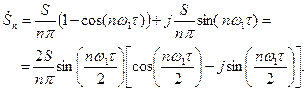
 (5.19)
(5.19)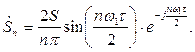 (5.20)
(5.20)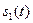 известны комплексные амплитуды
известны комплексные амплитуды 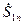
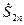 сигнала
сигнала  (задержанного на время
(задержанного на время  сигнала
сигнала 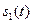 ) равен
) равен . (5.21)
. (5.21)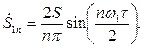 (5.22)
(5.22)
 ,
,  , показанных на рис. 5.6а и рис. 5.6б соответственно.
, показанных на рис. 5.6а и рис. 5.6б соответственно.
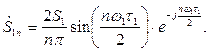 (5.23)
(5.23)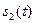 с использованием теоремы запаздывания (5.21) с учетом спектра (5.23) при длительности импульса
с использованием теоремы запаздывания (5.21) с учетом спектра (5.23) при длительности импульса  , амплитуде
, амплитуде 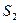 и при задержке
и при задержке  получим
получим (5.24)
(5.24)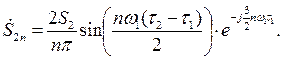 (5.25)
(5.25)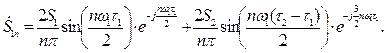 (5.26)
(5.26) ,
,  ,
,  и
и 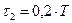 .
.
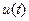 запишем в виде
запишем в виде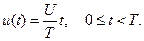 (5.27)
(5.27) . (5.28)
. (5.28)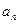 получим
получим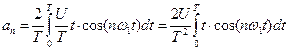 . (5.29)
. (5.29)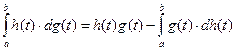 . (5.30)
. (5.30) и
и 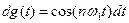 ,
, и
и 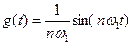 ,
,
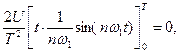
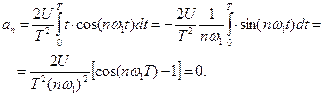 (5.31)
(5.31) ,
, , (5.32)
, (5.32)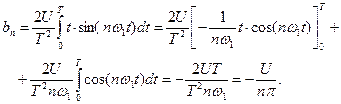 (5.33)
(5.33)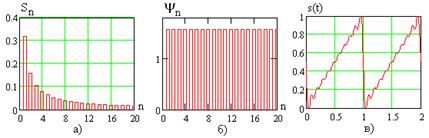
 , который возникает в выпрямителях переменного напряжения блоков питания электронной аппаратуры,
, который возникает в выпрямителях переменного напряжения блоков питания электронной аппаратуры, (5.34)
(5.34)
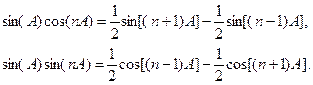 (5.35)
(5.35)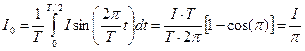 . (5.36)
. (5.36)
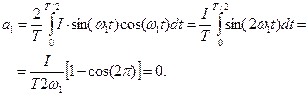 (5.37)
(5.37) аналогично
аналогично
 (5.38)
(5.38)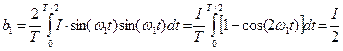 , (5.39)
, (5.39)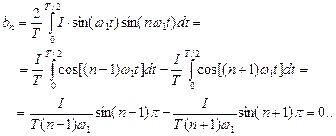 (5.40)
(5.40)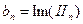 очень малы (меньше
очень малы (меньше  ), но конечны, поэтому в программе значения начальных фаз необходимо скорректировать.
), но конечны, поэтому в программе значения начальных фаз необходимо скорректировать. . (5.41)
. (5.41)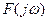 называют полной комплексной спектральной плотностью непериодического сигнала
называют полной комплексной спектральной плотностью непериодического сигнала  (5.42)
(5.42)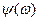 определяется выражением
определяется выражением (5.43)
(5.43)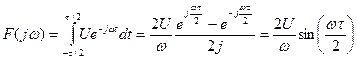 , (5.44)
, (5.44)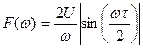 , (5.45)
, (5.45) (5.46)
(5.46)
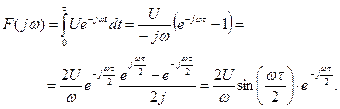 (5.47)
(5.47)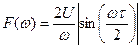 , (5.48)
, (5.48) . (5.49)
. (5.49)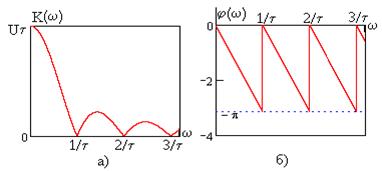
 Определим спектр экспоненциального импульса напряжения
Определим спектр экспоненциального импульса напряжения (5.50)
(5.50)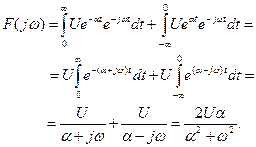 (5.51)
(5.51)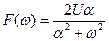 , (5.52)
, (5.52)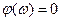 , (5.53)
, (5.53)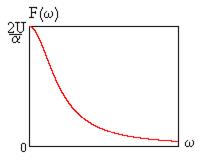
 на рис. 5.15 вида (
на рис. 5.15 вида (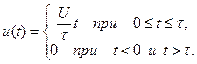 (5.54)
(5.54)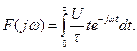
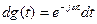 ,
, ,
,
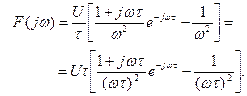 (5.55)
(5.55)