ПЕРЕХОДНЫЕ ПРОЦЕССЫ
6.1. Начальные условия
Начальные условия переходного процесса в электрической цепи это значения всех напряжений емкостей
Расчет токов и напряжений в цепи до коммутации (в стационарном режиме) ведется рассмотренными ранее методами расчета цепей постоянного тока или цепей при гармонических воздействиях. Рассмотрим цепь, показанную на рис. 6.1б.
Рис. 6.1
До коммутации ток источника был постоянным. На постоянном токе индуктивность является коротким замыканием и цепь преобразуется к виду, показанному на рис. 6.1в.
Ток
По закону коммутации (6.1) начальное условие переходного процесса имеет вид
Если все источники сигнала до коммутации выключены, как показано на рис. 6.2а, то начальные условия переходного процесса равны нулю (цепь с нулевыми начальными условиями).
Рис. 6.2
Рассмотрим цепь, показанную на рис. 6.3б.
Рис. 6.3 До коммутации в цепи в цепи действовал источник постоянного напряжения, тогда все токи и напряжения постоянны, при этом индуктивность заменяется коротким замыканием, а емкость – разрывом цепи, как показано в схеме на рис. 6.3в. Тогда ток индуктивности равен
а напряжение емкости
6.2. Классический метод расчета переходных процессов в цепях первого порядка
Запись и решение дифференциального уравнения целесообразно проводить для тока или напряжения, подчиняющегося законам коммутации, а затем можно определять искомый сигнал. Рассмотрим свободный процесс в цепи на рис. 6.4б при выключении источника тока (рис. 6.4а).
Рис. 6.4
Начальное условие (ток индуктивности После коммутации цепь принимает вид, показанный на рис. 6.4в. Общим методом расчета цепи по уравнениям Кирхгофа запишем полную систему уравнений вида
Подставляя уравнения закона Ома в последнее уравнение второго закона Кирхгофа, получим
а после преобразования запишем дифференциальное уравнение
Соответствующее ему характеристическое уравнение имеет вид
а его решение
Общее решение дифференциального уравнения (6.4) равно
где корень характеристического уравнения
Постоянная интегрирования определяется из общего решения дифференциального уравнения (6.6) и начальных условий
тогда получим
Временная диаграмма тока индуктивности показана на рис. 6.5а.
Рис. 6.5
Можно найти напряжение на индуктивности
Соответствующий график показан на рис. 6.5б. Проведем расчет свободного процесса в цепи, показанной на рис. 6.6б при выключении источника напряжения (рис. 6.6а).
Рис. 6.6
Определим начальное условие (напряжение на емкости)
тогда для напряжения
Ток
и по закону коммутации начальное условие запишется в виде
После коммутации идеальный источник напряжения выключается (заменяется коротким замыканием) и схема цепи приобретает вид, показанный на рис 6.7.
Рис. 6.7
По законам Ома и Кирхгофа составим систему уравнений электрического равновесия цепи на рис. 6.7 в виде
Из третьего и четвертого уравнений
из последнего уравнения (6.9)
тогда из второго уравнения
Из шестого уравнения
тогда из первого уравнения
Подставляя найденные токи в уравнение первого закона Кирхгофа, получим
а после преобразований запишем дифференциальное уравнение свободного процесса в канонической форме
(проведите преобразования самостоятельно). Общее решение имеет вид
где корень
равен
Для определения постоянной интегрирования используем начальное условие (6.8). Из (6.11) с учетом (6.8) получим
тогда окончательно
Зависимость напряжения на емкости от времени показана на рис. 6.8.
Рис. 6.8
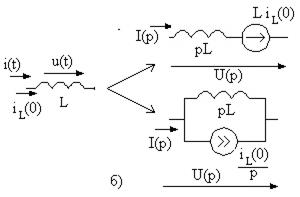
Определив напряжение на емкости, можно найти любые токи или напряжения. Проведем расчет переходного процесса в цепи на рис. 6.9 при включении источника тока. До коммутации источники сигнала в цепи отсутствовали и начальное условие
Рис. 6.9
Составим систему уравнений цепи в виде
Подставим в последнее уравнение второе и третье и получим
тогда
Подставляя результат в четвертое уравнение, получим
и после преобразований
Общее решение неоднородного дифференциального уравнения (6.15) равно сумме свободной
Свободная составляющая является решением однородного дифференциального уравнения, полученного из (6.15) обнулением правой части,
Его общее решение имеет вид
где корень характеристического уравнения
равный
тогда получим
Постоянная интегрирования определяется после расчета принужденной составляющей. Принужденную составляющую найдем двумя способами. В соответствии со справочником по математике при постоянной правой части дифференциального уравнения (6.15) принужденная составляющая также постоянна,
Подставляя (6.19) в неоднородное дифференциальное уравнение (6.15), с учетом того, что производная константы равна нулю, получим
Тогда принужденная составляющая равна
Используя закон Ома, для получим
что совпадает с (6.20) (проведите расчет самостоятельно). В результате общее решение неоднородного дифференциального уравнения (6.15) из (6.16) с учетом (6.18) и (6.20) имеет вид
Определим постоянную интегрирования. Из (6.21) при
а из начальных условий
тогда получим уравнение для постоянной интегрирования
из которого следует
Подставляя (6.22) в (6.21) получим выражение для искомого переходного процесса
или окончательно
Временная диаграмма тока индуктивности показана на рис. 6.11
Рис. 6.11
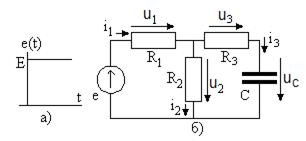
Проведем расчет переходного процесса при включении источника напряжения (рис. 6.12а) в цепи на рис. 6.12б.
Рис. 6.12
До коммутации источник напряжения был выключен и начальное условие равно нулю,
После коммутации в цепи включился источник напряжения с постоянной ЭДС
(сравните ее с (6.9)). Из третьего и четвертого уравнений (6.25)
из последнего уравнения (6.25)
тогда из второго уравнения
Из шестого уравнения
тогда из первого уравнения
Подставляя найденные токи в уравнение первого закона Кирхгофа (пятое уравнение (6.25)), получим
а после преобразований запишем неоднородное дифференциальное уравнение переходного процесса в канонической форме
(проведите алгебраические преобразования самостоятельно). Общее решение неоднородного дифференциального уравнения (6.26) является суммой свободной
Свободная составляющая переходного процесса является решением однородного дифференциального уравнения, полученного из исходного обнулением правой части,
его общее решение имеет вид
где корень
равен
Определим принужденную составляющую
тогда
С другой стороны принужденная составляющая переходного процесса равна его стационарному значению. В цепи на рис. 6.12 после коммутации действует источник постоянного напряжения, следовательно, через бесконечное время после коммутации (в стационарном режиме) все токи и напряжения в цепи станут постоянными. Эквивалентная схема цепи на постоянном токе показана на рис. 6.13.
Рис. 6.13
Напряжение на емкости (разрыве ветви) в цепи рис. 6.13 равно
что совпадает с (6.30). В результате из (6.27) с учетом (29) и (6.30) общее решение неоднородного дифференциального уравнения имеет вид
Для определения постоянной интегрирования используем начальное условие (6.24). Из (6.31) при
тогда окончательно
Временная диаграмма напряжения на емкости приведена на рис. 6.14.
Рис. 6.14
6.3. Операторный метод расчета переходных процессов в цепях первого порядка
6.3.1. Формирование операторной эквивалентной схемы цепи
Расчет переходного процесса операторным методом начинается с формирования эквивалентной операторной схемы цепи. Прежде всего, элементы цепи заменяются их операторными эквивалентами. При нулевых начальных условиях элементы заменяются эквивалентными операторными сопротивлениями в соответствии с таблицей.
Тогда операторные токи и напряжения в элементах цепи связаны классическим выражением закона Ома в виде
При ненулевых начальных условиях реактивные элементы цепи с ненулевыми начальными условиями необходимо заменить эквивалентными схемами замещения, показанными на рис. 6.15.
На рис. 6.15а показаны два варианта замены заряженной емкости (с начальным условием
Рис. 6.15
В результате необходимо изобразить графически эквивалентную операторную схему цепи с указанием положительных направлений и условных обозначений токов и напряжений. Связь между напряжениями и токами в цепи описывается законами Кирхгофа. Первый закон Кирхгофа – алгебраическая сумма операторных токов, сходящихся в узле, равна нулю,
Второй закон Кирхгофа - алгебраическая сумма операторных напряжений на элементах замкнутого контура равна алгебраической сумме операторных ЭДС включенных в контур идеальных источников напряжения,
Знаки в алгебраических суммах определяются выбранными положительными направлениями токов, напряжений, ЭДС и направлений обхода контуров.
6.3.2. Цепи с нулевыми начальными условиями
Рассмотрим цепь, показанную на рис. 6.16б при нулевых начальных условиях, и определим ток и напряжение индуктивности.
Рис. 6.16
На рис. 6.16в приведена эквивалентная операторная схема цепи, в которой обозначены операторные сопротивле- ния, положительные направления и условные обозначения токов и напряжений. По таблице преобразований Лапласа в приложении 2 изображение тока идеального источника равно
По закону Ома
для тока индуктивности
тогда для напряжения индуктивности получим
Подставим (6.36) и преобразуем результаты (6.37) и (6.37) в каноническую форму для таблицы преобразований Лапласа,
По таблице в приложении 2 находим обратное преобразование Лапласа (оригиналы тока напряжения индуктивности)
Выражение (6.41) совпадает с полученным ранее (6.11) классическим методом, график показан на рис. 6.11. Сравните сложность соответствующих расчетов. Временную диаграмму напряжения постройте самостоятельно, проверьте соотношение
Определим напряжение на емкости в цепи, показанной на рис. 6.17б при включении источника напряжения с ЭДС вида рис. 6.17а.
Рис. 6.17
Эквивалентная операторная схема цепи показана на рис. 6.17в. Операторная ЭДС
Для расчета можно использовать общий метод расчета цепи по уравнениям Кирхгофа. Полная система уравнений цепи имеет вид
Выразим из первых трех уравнений закона Ома токи ветвей и подставим их в четвертое уравнение и уравнение первого закона Кирхгофа, тогда
Выразим из первого уравнения (6.45)
Из второго уравнения (6.46) выразим
Подставив второе уравнение в первое, получим уравнение для искомого операторного напряжения емкости
найдем его в виде
и окончательно
Преобразуем (6.49) к каноническому виду для таблиц преобразования Лапласа (в знаменателе дроби сомножители с единичными коэффициентами при старшей степени
По таблице из приложения 2 получим
что совпадает с (6.32), график показан на рис. 6.14. Решим задачу (рис. 6.17) методом узловых напряжений. Эквивалентная операторная схема цепи показана на рис. 6.18. Операторная ЭДС
Рис. 6.18
Запишем уравнение метода узловых напряжений (
тогда
Для остальных ветвей используем закон Ома
Тогда из уравнения первого закона Кирхгофа
Решая (6.52), определим
Найдем искомое напряжение на емкости
Преобразуем его к каноническому виду для таблиц преобразования Лапласа (сравните с (6.50)),
По таблице из приложения 2 определим оригинал напряжения на емкости, который совпадает с (6.51). Проведите расчет самостоятельно.
6.3.3. Цепи с ненулевыми начальными условиями
При ненулевых начальных условиях соответствующие реактивные элементы заменяются эквивалентными схемами на рис. 6.15. Рассмотрим пример цепи на рис. 6.19б (ранее она рассмотрена на рис. 6.4). До коммутации в цепи действовал источник тока (рис. 6.19а) и начальное условие
Рис. 6.19
На рис. 6.19в показана эквивалентная операторная схема цепи, в которой индуктивность и ненулевым начальным током заменена ее эквивалентом согласно рис. 6.15. Определим операторный ток индуктивности в схеме на рис. 6.19в,
Из таблицы преобразования Лапласа в приложении 2 найдем оригинал тока индуктивности
что совпадает с (6.7). Определим напряжение на емкости в цепи на рис. 6.20, ранее рассмотренной на рис. 6.6.
Рис. 6.20 Начальное условие
Заменяя емкость с начальным напряжением согласно ее эквиваленту на рис. 6.15, получим операторную эквивалентную схему цепи на рис. 6.20в. Используя закон Ома, получим выражение для операторного напряжения емкости
По таблице преобразования Лапласа из приложения 2 можно записать
В результате с учетом (6.54) получим
что полностью совпадает с (6.12).
6.4. Характеристики переходных процессов
Переходные процессы протекают после коммутации и по прошествии некоторого времени переходят в установившиеся, а свободная составляющая затухает до нуля, например, как показано на рис. 6.21 для апериодического (рис. 6.21а) и колебательного (рис. 6.21б) процессов.
Рис. 6.21
Основной временной характеристикой переходного процесса является постоянная времени В цепи первого порядка могут возникать только апериодические свободные процессы (рис. 6.21а). Для поиска свободной составляющей с использованием классического метода расчета записывается дифференциальное уравнение переходного процесса и его характеристическое уравнение вида
тогда постоянная составляющая равна
При использовании операторного метода определяется изображение по Лапласу искомого сигнала вида
Тогда постоянная времени определяется выражением (6.56) В цепи второго порядка могут возникать апериодические (рис. 6.21а) и колебательные (рис. 6.21б) свободные процессы. Строго говоря, постоянная времени в этом случае находится только в колебательном режиме. При использовании классического метода расчета переходного процесса записываются его дифференциальное, а затем и характеристическое уравнения, и определяются его корни в колебательном режиме вида
где
В рамках операторного метода расчета определяется изображение по Лапласу искомого сигнала
и находятся его полюсы (корни знаменателя) вида (6.57), тогда постоянная времени равна (6.58). Рассмотрим свободный процесс в цепи на рис. 6.22б при выключении источника тока (рис. 6.22а).
Рис. 6.22
Для классического метода расчета цепь после коммутации (выключения источника) показана на рис. 6.22в и соответствующее дифференциальное уравнение имеет вид
а характеристическое уравнение
(получите их самостоятельно), тогда постоянная составляющая равна
Для операторного метода расчета эквивалентная схема цепи показана на рис. 6.22г, при этом ток индуктивности равен
тогда постоянная времени будет определяться выражением (6.59) (проведите расчет самостоятельно при Рассмотрим цепь второго порядка на рис. 6.23б при выключении источника напряжения (рис. 6.23а).
Рис. 6.23 При расчете классическим методом для схемы цепи после коммутации (рис. 6.23в) получим
и запишем характеристическое уравнение
Его корни
где
- коэффициент затухания переходного процесса,
добротность параллельного колебательного контура в параллельной эквивалентной схеме(повторите соответствующий материал). В колебательном режиме корни комплексные, то есть выполняется условие
получим
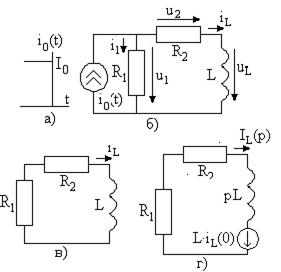
Постоянная времени обратно пропорциональна коэффициенту затухания и равна
Обратите внимание, что полученное выражение отличается от известного для последовательного колебательного контура. Проведем расчет операторным методом, операторная эквивалентная схема цепи показана на рис. 6.23г. Перестроим эквивалентную схему и получим цепь на рис. 6.24.
Рис. 6.24
Воспользуемся для расчета законом Ома. Операторный ток индуктивности
Преобразуя, получим
где
Разложим знаменатель на простые множители
где
равные (6.60). В результате постоянная времени определяется выражением (6.64). При В инженерной практике время установления
то есть для его расчета необходимо определить постоянную времени. При Декремент затухания свободного процесса равен
где
где
Рис. 6.25 Величины коэффициента затухания Например, для цепи на рис. 6.23б корни характеристического уравнения определяются выражениями (6.60) - (6.63) при
При
и из (6.67) следует
Логарифмический декремент затухания
Его расчет проводится аналогично предыдущему и для цепи на рис. 6.24б из (6.69) получим
При Логарифмический декремент затухания определяется добротностью колебательного контура
В рассматриваемом случае при
|

 и токов индуктивностей
и токов индуктивностей  в момент коммутации
в момент коммутации  (мгновенно после коммутации). Они вычисляются из тех же значений напряжений и токов непосредственно до коммутации (
(мгновенно после коммутации). Они вычисляются из тех же значений напряжений и токов непосредственно до коммутации ( ) на основе законов коммутации
) на основе законов коммутации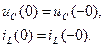 (6.1)
(6.1)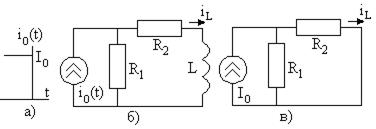
 в цепи рис.6.1в равен (проведите расчет цепи постоянного тока с помощью закона Ома самостоятельно)
в цепи рис.6.1в равен (проведите расчет цепи постоянного тока с помощью закона Ома самостоятельно) .
. . (6.2)
. (6.2)

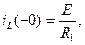
 , так как ветвь с последовательно соединенными емкостью
, так как ветвь с последовательно соединенными емкостью  и сопротивлением
и сопротивлением 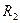 замкнута и напряжение на ней равно нулю.
замкнута и напряжение на ней равно нулю.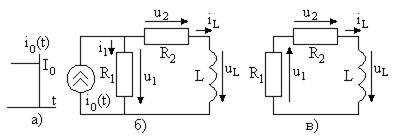

 (6.3)
(6.3) ,
,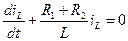 . (6.4)
. (6.4) ,
, . (6.5)
. (6.5)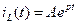 ,
,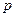 определяется (6.5). Подставляя (6.5), получим
определяется (6.5). Подставляя (6.5), получим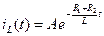 . (6.6)
. (6.6) ,
,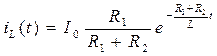 . (6.7)
. (6.7)
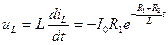 ,
,
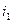 равен
равен ,
,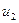 получим
получим .
. в разрыве цепи отсутствует, напряжение
в разрыве цепи отсутствует, напряжение  равно нулю, тогда напряжение на емкости равно
равно нулю, тогда напряжение на емкости равно
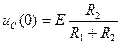 . (6.8)
. (6.8)
 (6.9)
(6.9) ,
, ,
,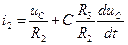 .
. ,
, .
. ,
, (6.10)
(6.10) , (6.11)
, (6.11)
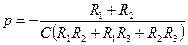 .
.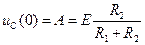 ,
,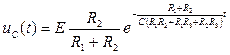 . (6.12)
. (6.12)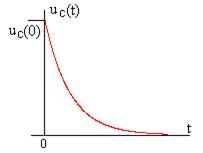
 . (6.13)
. (6.13)
 (6.14)
(6.14) ,
,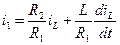 .
.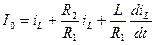
 . (6.15)
. (6.15) и принужденной
и принужденной 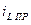 составляющих имеет вид
составляющих имеет вид . (6.16)
. (6.16) . (6.17)
. (6.17) ,
,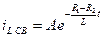 . (6.18)
. (6.18) . (6.19)
. (6.19)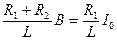 .
. . (6.20)
. (6.20) С другой стороны [3], принужденная составляющая является стационарным процессом в цепи (через бесконечное время после коммутации). В рассматриваемой цепи (рис. 6.9) после коммутации действует источник постоянного тока, поэтому стационарные токи и напряжения будут постоянными и эквивалентная схема цепи в стационарном режиме примет вид, показанный на рис. 6.10 (индуктивность на постоянном токе заменяется коротким замыканием). Рис. 6.10
С другой стороны [3], принужденная составляющая является стационарным процессом в цепи (через бесконечное время после коммутации). В рассматриваемой цепи (рис. 6.9) после коммутации действует источник постоянного тока, поэтому стационарные токи и напряжения будут постоянными и эквивалентная схема цепи в стационарном режиме примет вид, показанный на рис. 6.10 (индуктивность на постоянном токе заменяется коротким замыканием). Рис. 6.10 ,
,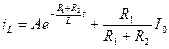 . (6.21)
. (6.21) ,
, ,
,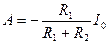 . (6.22)
. (6.22) ,
,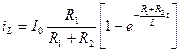 . (6.23)
. (6.23)
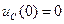 . (6.24)
. (6.24)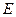 . На основе законов Ома и Кирхгофа для мгновенных значений сигналов запишем систему уравнений
. На основе законов Ома и Кирхгофа для мгновенных значений сигналов запишем систему уравнений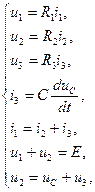 (6.25)
(6.25) ,
,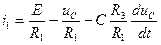 .
. ,
,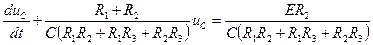 (6.26)
(6.26)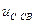 и принужденной
и принужденной 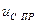 составляющих
составляющих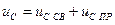 . (6.27)
. (6.27) , (6.28)
, (6.28) , (6.29)
, (6.29) . Подставляя ее в (6.26) получим
. Подставляя ее в (6.26) получим ,
, . (6.30)
. (6.30)
 ,
,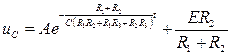 . (6.31)
. (6.31) или
или 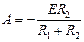 ,
, . (6.32)
. (6.32)


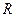





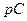
 или
или  . (6.33)
. (6.33)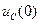 ) с идеальными источниками напряжения или тока. На рис. 6.15б показаны два варианта замены индуктивности с начальным условием
) с идеальными источниками напряжения или тока. На рис. 6.15б показаны два варианта замены индуктивности с начальным условием  с идеальными источниками напряжения или тока.
с идеальными источниками напряжения или тока.
 . (6.34)
. (6.34) . (6.35)
. (6.35)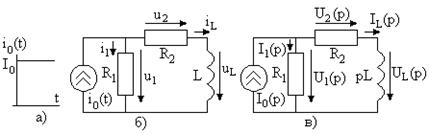
 . (6.36)
. (6.36) ,
,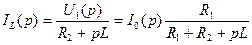 , (6.37)
, (6.37) . (6.38)
. (6.38) , (6.39)
, (6.39) . (6.40)
. (6.40) , (6.41)
, (6.41)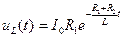 . (6.42)
. (6.42)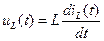 .
.
 источника определяется из таблицы в приложении 2 и равна
источника определяется из таблицы в приложении 2 и равна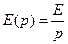 . (6.43)
. (6.43)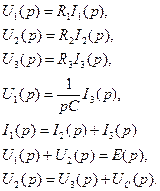 (6.44)
(6.44)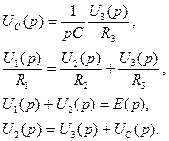 (6.45)
(6.45)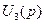 и поставим его во второе и четвертое, в результате запишем
и поставим его во второе и четвертое, в результате запишем (6.46)
(6.46) и подставим его в первое, тогда
и подставим его в первое, тогда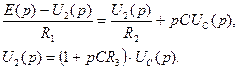 (6.47)
(6.47)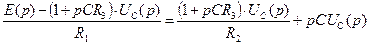 , (6.48)
, (6.48)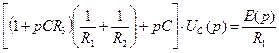
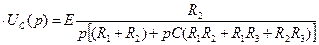 . (6.49)
. (6.49)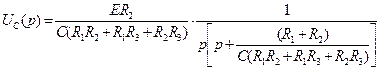 . (6.50)
. (6.50)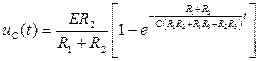 , (6.51)
, (6.51)
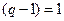 ). Для этого обозначим узловое напряжение
). Для этого обозначим узловое напряжение  и выразим через него токи всех ветвей. Для контура с источником напряжения по второму закону Кирхгофа
и выразим через него токи всех ветвей. Для контура с источником напряжения по второму закону Кирхгофа ,
, .
.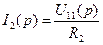
 .
. получим уравнение метода узловых напряжений в виде
получим уравнение метода узловых напряжений в виде . (6.52)
. (6.52)



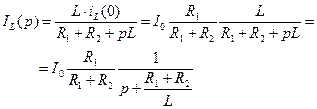
 . (6.53)
. (6.53)
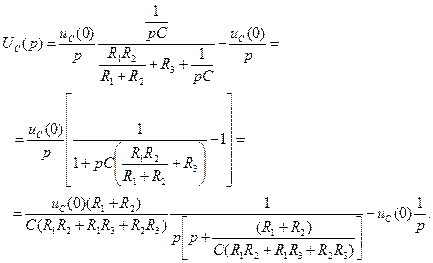

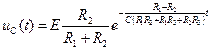 , (6.55)
, (6.55)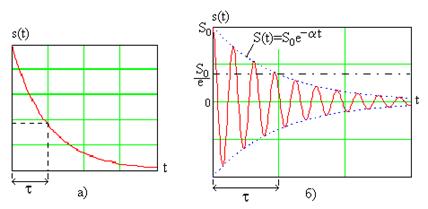
 - интервал времени, в течение которого свободная составляющая переходного процесса в апериодическом режиме (рис. 6.21а) или его амплитуда в колебательном режиме (рис. 6.21б) уменьшаются в
- интервал времени, в течение которого свободная составляющая переходного процесса в апериодическом режиме (рис. 6.21а) или его амплитуда в колебательном режиме (рис. 6.21б) уменьшаются в  раза от исходного значения.
раза от исходного значения. ,
, . (6.56)
. (6.56) или
или  ,
,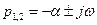 , (6.57)
, (6.57)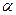 - коэффициент затухания, а
- коэффициент затухания, а 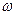 - частота свободных колебаний. Тогда постоянная времени цепи равна
- частота свободных колебаний. Тогда постоянная времени цепи равна . (6.58)
. (6.58) или
или 
 ,
,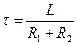 . (6.59)
. (6.59)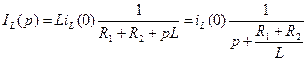 ,
, и
и  ).
).
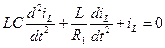
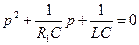 .
. и
и  имеют вид
имеют вид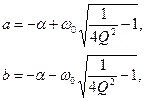 (6.60)
(6.60)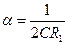 (6.61)
(6.61)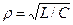 - характеристическое сопротивление параллельного колебательного контура,
- характеристическое сопротивление параллельного колебательного контура, 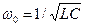 - его резонансная частота,
- его резонансная частота,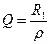
 (получите его самостоятельно), тогда обозначив частоту свободных колебаний
(получите его самостоятельно), тогда обозначив частоту свободных колебаний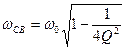 , (6.62)
, (6.62) (6.63)
(6.63)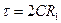 . (6.64)
. (6.64)
 равен
равен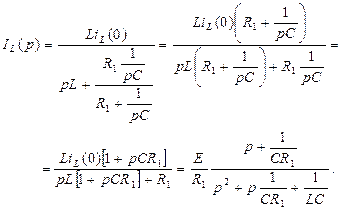
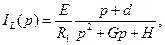
 ,
, 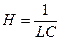 ,
,  ,
,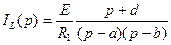 ,
, ,
,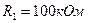 ,
,  и
и 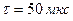 .
. переходного процесса принимается равным
переходного процесса принимается равным , (6.65)
, (6.65)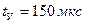 .
.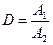 , (6.66)
, (6.66) и
и 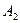 - значение амплитуд свободных колебаний, разделенных одним периодом (рис. 6.25). Его можно определить по формуле
- значение амплитуд свободных колебаний, разделенных одним периодом (рис. 6.25). Его можно определить по формуле , (6.67)
, (6.67) -рассмотренный выше коэффициент затухания, а
-рассмотренный выше коэффициент затухания, а  - период свободных колебаний,
- период свободных колебаний, . (6.68)
. (6.68) - частота свободных колебаний.
- частота свободных колебаний.
 (полюсов операторного тока или напряжения) в колебательном режиме.
(полюсов операторного тока или напряжения) в колебательном режиме. , тогда
, тогда (6.69)
(6.69) ,
, ,
, ,
,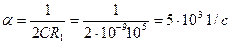 ,
, .
. равен
равен . (6.70)
. (6.70) . (6.71)
. (6.71)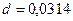 (проведите расчет самостоятельно).
(проведите расчет самостоятельно).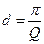 , (6.72)
, (6.72)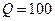 получим то же значение
получим то же значение 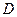 и затем ег
и затем ег


