Положительные направления
(стрелками) и условные обозначения всех токов и напряжений для всех элементов цепи. В данном случае ток Общее сопротивление цепи относительно клемм источника (сопротивление двух последовательно соединенных элементов
Для напряжений на элементах получим
Для проверки воспользуемся вторым законом Кирхгофа в виде
(убедитесь в правильности полученных результатов).
Рис. 1.2 на них одинаковы и равны
Примем В цепи источника протекает ток
тогда общее напряжение равно
Токи в ветвях
Для проверки воспользуемся уравнением первого закона Кирхгофа в виде
(убедитесь в правильности полученных результатов). Рассмотрим более сложную цепь на рис. 1.3, в которой присутствует смешанное соединение ветвей
Рис. 1.3
Параметры цепи выберем равными В смешанной цепи выделяем фрагмент с простым параллельным соединением элементов
Этот фрагмент подключен к
Рис. 1.4 Общий ток в цепи
тогда определим напряжение на элементе
Напряжение на параллельном соединении сопротивлений
Для проверки убедитесь в выполнении второго закона Кирхгофа,
Определим токи в элементах
Убедитесь в выполнении уравнения первого закона Кирхгофа
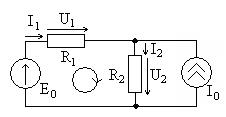
Рассмотрим пример расчета цепи с источником тока, схема которой приведена на рис. 1.5, при токе идеального источника
ных сопротивлений Рис. 1.5
Тогда напряжение
Затем можно найти токи ветвей
Полученные результаты можно проверить с помощью первого закона Кирхгофа в виде Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина
По второму закону Кирхгофа
1.3. Общий метод расчета цепи на основе законов Ома и Кирхгофа
Общий метод расчета токов и напряжений в электрической цепи на основе законов Ома и Кирхгофа пригоден для расчета сложных цепей с несколькими источниками сигнала. Расчет начинается с задания обозначений и положительных направлений токов и напряжений для каждого элемента (сопротивления) цепи. Система уравнений включает в себя подсистему компонентных уравнений, связывающих по закону Ома токи и напряжения в каждом элементе (сопротивлении) и подсистему топологических уравнений, построенную на основе первого и второго законов Кирхгофа. По первому закону Кирхгофа записывается По второму закону Кирхгофа записываются Рассчитаем токи и напряжения в простой цепи на рис. 1.3 при тех же исходных данных. В цепи имеется два узла ( (
Рис. 1.6
Запишем подсистему компонентных уравнений
По первому закону Кирхгофа необходимо записать одно уравнение (
и два уравнения по второму закону Кирхгофа (
которые образуют подсистему топологических уравнений. Объединяя полученные уравнения в систему и подставляя (1.2) в (1.4), получим систему уравнений для токов ветвей
Из первого уравнения ток
Из второго уравнения (1.6) выразим ток
и подставив его в первое уравнение, получим
Из (1.8) определим ток
Подставляя (1.9) в (1.7), найдем ток
и из (1.3) получим ток
Подставляя в (1.9)-(1.11) исходные данные
Рис. 1.7
Систему уравнений (1.5) можно решить по правилу Крамера с использованием определителей (приложение 1 ). Для этого запишем ее в каноническом виде
Детерминант (определитель) системы равен
и положителен, то есть система уравнений имеет единственное решение, равное
где
В результате для токов ветвей получим
Что полностью совпадает с полученными методом подстановки результатами. Для расчетов определителей и решения системы уравнений можно воспользоваться пакетом MathCAD, листинг программы показан на рис. 1.8. Как видно, получены те же результаты.
Рис. 1.8
Подсистема компонентных уравнений на базе закона Ома для каждого эле- Рис. 1.9 мента цепи имеет вид
В цепи имеется два узла (
жащие идеальных источников тока (
и одно уравнение второго закона Кирхгофа (
которые и образуют подсистему топологических уравнений. Уравнения (1.12) - (1.14) являются полной системой уравнений цепи. Подставляя (1.12) в (1.14), получим
а, объединив (1.13) и (1.15), получим два уравнения с двумя неизвестными токами ветвей,
Выражая из первого уравнения (1.16) ток
а затем найдем Рассмотрим цепь с двумя источниками сигнала, показанную на рис. 1.10 при
Рис. 1.10
Подсистема компонентных уравнений имеет вид
В цепи имеется два узла (
и одно уравнение второго закона Кирхгофа (
Подставляя (1.17) в (1.19), получим систему уравнений для токов цепи
Ток
из которого найдем ток
Подставляя исходные данные, получим
А из первого уравнения (1.20) соответственно
Напряжения на элементах согласно (1.17) равны
Проверьте выполнимость первого и второго законов Кирхгофа для полученных результатов. Проведите аналогичный расчет при
1.4. Метод контурных токов
Метод контурных токовбазируется науравнениях второго закона Кирхгофа [1] и приводит к необходимости решения В цепи выбираются
Рис. 1.11 Через ветвь
В ветви
Для контуров, не содержащих идеальные источники тока, составляем уравнения второго закона Кирхгофа с использованием закона Ома, в данном примере записывается одно уравнение
Если в контур включен идеальный источник тока, то для него уравнение второго закона Кирхгофа не составляется, а его контурный ток равен току источника с учетом их положительных направлений, в рассматриваемом случае
Тогда система уравнений метода контурных токов принимает вид
В результате подстановки второго уравнения в первое из (1.27) получим
тогда ток
а ток
Проведем расчет токов и напряжений в цепи, показанной на рис. 1.12 при
Рис. 1.12
В цепи два узла Выразим токи ветвей через контурные токи,
а через них найдем напряжения на элементах,
Записав уравнения второго закона Кирхгофа,
и подставив в них (1.31), получим уравнения метода контурных токов в виде
Из первого уравнения (1.32) выразим ток
и подставим его во второе, тогда получим выражение
из которого определим ток
Из (1.33) найдем ток
Подставляя исходные данные, из (1.34) и (1.35) получим значения контурных токов Проведем расчет токов и напряжений в цепи на рис.1.10 методом контурных токов, как показано на рис. 1.13, при следующих исходных данных:
Рис. 1.13
В цепи два узла и три ветви, тогда необходимо ввести два контурных тока (рис. 1.13). Ток
тогда для первого контура по второму закону Кирхгофа и закону Ома получим
В результате получим систему уравнений по методу контурных токов в виде
Подставляя второе уравнение в первое, получим
и найдем ток
Подставляя исходные данные, получим
Напряжения на элементах вычислите самостоятельно, сравните результаты с полученными ранее для цепи на рис. 1.9.
1.5. Метод узловых напряжений
Метод узловых напряжений базируется на первом законе Кирхгофа [1], при этом число уравнений равно В цепи выделяются все
Рис. 1.14 как по закону Ома токи ветвей
По первому закону Кирхгофа с учетом (1.39) запишем единственное (
Решая его, получим
а из (1.39) определим токи ветвей
Результаты совпадают с полученными рассмотренными ранее методами (проведите численные вычисления самостоятельно). Проведем расчет токов и напряжений в цепи, показанной на рис. 1.3 при
Рис. 1.15
Выразим через
откуда получим
В сопротивлениях
По первому закону Кирхгофа для цепи рис. 1.14 записывается одно уравнение вида
Подставляя в него (1.43) и (1.44), получим уравнение метода узловых напряжений
Решая (1.45) определим узловое напряжение
Подставляя исходные данные, получим По найденному значению
Сравните их с полученными ранее результатами. Проведем расчет цепи на рис. 1.16 (ранее он проводился для цепи на рис. 1.10) при
Рис. 1.16
Выберем базисным нижний узел и обозначим узловое напряжение
Найдем ток
Запишем уравнение первого закона Кирхгофа
Тогда с учетом (1.47) и (1.48) получим уравнение метода узловых напряжений
Решая его, найдем узловое напряжение
Подставляя исходные данные, получим Рассмотрим более сложный пример цепи, показанной на рис. 1.17 с параметрами
Рис. 1.17
Введены положительные направления и обозначения токов и напряжений ветвей и узловых напряжений Выразим напряжения на элементах цепи через узловые напряжения, используя второй закон Кирхгофа,
По закону Ома определим токи ветвей,
По первому закону Кирхгофа для узлов с номерами 1 и 2 необходимо составить два уравнения,
Подставляя (1.51) в (1.52), получим систему уравнений метода узловых напряжений,
После преобразования получим
Выразив из второго уравнения (1.54)
из первого уравнения найдем
Подставляя исходные данные, из (1.56) получим Программа расчета узловых напряжений и токов ветвей приведена на рис. 1.18. Там же проведено численное решение системы уравнений, определены токи ветвей и проведена проверка полученных результатов с помощью законов Кирхгофа. Повторите проведенные расчеты и определите напряжения на элементах цепи.
Рис. 1.18
1.6. Метод наложения
Метод наложения заключается в следующем: реакция цепи (ток или напряжение) на воздействие нескольких источников равна сумме реакций на действие каждого из них в отдельности, при этом остальные источники должны быть выключены [1]. Выключение идеальных источников означает замену: - идеального источника напряжения коротким замыканием, так как его внутреннее сопротивление равно нулю; - идеального источника тока холостым ходом (разрывом цепи) так как его внутреннее сопротивление стремится к бесконечности. Расчет проводится следующим образом. В цепи, содержащей несколько источников, поочередно выбирается каждый из них, а остальные отключаются. При этом образуются цепи с одним источником, число которых равно количеству источников в исходной цепи. В каждой из них проводится расчет искомого сигнала, а результирующий сигнал определяется их суммой. Проведем расчет цепи на рис. 1.19 при
Рис. 1.19
Выключим идеальный источник тока (заменим его разрывом цепи) и получим цепь, показанную на рис. 1.20а.
Рис. 1.20
По закону Ома определим ток
тогда напряжения
Выключим идеальный источник напряжения (заменим его коротким замыканием) и получим схему, показанную на рис. 1.20б. По закону Ома в соответствии с выбранными положительными направлениями определим напряжения
а токи ветвей соответственно равны
Складывая реакции цепи (токи и напряжения) со штрихом и двумя штрихами, получим искомые значения
Подставьте исходные данные и получите численные результаты, сравните их с полученными ранее. Проверьте выполнимость законов Кирхгофа
В цепи, показанной на рис. 1.21 (ранее она рассматривалась на рис. 1.17) с параметрами
Рис. 1.21
Рис. 1.22
С помощью закона Ома в цепи рис. 1.22а определим напряжение
(проведите расчет самостоятельно). Аналогично в цепи на рис. 1.22б найдем напряжение
а затем напряжение
Подставляя
Сложив
Подставляя исходные данные, получим
|

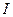 в последовательно соединенных сопротивлениях одинаков.
в последовательно соединенных сопротивлениях одинаков.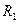 и
и 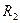 ) равно сумме их сопротивлений, тогда по закону Ома общий ток в цепи
) равно сумме их сопротивлений, тогда по закону Ома общий ток в цепи 
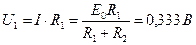 ,
,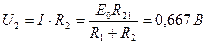 .
.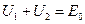 ,
, Рассмотрим цепь с идеальным источником тока, показанную на рис. 1.2. Зададим положительные направления и условные обозначения токов и напряжений (элементы
Рассмотрим цепь с идеальным источником тока, показанную на рис. 1.2. Зададим положительные направления и условные обозначения токов и напряжений (элементы  ).
). ,
, 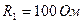 и
и  .
. , а к источнику тока подключены параллельно соединенные элементы
, а к источнику тока подключены параллельно соединенные элементы  ,
, .
.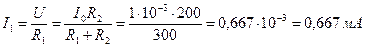 ,
,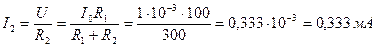 .
.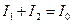
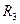 . Элементы
. Элементы 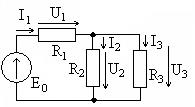
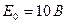 ,
, 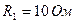 ,
, 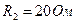 и
и 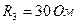 . Введем положительные направления и условные обозначения токов и напряжений (рис. 1.3).
. Введем положительные направления и условные обозначения токов и напряжений (рис. 1.3). .
.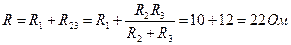 .
.
 по закону Ома равен
по закону Ома равен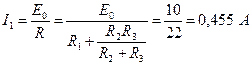 ,
,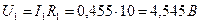 .
.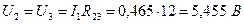 .
. ,
, .
. .
. А и сопротивлениях
А и сопротивлениях 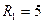 Ом,
Ом,  Ом,
Ом,  Ом. Необходимо определить токи ветвей
Ом. Необходимо определить токи ветвей  и
и 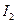 , а также напряжения на сопротивлениях
, а также напряжения на сопротивлениях 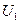 ,
,  и
и  .
.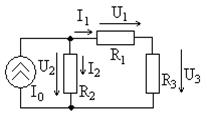 Вычислим общее сопротивление цепи
Вычислим общее сопротивление цепи 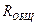 относительно зажимов источника тока (параллельного соединения сопротивления
относительно зажимов источника тока (параллельного соединения сопротивления  и последовательно соединен-
и последовательно соединен- и
и 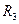 ),
), .
. В.
В.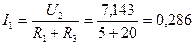 А,
А, А.
А. .
. В,
В, В.
В.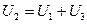 (проведите проверку самостоятельно).
(проведите проверку самостоятельно). уравнений, где
уравнений, где 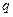 - число узлов в цепи.
- число узлов в цепи.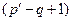 уравнений, где
уравнений, где 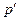 - число ветвей в цепи, не содержащих идеальные источники тока.
- число ветвей в цепи, не содержащих идеальные источники тока. ) и три ветви, не содержащие идеальных источников тока (
) и три ветви, не содержащие идеальных источников тока ( ), то есть имеем два
), то есть имеем два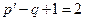 ) независимых контура. Обозначим положительные направления обхода контуров (рис. 1.6).
) независимых контура. Обозначим положительные направления обхода контуров (рис. 1.6).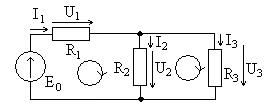
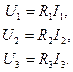 (1.2)
(1.2)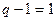 ),
), , (1.4)
, (1.4)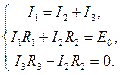 (1.5)
(1.5) (1.6)
(1.6) ,
, , (1.7)
, (1.7) . (1.8)
. (1.8) . (1.9)
. (1.9) , (1.10)
, (1.10) , (1.11)
, (1.11) А,
А,  А и
А и  А, что совпадает с результатами расчета для цепи на рис. 1.3. Напряжения на элементах определяются из компонентных уравнений (1.2). На рис. 1.7 приведен листинг программы расчета токов и напряжений.
А, что совпадает с результатами расчета для цепи на рис. 1.3. Напряжения на элементах определяются из компонентных уравнений (1.2). На рис. 1.7 приведен листинг программы расчета токов и напряжений.

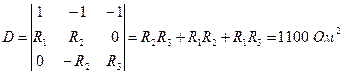
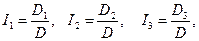
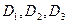 - определители, получающиеся из детерминанта заменой
- определители, получающиеся из детерминанта заменой  -го столбца (
-го столбца (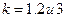 ) столбцом из свободных членов системы уравнений,
) столбцом из свободных членов системы уравнений,
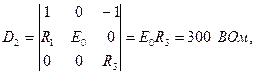



 Рассмотрим расчет цепи, показанной на рис. 1.5, при тех же исходных данных. Схема цепи с указанным направлением обхода контура приведена на рис. 1.9.
Рассмотрим расчет цепи, показанной на рис. 1.5, при тех же исходных данных. Схема цепи с указанным направлением обхода контура приведена на рис. 1.9.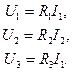 (1.12)
(1.12)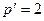 ). Следовательно, необходимо записать одно уравнение (
). Следовательно, необходимо записать одно уравнение (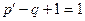 ),
),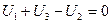 , (1.14)
, (1.14)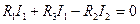 , (1.15)
, (1.15)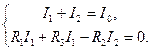 (1.16)
(1.16)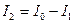 и подставляя его во второе, найдем значение тока
и подставляя его во второе, найдем значение тока  А,
А, А. По вычисленным токам ветвей из компонентных уравнений (1.12) определим напряжения. Результаты расчета совпадают с полученными ранее для цепи на рис. 1.5.
А. По вычисленным токам ветвей из компонентных уравнений (1.12) определим напряжения. Результаты расчета совпадают с полученными ранее для цепи на рис. 1.5.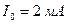 ,
, 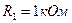 ,
,  .
.
 (1.17)
(1.17)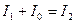 , (1.18)
, (1.18)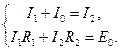 (1.20)
(1.20) из первого уравнения (1.20) подставим во второе, тогда получим уравнение
из первого уравнения (1.20) подставим во второе, тогда получим уравнение , (1.21)
, (1.21)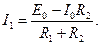 (1.22)
(1.22) ,
, .
.
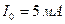 ,
,  , объясните полученные результаты.
, объясните полученные результаты. уравнений,
уравнений, 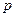 - число всех ветвей, в том числе и содержащих идеальные источники тока.
- число всех ветвей, в том числе и содержащих идеальные источники тока. -го из них вводится кольцевой (замкнутый) контурный ток
-го из них вводится кольцевой (замкнутый) контурный ток 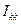 (двойная индексация позволяет отличать контурные токи от токов ветвей). Через контурные токи можно выразить все токи ветвей и для каждого независимого контура записать уравнения второго закона Кирхгофа. Система содержит
(двойная индексация позволяет отличать контурные токи от токов ветвей). Через контурные токи можно выразить все токи ветвей и для каждого независимого контура записать уравнения второго закона Кирхгофа. Система содержит  Рассмотрим пример цепи на рис. 1.5 при
Рассмотрим пример цепи на рис. 1.5 при 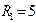 Ом,
Ом, 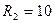 Ом,
Ом,  и
и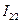 (
(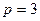 ,
, 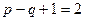 ).
). протекает только контурный ток
протекает только контурный ток 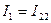 . (1.23)
. (1.23) . (1.24)
. (1.24) . (1.25)
. (1.25) . (1.26)
. (1.26) . (1.27)
. (1.27) , (1.28)
, (1.28) А, (1.29)
А, (1.29) А. Из (1.23)
А. Из (1.23) 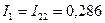 А, а из (1.24) соответственно
А, а из (1.24) соответственно 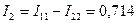 А, что полностью совпадает с полученными ранее результатами. По найденным значениям токов ветвей по закону Ома вычислим напряжения на элементах цепи рис. 1.5,
А, что полностью совпадает с полученными ранее результатами. По найденным значениям токов ветвей по закону Ома вычислим напряжения на элементах цепи рис. 1.5,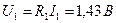 ,
,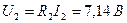 ,
,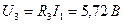 .
.
 и три ветви
и три ветви 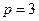 , тогда по второму закону Кирхгофа с учетом закона Ома необходимо составить два уравнения (
, тогда по второму закону Кирхгофа с учетом закона Ома необходимо составить два уравнения (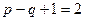 ) метода контурных токов,
) метода контурных токов, (1.30)
(1.30) (1.31)
(1.31)
 (1.32)
(1.32)
 (1.33)
(1.33)
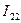 ,
,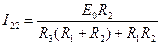 . (1.34)
. (1.34) . (1.35)
. (1.35) и
и  , тогда из (1.30) определим токи ветвей
, тогда из (1.30) определим токи ветвей 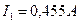 ,
, 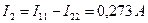 и
и  . Напряжения ветвей определяются из (1.31):
. Напряжения ветвей определяются из (1.31): 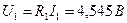 ,
, 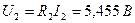 и
и  . Результаты совпадают с полученными ранее для цепи на рис. 1.3.
. Результаты совпадают с полученными ранее для цепи на рис. 1.3. ,
, 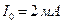 ,
,  ,
, 
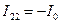 . Выразим токи ветвей через контурные токи,
. Выразим токи ветвей через контурные токи,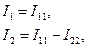 (1.36)
(1.36)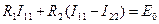 .
. (1.37)
(1.37)
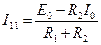 . (1.38)
. (1.38) , тогда из (1.36) найдем токи ветвей
, тогда из (1.36) найдем токи ветвей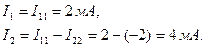
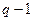 .
. …
… 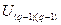 остальных
остальных 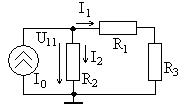 Рассмотрим пример цепи, показанной рис. 1.5 при
Рассмотрим пример цепи, показанной рис. 1.5 при 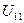 . Выразим через него
. Выразим через него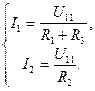 (1.39)
(1.39) . (1.40)
. (1.40) ,
,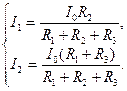 (1.41)
(1.41)
 , (1.42)
, (1.42) . (1.43)
. (1.43)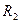 и
и  токи определяются по закону Ома,
токи определяются по закону Ома, (1.44)
(1.44)
 . (1.45)
. (1.45)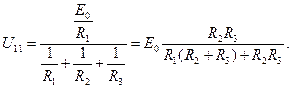 (1.46)
(1.46) .
.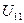 вычислим токи и напряжения в цепи:
вычислим токи и напряжения в цепи:
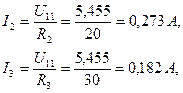

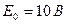 ,
,  ,
,  ,
, 
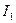 (это уже делалось в (1.42) и (1.43)),
(это уже делалось в (1.42) и (1.43)), ,
,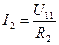 . (1.48)
. (1.48)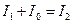 ,
,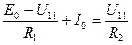 . (1.49)
. (1.49) . (1.50)
. (1.50) , тогда из (1.47)
, тогда из (1.47) 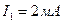 и из (1.48)
и из (1.48)  ,
, 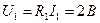 и
и 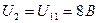 (сравните самостоятельно с предыдущими результатами).
(сравните самостоятельно с предыдущими результатами). ,
, 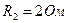 ,
,  ,
,  ,
, 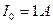 . В цепи
. В цепи  узла, нижний выбран базисным, а два остальные обозначены номерами в кружках.
узла, нижний выбран базисным, а два остальные обозначены номерами в кружках.
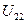 .
.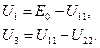
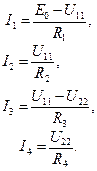 (1.51)
(1.51)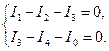 (1.52)
(1.52)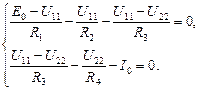 (1.53)
(1.53)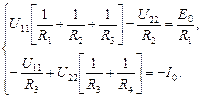 (1.54)
(1.54) , (1.55)
, (1.55)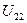
 . (1.56)
. (1.56) и из (1.55)
и из (1.55) 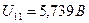 .
.
 ,
, 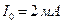 ,
, 
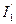
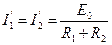 ,
,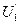 и
и 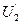 равны
равны
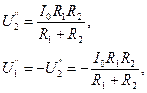




 на сопротивлении
на сопротивлении 


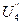 на сопротивлении
на сопротивлении  ,
,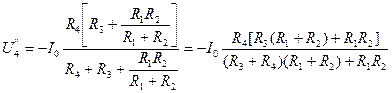 ,
, ,
, .
. .
.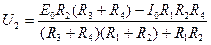 .
.


