РАСЧЕТ ЧАСТОТНО-СЕЛЕКТИВНЫХ ЦЕПЕЙ
4.1. Входные и выходные сопротивления и проводимости четырехполюсника
Свойства четырехполюсника с точки зрения источника сигнала и нагрузки (рис. 4.1) описываются его входными
Рис. 4.1
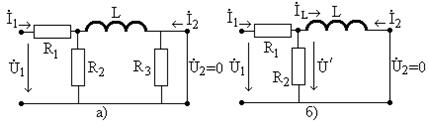
На рис. 4.2а показаны эквивалентные схемы входной, а на рис. 4.2б - выходной цепей четырехполюсника.
Рис. 4.2
На рис. 4.2 обозначено:
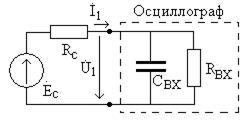
Рассмотрим схему (рис. 4.3), возникающую при измерении сигнала реального источника напряжения с помощью осциллографа, входная цепь которого представляет собой параллельное соединение сопротивления
Рис. 4.3
Входное сопротивление
Входное сопротивление имеет активную
Модуль входного сопротивления осциллографа равен
На рис. 4.4 показаны зависимости сопротивлений от частоты.
Рис. 4.4
Как видно, модуль и активная составляющая входного сопротивления осциллографа падают с увеличением частоты, это проявляется на частотах выше
Если с помощью осциллографа измеряется амплитуда ЭДС (напряжения) источника
Амплитуда
Зависимость от частоты нормированных напряжений
Рис. 4.5
В общем случае входное сопротивление четырехполюсника зависит от сопротивления нагрузки. Устранить это влияние можно включением между источником сигнала и нагрузкой усилителей сигнала. Рассмотрим нагруженный пассивный четырехполюсник, схема которого показана на рис. 4.6.
Рис. 4.6
Входное сопротивление равно
После преобразований получим
Проведите анализ входного сопротивления и его составляющих, постройте графики. Рассмотрим влияние выходного (внутреннего) сопротивления четырехполюсника на выходную цепь (рис. 4.2б). Определим амплитуду выходного напряжения при активном выходном сопротивлении
Как видно, для увеличения напряжения на нагрузке необходимо уменьшать выходное сопротивление четырехполюсника. Найдем переданную в нагрузку мощность
Максимум мощности имеет место при условии
(получите этот результат самостоятельно). Рассмотрим цепь, показанную на рис. 4.7а. Ее можно преобразовать к виду рис. 4.2б, если рассматривать четырехполюсник без нагрузки как реальный источник напряжения с эквивалентной ЭДС
Рис. 4.7
Выходное сопротивление четырехполюсника в цепи на рис. 4.7в равно
Для активной и реактивной составляющих получим следующие соотношения
Рассмотрите самостоятельно составляющие выходного сопротивления, полагая В схеме рис. 4..2б найдем напряжение на нагрузке
Подставляя (4.9) и (4.10), получим
а для амплитуды напряжения соответственно
Зависимость амплитуды напряжения на нагрузке
Рис. 4.8
Определим потребляемую нагрузкой мощность
Зависимость
Рис. 4.9 Проанализируйте самостоятельно полученные зависимости, сделайте выводы. Как видно, расчет входного и выходного сопротивлений четырехполюсника позволяет анализировать возможности подключения к немы различных источников сигнала и нагрузок. Аналогичные исследования можно проводить самостоятельно в лабораторных и курсовых работах.
4.2. Частотные характеристики цепей первого порядка
Под частотными характеристиками четырехполюсника обычно понимают комплексный коэффициент передачи по напряжению
амплитудно-частотную (АЧХ)
и фазо-частотную (ФЧХ)
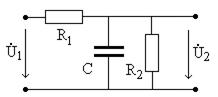
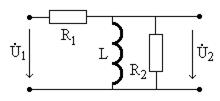
характеристики. Примеры расчета АЧХ и ФЧХ простейших четырехполюсников приведены в [2]. Рассмотрим цепь, показанную на рис. 4.10 при Расчет комплексного коэффициента передачи проводится, полагая известным входное напряжение
Рис. 4.10
В цепи на рис. 4.10 с помощью закона Ома получим
Коэффициент передачи равен
Амплитудно-частотная характеристика цепи имеет вид
а для фазо-частотной характеристики получим
Максимум АЧХ имеет место при
Графики АЧХ и ФЧХ показаны на рис. 4.11.
Рис. 4.11
Граничные частоты
(обратите внимание, что максимум коэффициента передачи
Возводя в квадрат обе части (4.26) и переворачивая дроби, получим
тогда
и далее
В результате верхняя граничная частота полосы пропускания равна
а для полосы пропускания получим
Определим коэффициент прямоугольности. Для этого найдем полосу пропускания
из которого аналогично предыдущему получим
тогда
Коэффициент прямоугольности равен
Проведем расчет частотных характеристик фильтра верхних частот, схема которого показана на рис. 4.12, при .
Рис. 4.12
Подобно (4.20) в цепи на рис. 4.12 с помощью закона Ома получим выражение для выходного напряжения
тогда комплексный коэффициент передачи равен
Для АЧХ и ФЧХ соответственно получим
Графики АЧХ и ФЧХ приведены на рис. 4.13.
Рис. 4.13
Максимум коэффициента передачи
что совпадает с (4.24) Как видно, цепь на рис. 4.12 является фильтром верхних частот. В частотной области его свойства характеризуются полосой удержания
Возведя обе части (4.36) в квадрат и перевернув дроби, получим
в результате для полосы удержания
Определим коэффициент прямоугольности фильтра верхних частот
где
и аналогично (4.37) равна
Тогда из (4.39) коэффициент прямоугольности равен
Определим АЧХ и ФЧХ цепи, показанной на рис. 4.14.
Рис. 4.14
Расчет выходного напряжения
ток
Определим узловое напряжение
и найдем выходное напряжение
В результате комплексный коэффициент передачи четырехполюсника равен
Для АЧХ и ФЧХ получим
Графики частотных характеристик при
Рис. 4.15
4.3. Параметры четырехполюсника
Условно-графическое обозначение четырехполюсника показано на рис. 4.16.
Рис. 4.16
Выбирая в качестве независимых переменных входное
Выбрав независимыми переменными входной ток
В дальнейшем будем рассматривать H-параметры четырехполюсника. Систему Y-параметров рассмотрите аналогично самостоятельно. Параметр
Параметр
Параметр
Параметр
Рассмотрим четырехполюсник, схема которого показана на рис. 4.17 и определим его H-параметры.
Рис. 4.17
Входное сопротивление
Рис. 4.18
В этой же цепи на рис. 4.18а находим коэффициент передачи тока
Для расчета двух остальных параметров необходимо обеспечить режим холостого хода входной цепи, то есть условие Параметр
Выходная проводимость
В результате получим систему уравнений для H-параметров (4.50) в виде
Как видно, первое уравнение представляет собой уравнение первого закона Кирхгофа для цепи на рис 4.17, а второе уравнение – второго закона Кирхгофа. Эта особенность проявляется только для очень простых четырехполюсников. Рассмотрим четырехполюсник, схема которого показана на рис. 4.19.
Рис. 4.19
На рис. 4.20а представлена его схема при замкнутом выходе, а на рис. 4.20б – эквивалентно упрощенная схема с учетом того, что ток через сопротивление
Рис. 4.20
Найдем входное сопротивление
В цепи на рис. 4.20б определим коэффициент передачи тока
а ток через индуктивность соответственно
Так как по схеме рис. 4.20б
Расчет параметра
тогда получим
Рис. 4.21
Выходная проводимость
В результате из (4.50) получим систему уравнений четырехполюсника, в которой в явном виде не просматриваются уравнения Кирхгофа,
Эти уравнения можно получить по методу наложения в схеме цепи, показанной на рис. 4.22, выбрав в качестве искомых величин напряжение
Рис. 4.22
4.4. Колебательные контуры
4.4.1. Методика расчета
Колебательные контуры – это цепи не ниже второго порядка с индуктивностью и емкостью, на которые воздействуют высокочастотные узкополосные сигналы, поэтому их свойства в основном рассматриваются в окрестности резонансной частоты. Расчет цепей с колебательными контурами при воздействии гармонических сигналов проводится методом комплексных амплитуд. В его рамках можно использовать все рассмотренные ранее (в третьем разделе) методы расчета. Если анализ контура ведется в малой окрестности резонансной частоты, то для расчета целесообразно использовать координаты обобщенной расстройки
где
характеристическое сопротивление контура,
4.4.2. Последовательный колебательный контур
Эквивалентная схема последовательного колебательного контура показана на рис. 4.23.
Рис. 4.23
Входное сопротивление
При значениях частоты Например, при
В координатах обобщенной расстройки (4.65) входное сопротивление контура равно
В рассмотренном примере резонансная частота
добротность контура
тогда обобщенная расстройка контура равна
В результате входное сопротивление контура равно
Определим напряжение
Найдем ток в цепи
тогда для комплексной амплитуды напряжения на индуктивности получим
Подставим исходные данные
Очевидно, что выражения и расчеты для
Комплексный коэффициент передачи последовательного колебательного контура равен
его амплитудно-частотная характеристика (АЧХ)
и фазо-частотная характеристика (ФЧХ)
Для предыдущего примера из (4.70) получим
что совпадает с предыдущим значением. Воспользовавшись АЧХ (4.72) и ФЧХ (4.74), аналогично получим
Если известны первичные параметры контура
Рассмотрим задачу определения параметров колебательного контура. Для ее решения необходимо запомнить основные формулы (4.65) – (4.75). Пусть известны
а из (4.68)
Если известны
На свойства последовательного колебательного контура существенное влияние оказывает сопротивление нагрузки, которое чаще всего подключается к емкости, как показано на рис. 4.24а.
Рис. 4.24
Параллельное соединение емкости контура и нагрузки в окрестности резонансной частоты можно пересчитать в последовательное, тогда получим эквивалентную цепь, показанную на рис. 4.24б, совпадающую со схемой контура без нагрузки на рис. 4.23, где
Таким образом, сопротивление нагрузки увеличивает потери в контуре и снижает его эквивалентную добротность, которая с учетом нагрузки определяется выражением
Например, если к контуру с то его эквивалентная добротность будет равна
Рассмотрим четырехполюсник, содержащий последовательный колебательный контур, схема которого показана на рис. 4.25, при
Рис. 4.25
Резонансная частота контура равна
Если проводить расчет в координатах частоты
Тогда модуль
На рис. 4.26 представлена программа расчета и графики АЧХ и ФЧХ в соответствии с (4.78). Проведите аналогичный расчет по выражениям (4.79) и (4.80).
Рис. 4.26
Как видно, выражения для АЧХ и ФЧХ достаточно громоздки. Определим АЧХ и ФЧХ цепи на рис. 4.25 в координатах обобщенной расстройки последовательного колебательного контура равно (4.69) и с помощью закона Ома получим комплексный коэффициент передачи
Для АЧХ и ФЧХ соответственно можно записать
Полученные выражения существенно проще (4.79) и (4.80), программа для расчета частотных характеристик и построения их графиков показана на рис. 4.27.
Рис. 4.27
Формула для перехода от координат обобщенной расстройки
Соответствующий расчет проведен в программе на рис. 4.26 и представлен широким пунктиром на графиках частотных характеристик. Как видно, обеспечивается высокая точность расчета в широком диапазоне значений
Из (4.82) видно, что максимум АЧХ имеет место при
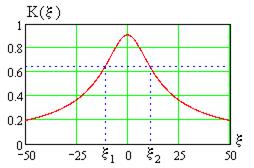
Из формулы (4.79) этот результат не столь очевиден (определите максимум самостоятельно). Определим полосу пропускания полосового частотного фильтра (рис. 4.25) в координатах
и найдем его корни – значения
Интервал
Рис. 4.28
Для полосы пропускания
откуда
Подставляя исходные данные, получим
Аналогично определяется коэффициент прямоугольности рассматриваемого фильтра (проведите расчет самостоятельно).
4.4.3. Параллельный колебательный контур
Эквивалентная схема параллельного колебательного контура показана на рис. 4.29а, а ее эквивалентные варианты – на рис. 4.29б и 4.29в соответственно. На рис. 4.29а тивления потерь в индуктивности и емкости (обычно
и эти величины достаточно малы (доли Ома – десятки Ом).
|

 ,
,  и выходными
и выходными  ,
,  сопротивлениями и проводимостями [2].
сопротивлениями и проводимостями [2].
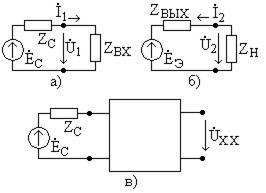
 - ЭДС источника сигнала,
- ЭДС источника сигнала,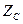 - его внутреннее сопротивление,
- его внутреннее сопротивление,  - ЭДС эквивалентного источника напряжения (по теореме об эквивалентном источнике), равная напряжению холостого хода четырехполюсника со стороны выходных полюсов (рис. 4.2в),
- ЭДС эквивалентного источника напряжения (по теореме об эквивалентном источнике), равная напряжению холостого хода четырехполюсника со стороны выходных полюсов (рис. 4.2в), 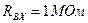 и емкости
и емкости  .
.
 (4.1)
(4.1) и реактивную
и реактивную 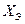 составляющие
составляющие (4.2)
(4.2) (4.3)
(4.3)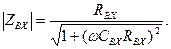 (4.4)
(4.4)
 (1,6 кГц). Реактивная составляющая отрицательна, то есть цепь имеет емкостный характер.
(1,6 кГц). Реактивная составляющая отрицательна, то есть цепь имеет емкостный характер.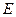 , то фактически на прибор воздействует амплитуда напряжения
, то фактически на прибор воздействует амплитуда напряжения 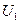 . Комплексная амплитуда
. Комплексная амплитуда 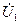 равна
равна
 (4.5)
(4.5) при различных сопротивлениях источника сигнала показана на рис. 4.5. Как видно, точность измерения напряжения источника уменьшается с ростом его внутреннего сопротивления
при различных сопротивлениях источника сигнала показана на рис. 4.5. Как видно, точность измерения напряжения источника уменьшается с ростом его внутреннего сопротивления  и частоты сигнала. Задача точного измерения уровня сигнала источника может быть решена только если
и частоты сигнала. Задача точного измерения уровня сигнала источника может быть решена только если  и
и 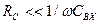 . Для оценки погрешностей необходимо анализировать входное сопротивление (проводимость) измерителя.
. Для оценки погрешностей необходимо анализировать входное сопротивление (проводимость) измерителя.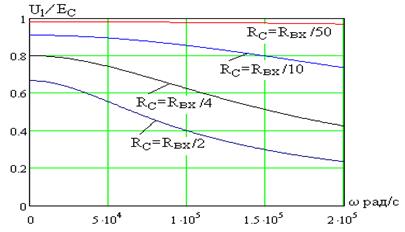



 ,
,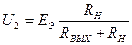 . (4.6)
. (4.6) (4.7)
(4.7)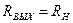 (4.8)
(4.8)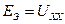 , определяемой в цепи, схема которой показана на рис. 4.7б. Эквивалентная ЭДС определяется по закону Ома
, определяемой в цепи, схема которой показана на рис. 4.7б. Эквивалентная ЭДС определяется по закону Ома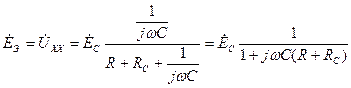 . (4.9)
. (4.9)
 (4.10)
(4.10) (4.11)
(4.11) (4.12)
(4.12) ,
,  для различных
для различных  в диапазоне частот от 0 до
в диапазоне частот от 0 до  .
. . (4.13)
. (4.13) (4.14)
(4.14)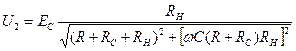 (4.15)
(4.15) от частоты при указанных выше параметрах показана на рис. 4.8.
от частоты при указанных выше параметрах показана на рис. 4.8.
 . (4.16)
. (4.16) от частоты для различных значений нагрузки показана на рис. 4.9а. На рис. 4.9б показана зависимость
от частоты для различных значений нагрузки показана на рис. 4.9а. На рис. 4.9б показана зависимость 
 , (4.17)
, (4.17)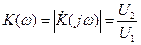 , (4.18)
, (4.18)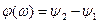 (4.19)
(4.19)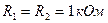 и
и 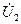 .
.
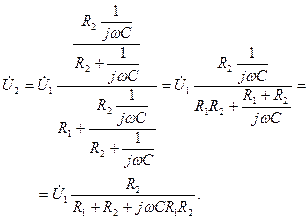 (4.20)
(4.20)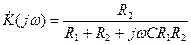 . (4.21)
. (4.21)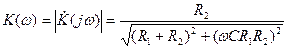 , (4.22)
, (4.22)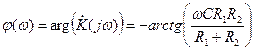 . (4.23)
. (4.23) (докажите это самостоятельно) и равен
(докажите это самостоятельно) и равен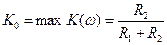 . (4.24)
. (4.24)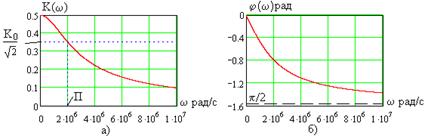
 и
и 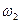 полосы пропускания определяются из уравнения
полосы пропускания определяются из уравнения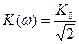 (4.25)
(4.25)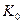 не всегда равен 1). Для фильтра нижних частот на рис. 4.10 нижняя граница полосы пропускания (рис. 4.11а)
не всегда равен 1). Для фильтра нижних частот на рис. 4.10 нижняя граница полосы пропускания (рис. 4.11а)  , а из (4.25) и (4.22), (4.24) находим
, а из (4.25) и (4.22), (4.24) находим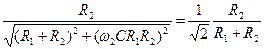 , (4.26)
, (4.26)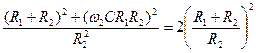 ,
,
 .
. ,
, . (4.27)
. (4.27)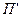 на уровне
на уровне  от максимального коэффициента передачи
от максимального коэффициента передачи 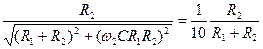 , (4.28)
, (4.28)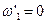 и
и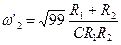 ,
, . (4.29)
. (4.29) . (4.30)
. (4.30) .
.
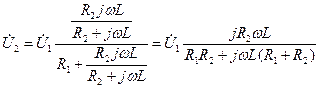 , (4.31)
, (4.31)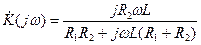 . (4.32)
. (4.32)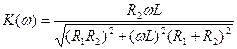 , (4.33)
, (4.33)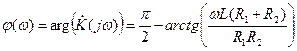 . (4.34)
. (4.34)
 . (4.35)
. (4.35) (рис. 4.13а). Ее нижняя граница
(рис. 4.13а). Ее нижняя граница  . (4.36)
. (4.36)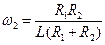 , (4.37)
, (4.37) . (4.38)
. (4.38) , (4.39)
, (4.39) (4.40)
(4.40)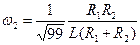 , (4.41)
, (4.41)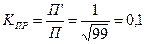 . (4.42)
. (4.42)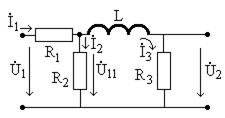
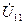 и выразим через него токи всех ветвей
и выразим через него токи всех ветвей
 протекает через элементы
протекает через элементы  и
и 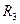 , и не ответвляется в выходную цепь, так как нагрузка четырехполюсника отсутствует (имеет бесконечное сопротивление).Тогда по первому закону Кирхгофа
, и не ответвляется в выходную цепь, так как нагрузка четырехполюсника отсутствует (имеет бесконечное сопротивление).Тогда по первому закону Кирхгофа  получим уравнение метода узловых напряжений
получим уравнение метода узловых напряжений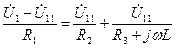 . (4.43)
. (4.43)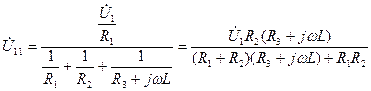 (4.44)
(4.44) . (4.45)
. (4.45)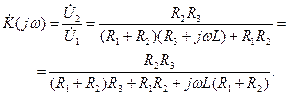 (4.46)
(4.46)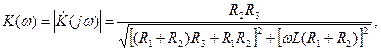 (4.47)
(4.47) (4.48)
(4.48) и
и  показаны на рис. 4.15. Расчет полосы пропускания и коэффициента прямоугольности проведите самостоятельно.
показаны на рис. 4.15. Расчет полосы пропускания и коэффициента прямоугольности проведите самостоятельно.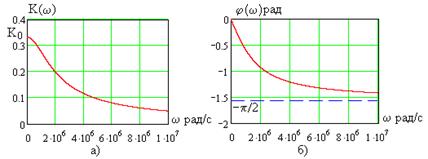

 напряжения, получим систему Y-параметров четырехполюсника
напряжения, получим систему Y-параметров четырехполюсника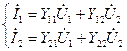 (4.49)
(4.49) и выходное напряжение
и выходное напряжение 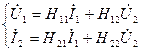 (4.50)
(4.50)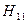 , равный отношению входного напряжения к входному току, является комплексным входным сопротивлением четырехполюсника при коротком замыкании выхода и измеряется в Омах,
, равный отношению входного напряжения к входному току, является комплексным входным сопротивлением четырехполюсника при коротком замыкании выхода и измеряется в Омах,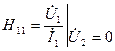 . (4.51)
. (4.51) равен отношению комплексных амплитуд выходного тока к входному и представляет собой безразмерный комплексный коэффициент передачи тока при коротком замыкании выхода,
равен отношению комплексных амплитуд выходного тока к входному и представляет собой безразмерный комплексный коэффициент передачи тока при коротком замыкании выхода, . (4.52)
. (4.52)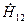 равен отношению комплексных амплитуд входного и выходного напряжений. Его целесообразно назвать комплексным коэффициентом обратной передачи напряжения при холостом ходе входной цепи,
равен отношению комплексных амплитуд входного и выходного напряжений. Его целесообразно назвать комплексным коэффициентом обратной передачи напряжения при холостом ходе входной цепи, . (4.53)
. (4.53) , равный отношению выходного тока к выходному напряжению, является комплексной выходной проводимостью четырехполюсника при холостом ходе входной цепи,
, равный отношению выходного тока к выходному напряжению, является комплексной выходной проводимостью четырехполюсника при холостом ходе входной цепи, , (4.54)
, (4.54)
 . (4.55)
. (4.55)
 ток как токи в элементах
ток как токи в элементах  и
и 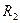 равны нулю (они замкнуты перемычкой и напряжение на них равно нулю). тогда
равны нулю (они замкнуты перемычкой и напряжение на них равно нулю). тогда . (4.56)
. (4.56) (схема цепи показана на рис. 4.18б).
(схема цепи показана на рис. 4.18б). , тогда при
, тогда при  и
и . (4.57)
. (4.57)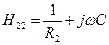 . (4.58)
. (4.58)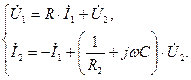 (4.59)
(4.59)
 . (4.60)
. (4.60) на параллельно соединенных элементах
на параллельно соединенных элементах  ,
,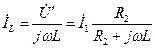 .
.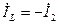 , то коэффициент передачи тока четырехполюсника равен
, то коэффициент передачи тока четырехполюсника равен . (4.61)
. (4.61) , показана на рис. 4.21б. Положим известным выходное напряжение
, показана на рис. 4.21б. Положим известным выходное напряжение  ,
, . (4.62)
. (4.62)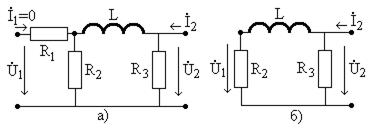
 для цепи на рис. 4.21б равна проводимости параллельного соединения сопротивления
для цепи на рис. 4.21б равна проводимости параллельного соединения сопротивления  . (4.63)
. (4.63)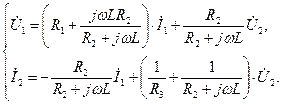 (4.64)
(4.64) (проведите расчет самостоятельно).
(проведите расчет самостоятельно).
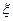 , равной
, равной , (4.65)
, (4.65) - добротность контура,
- добротность контура, , (4.66)
, (4.66) (4.67)
(4.67)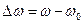 или
или  - абсолютная расстройка контура,
- абсолютная расстройка контура,  - резонансная частота,
- резонансная частота,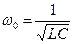 ,
, 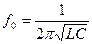 . (4.68)
. (4.68)
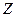 последовательного колебательного контура относительно точек подключения источника напряжения в координатах абсолютной частоты равно
последовательного колебательного контура относительно точек подключения источника напряжения в координатах абсолютной частоты равно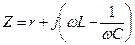 .
.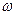 , близких к резонансной частоте контура
, близких к резонансной частоте контура  (4.68), реактивные сопротивления индуктивности
(4.68), реактивные сопротивления индуктивности 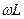 и емкости
и емкости 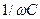 велики и близки между собой, а их разность сравнительно мала, что даже в этом случае затрудняет точные вычисления.
велики и близки между собой, а их разность сравнительно мала, что даже в этом случае затрудняет точные вычисления.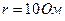 ,
, 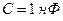 на частоте
на частоте 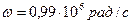 получим
получим
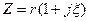 . (4.69)
. (4.69) ,
,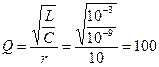 ,
,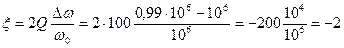 .
. .
. на индуктивности контура (рис. 4.23) при
на индуктивности контура (рис. 4.23) при  . Комплексная амплитуда ЭДС равна
. Комплексная амплитуда ЭДС равна  и частота гармонического сигнала
и частота гармонического сигнала 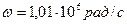 . Добротность контура определена ранее и равна
. Добротность контура определена ранее и равна 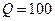 , а обобщенная расстройка имеет вид
, а обобщенная расстройка имеет вид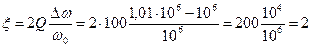 .
.
 .
.
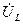 в координатах частоты
в координатах частоты 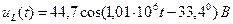 .
.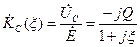 , (4.70)
, (4.70) , (4.71)
, (4.71)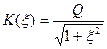 (4.72)
(4.72) , (4.73)
, (4.73)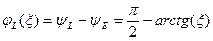 , (4.74)
, (4.74)

 , то по ним можно определить вторичные параметры
, то по ним можно определить вторичные параметры 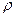 , полосу пропускания
, полосу пропускания  ,
, или
или 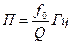 . (4.75)
. (4.75) ,
,  и необходимо определить сопротивление потерь
и необходимо определить сопротивление потерь 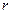 . Из (4.66)
. Из (4.66)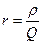 ,
,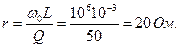
 ,
,  .
.
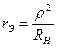 . (4.76)
. (4.76) . (4.77)
. (4.77) ,
, .
. , и определим его частотные характеристики в окрестности резонансной частоты контура.
, и определим его частотные характеристики в окрестности резонансной частоты контура.
 .
. (4.78)
(4.78)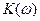 (АЧХ) и аргумент
(АЧХ) и аргумент  (ФЧХ) коэффициента передачи соответственно равны
(ФЧХ) коэффициента передачи соответственно равны (4.79)
(4.79)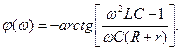 (4.80)
(4.80)
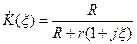 . (4.81)
. (4.81) . (4.82)
. (4.82)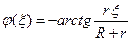 . (4.83)
. (4.83)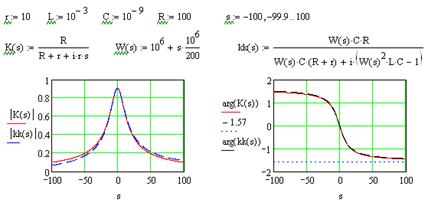
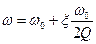 . (4.84)
. (4.84) . (4.85)
. (4.85) (минимум знаменателя) и равен
(минимум знаменателя) и равен . (4.86)
. (4.86)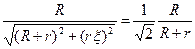 (4.87)
(4.87) и
и  на границе полосы пропускания. Перевернув дроби и возведя обе части уравнения в квадрат, получим
на границе полосы пропускания. Перевернув дроби и возведя обе части уравнения в квадрат, получим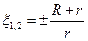 . (4.88)
. (4.88) обобщенных расстроек внутри полосы пропускания равен
обобщенных расстроек внутри полосы пропускания равен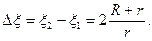
 ,
,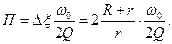 (4.89)
(4.89)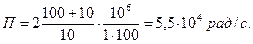
 и
и 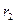 - сопро-
- сопро-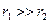 ),
), , (4.90)
, (4.90)


