КОМПЛЕКСНЫХ АМПЛИТУД
3.1. Расчет цепи на основе закона Ома
С помощью только закона Ома удобно проводить расчет гармонических токов и напряжений в простой цепи с одним источником сигнала. В исходной цепи задаются положительные направления и условные обозначения токов и напряжений элементов, определяются комплексные амплитуды источников и комплексные сопротивления элементов. Вычисляется комплексное сопротивление (проводимость) цепи относительно зажимов источника. Затем определяется общий ток (напряжение) в цепи и далее вычисляются искомые токи и напряжения. В качестве примера рассмотрим цепь, показанную на рис. 3.1а, при
Рис. 3.1
Определим комплексную амплитуду ЭДС источника
частота сигнала равна Вычислим комплексное сопротивление цепи относительно точек подключения источника,
Тогда общий ток цепи
и напряжение
Определим напряжение
и токи в элементах
Расчет сопротивлений, токов и напряжений проведен в программе, показанной на рис. 3.2 (повторите вычисления самостоятельно с помощью калькулятора и программы).
Рис. 3.2
Результаты расчета приведены в таблице.
Рассмотрим цепь, показанную на рис. 3.3а, при
Введем условные обозначения и положительные направления токов и напряжений в элементах цепи, обозначим их комплексные амплитуды (рис. 3.3б).
Рис. 3.3
Комплексная амплитуда тока источника равна
Определим проводимость цепи относительно точек подключения источника
тогда комплексное сопротивление этой цепи будет равно
Комплексная амплитуда общего напряжения цепи
а для токов ветвей соответственно
Нетрудно убедиться, что выполняется первый закон Кирхгофа
Убедитесь, что аналитически и численно выполняется второй закон Кирхгофа На рис. 3.4 приведена программа расчета комплексных амплитуд токов и напряжений. Там же определены их амплитуды и начальные фазы (приведите вычисления и преобразования комплексных чисел в различные формы самостоятельно).
Рис. 3.4
3.2. Общий метод расчета цепи по уравнениям Кирхгофа
В цепи задаются положительные направления и условные обозначения всех токов и напряжений ветвей (элементов) [1]. Определяются числа узлов Составляется подсистема компонентных уравнений цепи для каждого элемента (ветви) на основе закона Ома. Записывается подсистема топологических уравнений цепи на основе законов Кирхгофа. По первому закону составляются
Из компонентных уравнений выражаются токи ветвей и подставляются в топологические уравнения. Получается система уравнений для комплексных амплитуд напряжений ветвей. Аналогично из компонентных уравнений выражаются напряжения ветвей и подставляются в топологические уравнения. В результате формируется система уравнений для комплексных амплитуд токов ветвей. Проведем расчет токов и напряжений в цепи, показанной на рис. 3.5а (ранее она рассматривалась на рис. 3.1), при
Рис. 3.5
Запишем подсистему компонентных уравнений
В цепи
Число ветвей
Выражая из (3.1) напряжения через токи (это уже сделано) и подставляя их в (3.3), получим систему уравнений для токов ветвей
Для ее решения выразим из последнего уравнения ток
и подставим его в остальные уравнения (3.4), получим
Из первого уравнения найдем ток
и ток емкости равен
Из первого уравнения (3.6) с учетом (3.7) получим
а из (3.5)
(приведите вычисления и преобразования комплексных чисел в различные формы самостоятельно). Как видно, результаты расчета токов ветвей (3.7)-(3.9) совпадают с полученными ранее для цепи на рис. 3.1. Зная токи ветвей, вычислим напряжения на элементах цепи по уравнениям закона Ома (3.1) (проведите расчет самостоятельно). Проведем расчет токов и напряжений в цепи, показанной на рис. 3.6 при
Вычислим комплексные амплитуды ЭДС источника напряжения сигналов
На основе закона Ома запишем компонентные уравнения
В цепи
Число ветвей без идеального источника тока
Полная система уравнений включает в себя (3.10) - (3.12). Выражая из (3.10) токи ветвей через напряжения, получим систему уравнений для напряжений ветвей
Из второго уравнения найдем напряжение
и подставив его в первое уравнение, получим
Решая уравне6ние (3.15), найдем напряжение
Из (3.14) найдем напряжение на индуктивности
По закону Ома найдем токи ветвей
На рис. 3.7 приведена программа расчета токов и напряжений.
Рис. 3.7
Проведем расчет токов и напряжений в цепи, показанной на рис. 3.8 при
Рис. 3.8
В цепи
По первому закону Кирхгофа запишем одно уравнение
а по второму закону – два уравнения (
(внимательно разберитесь со знаками). Подставляя (3.18) в (3.20) с учетом (3.19) получим систему уравнений для токов ветвей в виде
Из второго уравнения выразим
и подставим его в (3.21), получим
Из второго уравнения (3.23) найдем
и подставим его в первое, тогда
В результате найдем ток емкости (учтем, что
Подставляя (3.25) в (3.24), определим ток индуктивности
а из (3.22) определим ток через сопротивление
На рис. 3.9 приведена программа вычисления токов ветвей. Там же показана программа численного решения системы уравнений (3.21).
Рис. 3.9
Проведите вычисления самостоятельно, определите напряжения на элементах цепи, амплитуды и начальные фазы токов и напряжений. Систему уравнений (3.21) можно записать в каноническом виде
и решить ее с помощью метода Крамера (приложение 1). Определитель (детерминант) системы равен
Токи ветвей определяются выражениями
где
Программа расчета показана на рис. 3.10 (команда вычисления определителя находится в меню «Матрицы»).
Рис. 3.10
Для токов ветвей получим следующие выражения (сравните их (3.25)-(3.27))
Проведите вычисления самостоятельно, сравните с предыдущими результатами. 3.4. Метод контурных токов
Метод контурных токов базируется на уравнениях второго закона Кирхгофа [1]. В цепи выбираются Рассмотрим простую цепь, показанную на рис. 3.11 при
Рис. 3.11
Выразим токи ветвей через контурные токи (через емкость протекает ток
Контурный ток
По закону Ома выразим через контурные токи напряжения ветвей
Для второго контура запишем уравнение второго закона Кирхгофа
Подставляя (3.30), получим
а с учетом (3.29) можно записать
откуда найдем контурный ток
С помощью (3/28) найдем токи ветвей
Напряжение на элементах
Проведите вычисления самостоятельно, определите амплитуды и начальные фазы токов и напряжений. Определим токи и напряжения в цепи, показанной на рис. 3.12 при
Рис. 3.12 Через индуктивность протекает ток
Выразим через контурные токи напряжения ветвей
В цепи на рис. 3.11 запишем уравнения второго закона Кирхгофа (
Подставляя (3.37) в (3.38), получим
Из второго уравнения (3.39) выразим
и подставим его в первое уравнение (3.39), тогда
а после преобразования получим
Из (3.40) найдем ток
Подставляя (3.42) в (3.36), получим токи ветвей
Программа расчета токов ветвей приведена на рис. 3.13.
Рис. 3.13
Проведите вычисления самостоятельно, желательно с помощью калькулятора и программы, определите напряжения на элементах цепи, амплитуды и начальные фазы токов и напряжений.
Проведем расчет токов и напряжений в цепи, показанной на рис. 3.14 (ранее она рассмотрена на рис. 3.6) при
Рис. 3.14
Комплексные амплитуды источников равны
и найдем напряжения ветвей
В цепи
Для контура с током
Из (3.44) – (3.46) можно записать
тогда
Токи ветвей равны
Выполняется первый закон Кирхгофа Для напряжений ветвей получим
Выполняется уравнение второго закона Кирхгофа (3.45). Определим напряжение на индуктивности
Мгновенные значения напряжения описываются выражением
3.5. Метод узловых напряжений
Метод узловых напряжений базируется на первом законе Кирхгофа и требует составления Рассмотрим цепь, показанную на рис. 3.15 при В цепи два узла, нижний узел объявляется базисным, вводится узловое напряжение
Рис. 3.15
Запишем уравнение первого закона Кирхгофа
тогда с учетом (3.51) получим уравнение метода узловых напряжений
Из (3.52) найдем узловое напряжение
Тогда токи ветвей равны
Численные расчеты уже проведены для цепи на рис. 3.10 (повторите их самостоятельно и сравните результаты). Определим ток в сопротивлении
Рис. 3.16
Выразим токи ветвей через узловое напряжение. Для ветви с индуктивностью запишем уравнение второго закона Кирхгофа
С учетом закона Ома
получим
тогда
Токи в сопротивлении и емкости равны
По первому закону Кирхгофа запишем одно уравнение (в цепи два узла)
Подставляя в (3.59) токи из (3.56) – (3.58), получим уравнение метода узловых напряжений (потенциалов)
Найдем узловое напряжение
тогда для напряжений ветвей получим
а искомый ток через сопротивление равен
Подставляя исходные данные, получим
тогда мгновенные значения тока определяются выражением
Проведем расчет напряжения на индуктивности
Рис. 3.17
По второму закону Кирхгофа и закону Ома получим
тогда ток
Ток индуктивности найдем по закону Ома
По первому закону Кирхгофа запишем одно уравнение
Подставляя в него (3.65) и (3.66), получим уравнение метода узловых напряжений
Решая уравнение, получим
Напряжение на индуктивности равно
Подставляя исходные данные, получим
тогда мгновенные значения имеют вид
Рассчитаем напряжение
Рис. 3.18
Выразим токи ветвей через узловые напряжения. Для контура с элементами
тогда с учетов
получим
Для контура с элементами
и по закону Ома
тогда ток
Токи в сопротивлении ются по закону Ома
По первому закону Кирхгофа записываем
Подставляя в (3.74) выражения (3.70) – (3.73), получим по методу узловых напряжений систему из двух уравнений
Преобразуя, получим
Из второго уравнения (3.76) выразим
и подставим его в первое, тогда
Преобразуя, для узлового напряжения
Узловое напряжение
а после алгебраических преобразований получим
Комплексная амплитуда напряжения
На рис. 3.19 приведена программа расчета
Рис. 3.19
Проведите вычисления самостоятельно с помощью калькулятора и программы. В результате получим
3.6. Метод наложения
По методу наложения реакция цепи (ток или напряжение) на воздействие нескольких источников равна сумме тех же реакций на действие каждого из источников в отдельности, при этом остальные источники должны быть выключены (идеальные источники напряжения заменены коротким замыканием, а источники тока – разрывом цепи) [1]. Проведем расчет напряжения на индуктивности
Рис. 3.20 Выключим источник тока (заменим его холостым ходом – разрывом цепи), получим схему на рис. 3.21а.
Рис. 3.21
Искомое напряжение
Выключим источник напряжение (заменим его коротким замыканием), схема показана на рис. 3.21б. В ней по закону Ома найдем
Результирующее напряжение на индуктивности по методу наложения равно
Подставляя исходные данные, получим
и мгновенные значения напряжения имеют вид
Определим ток индуктивности
Рис. 3.22
Выключим источник напряжения
Рис. 3.23
Из уравнения первого закона Кирхгофа
Дата добавления: 2015-09-04; просмотров: 1237. Нарушение авторских прав; Мы поможем в написании вашей работы! Постинъекционные осложнения, оказать необходимую помощь пациенту I.ОСЛОЖНЕНИЕ: Инфильтрат (уплотнение). II.ПРИЗНАКИ ОСЛОЖНЕНИЯ: Уплотнение...
Словарная работа в детском саду Словарная работа в детском саду — это планомерное расширение активного словаря детей за счет незнакомых или трудных слов, которое идет одновременно с ознакомлением с окружающей действительностью, воспитанием правильного отношения к окружающему...
|
, 
и 
. Зададим условные обозначения и положительные направления токов и напряжений элементов цепи, обозначим их комплексные амплитуды (рис. 3.1б).
,
.
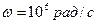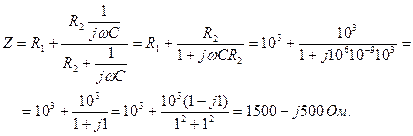
(ток источника) равен
на сопротивлении 
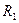определяется выражением
на параллельном соединении элементов
и 
, 
, 
и 
.
. Напряжения на последовательно соединенных элементах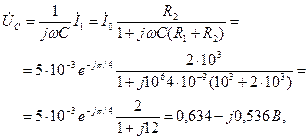 
.
и ветвей 
, не содержащих идеальные источники тока. Выбираются 
независимых контуров и задаются направления их обхода (обычно по часовой стрелке). Определяются комплексные амплитуды ЭДС и токов источников.
уравнений для токов ветвей, а по второму закону
(3.1)
узла, поэтому по первому закону Кирхгофа составляется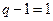 
уравнение вида
(3.2)
, тогда по второму закону Кирхгофа составляется 
уравнения вида
(3.3)
(3.4)
(3.5)
(3.6)
и подставим во второе, тогда
(3.7)
(3.8)
(3.9)
, 
, 
. Зададим условные обозначения и положительные направления токов и напряжений элементов цепи, обозначим их комплексные амплитуды.
Запишем гармонические сигналы источников в канонической форме
,
.
и тока источника тока 
, частота Рис. 3.6
(3.10)
(3.11)
и по второму закону Кирхгофа необходимо составить 
уравнение
(3.12)
(3.13)
(3.14)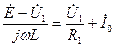
. (3.15)
(3.16)
(3.17)
(3.16)
(3.17)
, 
, 
, 
и 
и тока источника тока 
(проведите преобразования самостоятельно).
(3.18)
, (3.19)
(3.20)
(3.21)
,
, (3.22)
(3.23)
,
, (3.24)
.
)
(3.25)
(3.26)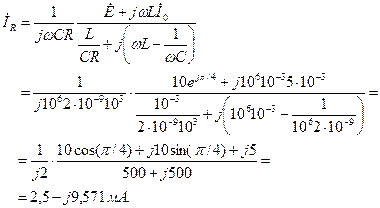
. (3.27)
.
- определители, получающиеся из детерминанта заменой 
-го столбца (
) столбцом из свободных членов системы уравнений,
(
- число ветвей цепи) независимых контуров, в каждом из них задается контурный ток и через контурные токи выражаются токи, а затем и напряжения ветвей, которые подставляются в уравнения второго закона Кирхгофа..
, 
, тогда его комплексная амплитуда равна 
, а частота 
рад/с. Обозначим токи и напряжения ветвей и контурные токи 
и 
.
и встречно ему ток 
(3.28)
,
. (3.29)
(3.30)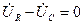
.
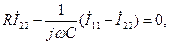(3.31)
(3.32)
(3.33)
(3.34)
равно
(3.35)
, 
, 
. Комплексная амплитуда ЭДС равна 
, а частота 
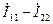, а ток емкости равен 
(3.36)
(3.37)
)
(3.38)
(3.39)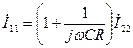
(3.40)
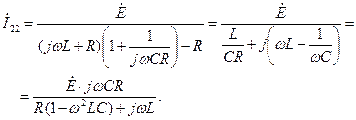(3.41)
. (3.42)
и 
, частота 
(3.43)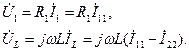
(3.44)
и число ветвей, не содержащих идеальные источники тока, равно 
. Число независимых контуров равно 
, тогда для контура с током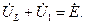 
(3.45)
. (3.46)
, (3.47)
. (3.48)
(3.49)
(проверьте это самостоятельно).
(3.50)
.
. Определим токи ветвей
(3.51)
,
. (3.52)
. (3.53)
, (3.54)
. (3.55)
в цепи, показанной на рис. 3.16 при 
,
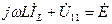. (3.56)
, (3.57)
. (3.58)
. (3.59)
. (3.60)
, (3.61)
, (3.62)
, (3.63)
. (3.64)
.
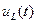в цепи, показанной на рис. 3.17 (ранее она была рассмотрена на рис. 3.6 и рис. 3.14) при 
, 
,
. (3.65)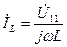
. (3.66)
.
. (3.67)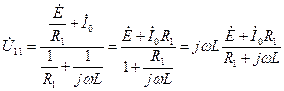
. (3.68)
. (3.69)
.
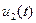на сопротивлении 
, 
. Комплексные амплитуды источников равны 
и 
. Обозначим положительные направления и условные обозначения токов и напряжений, введем два узловых напряжения (в цепи три узла).
запишем уравнение второго закона Кирхгофа
,
. (3.70)
по второму закону Кирхгофа
,
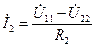. (3.71)
. (3.72)
. (3.73)
уравнения
(3.74)
(3.75)
(3.76)
(3.77)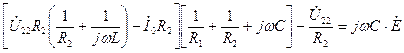
.
получим
. (3.78)
,
. (3.79)
на сопротивлении 
. (3.79)
, 
и выражение для мгновенных значений искомого напряжения
.
, частота 
(реакция цепи) определяется по закону Ома
. (3.80)
. (3.81)
. (3.82)
в цепи на рис. 3.22 при 
, 
, 
, 
, а частота 
, получим цепь на рис. 3.23а. Проведем ее расчет методом узловых напряжений. Выразим через напряжение 
все токи ветвей
(3.82)
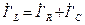с учетом (3.82) получим уравнение
