Динамика
Примеры решения задач 5. Система состоит из частицы 1 массой 1,0 г, расположенной в точке с координатами (1, 1, 1) м, частицы 2 массой 2,0 г, расположенной в точке с координатами (-2, 2, 2) м, частицы 3 массой 3,0 г, расположенной в точке с координатами (-1, 3, -2) м, частицы 4 массой 4,0 г, расположенной в точке с координатами (3, -3, 3) м. Найти радиус – вектор
Модуль радиус-вектора центра масс системы | Ответ: 6. На горизонтальной плоскости лежит доска массой m 1 = 1 кг, а на доске – брусок массой m 2 = 2кг. Коэффициент трения между бруском и доской μ1 = 0,25, между доской и горизонтальной плоскостью μ2 = 0,5. С каким ускорением должна двигаться доска, чтобы брусок начал с нее соскальзывать? Какую горизонтальную силу F 0 следует при этом приложить к доске?
Движения доски и бруска одномерные и происходят вдоль оси OX, как показано на рисунке. Поэтому для решения задачи достаточно воспользоваться проекцией уравнения 2-го закона Ньютона на ось OX (как для бруска, так и для доски). Брусок в горизонтальном направлении вынуждает двигаться с ускорением без проскальзования сила трения покоя со стороны поверхности доски. По мере роста ускорения доски растет и величина силы трения покоя. Когда она достигает предельной величины, равной силе трения скольжения F тр2, брусок начинает соскальзывать с доски. В этом случае из 2-го закона Ньютона получим m 2 Wm = F тр2 = μ1 Fn 2 (1) где Fn 2 – сила нормального давления бруска на поверхность доски. Fn 2 = m 2 g. (2) Из выражений (1) и (2) следует: Wm = μ1∙ g = 0,25∙9,81 = 2,45 м/с². На доску действуют в горизонтальной плоскости силы m 1 Wm = F 0 – F тр1 – F тр2, (3) где F тр1 = μ2 Fn 1 – сила трения скольжения между доской и горизонтальной плоскостью; Fn 1 – сила нормального давления доски с брусом на горизонтальную плоскость. Fn 1 = (m 1+ m 2) g. (4) Из выражений (3) и (4) получим: F 0 = m 1μ1 g + m 2μ1 g +μ2(m 1 + m 2) g = (m 1 + m 2) (μ1 +μ2) g = 22 Н. Ответ: Wm = 2,5 м/с²; F 0 = 22 Н.
|

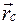 центра масс системы и его модуль.
центра масс системы и его модуль.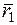 = 1
= 1 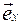 +1
+1 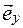 +1
+1 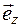 ,м
,м
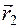 = -2
= -2 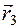 = -1
= -1 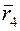 = 3
= 3  где mi – масса i -й частицы системы;
где mi – масса i -й частицы системы;  –?
б) |
–?
б) | 
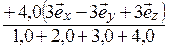 =
=  , м.
, м.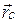 | =
| = 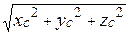 =
=  = 1,27 м.
= 1,27 м.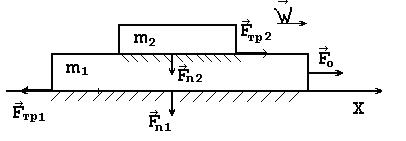
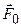 ,
,  и
и 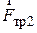 , как показано на рисунке. Уравнение движения доски в этом случае имеет вид:
, как показано на рисунке. Уравнение движения доски в этом случае имеет вид:


