Вращательное движение. Моменты инерции, силы, импульса
Примеры решения задач 7. Сила с компонентами (2, -1, 4), H приложена к точке с координатами (–3, 2, 1), м. Найти: а) момент силы б) модуль момента силы M; в) проекцию Mz момента силы
z – компонента вектора Следовательно, Mz = -1, Н×м. Модуль момента силы получится из выражения вышеприведенного: Ответ: 8. Во сколько раз уменьшится момент инерции однородного сплошного диска оносительно оси, проходящей через его центр инерции (точка О) и перпендикулярной к плоскости диска, если сделать круглый дисковый вырез, как показано на рисунке.
Момент инерции – величина аддитивная. Поэтому момент инерции I3 диска с вырезом относительно точки О равен разности момента инерции диска
где Ответ: момент инерции диска после сделанного выреза уменьшается в 1,2 раза.
9. Тонкий однородный обруч массой m = 2,0 кг и радиусом R = 1,0 м вращается вокруг оси симметрии, перпендикулярной к плоскости обруча, делая n 0 = 120 об/мин. Под действием постоянной касательной к поверхности обруча силы F т = 4,0 Н обруч тормозится и останавливается. Определить время торможения t т и число оборотов N т, которое сделает обруч от начала торможения до остановки.
где ω0 – начальная угловая скорость обруча. Знак «минус» в выражении (2) показывает, что вращение равнозамедленное. Число оборотов N связано с углом поворота обруча φ
В конце времени торможения угловая скорость обруча равна нулю, и из формул (1) и (2) получим
Для числа оборотов N т за время торможения из выражения (3) следует:
Ответ: t т = 6,3 с; N т = 13 об.
10. Небольшое тело массой m = 200 г брошено по углом α= 60° к горизонту со скоростью Определить модуль изменения момента импульса
где Плечо l найдем как l =
Время достижения телом точки наивысшего подъема Время достижения телом точки А в два раза больше времени Окончательно производя необходимые вычисления, получим для Ответ:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1.24. Сфера радиусом R = 2,0 м равномерно вращается вокруг вертикальной оси симметрии, делая 30 об/мин. Внутри сферы находится шарик. Найти высоту h, соответствующую положению равновесия шарика. При какой наименьшей угловой скорости радиус вращения шарика будет 0,9 R? Шарик считать материальной точкой. (h = 1,0 м;ω = 3, 4 рад/с) 1.25. Тело участвует в двух вращательных движениях, происходящих со скоростями а) на какой угол j повернется тело за первые 3,0 с; б) какой угол составляет ось вращения, вокруг которой происходит поворот, с осью Х. (а) j = 20 рад, б) a = 63°) 1.26. Тело вращается вокруг неподвижной оси так, что угол его поворота меняется в зависимости от времени t по закону ( 1.27. Материальная точка движется по окружности радиусом R со скоростью u = kt, где k >0. Найдите зависимость от времени модуля полного ускорения точки; постройте графики зависимости тангенциального и нормального ускорений от времени. ( 1.28. Определить полное ускорение W в момент времени t = 3,0 c точки, находящейся на ободе колеса радиусом R = 0,50 м, вращающегося согласно уравнению j = Аt + Вt 3, где А = 2,0 рад/с; В = 0,20 рад/c3. Изобразите графики нормального и полного ускорений Wn = f (t) и W = f (t) на интервале 0< t <3 с. (W = 27 м/с2) 1.29. Точка движется по окружности с постоянным тангенциальным ускорением. Через некоторый промежуток времени t после начала движения, угол между полным ускорением и радиусом окружности равен 45°. Чему равно угловое ускорение точки? (e 1.30. Материальная точка (частица) массой m брошена под углом a к горизонту с начальной скоростью
Найти зависимость от времени: а) момента силы б) момента импульса частицы (а) 1.31. Две материальные точки массами m 1 и m 2 соединены жестким невесомым стрежнем длиной L. Найти положение центра масс системы Х с и момент инерции I этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс. ( 1.32. Тело массой m = 0,10 кг брошено с некоторой высоты в горизонтальном направлении со скоростью u0 = 20 м/с. Найти модуль приращения момента импульса тела ( 1.33. Сила с компонентами (3, 4, 5) Н приложена к точке с координатами (4, 2, 3) (м). Найти: а) момент силы б) модуль вектора в) проекцию на ось Z момента силы Мz. ( 1.34. Найти момент инерции однородной прямоугольной пластинки массой m, длиной а и шириной b относительно перпендикулярной к ней оси, проходящей через одну из вершин пластинки. ( 1.35. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m 1 = 12 кг. На цилиндр намотан шнур, к которому привязали гирю массой m 2 = 1,0 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири? (W = 1,4 м/с2; T = 8,4 Н) 1.36. На обод маховика диаметром D = 60 c м намотан шнур, к концу которого привязан груз массой m = 2,0 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3,0 с приобрел угловую скорость w = 9,0 рад/с. (J = 1,8 кг×м2) 1.37. Тонкий обруч радиусом R раскрутили вокруг его оси до угловой скорости ( 1.38. С какой угловой скоростью должен вращаться сосуд в виде усеченного конуса, чтобы шарик, лежащий на его дне, выкатился из него? Диаметр верхнего основания равен d. Стенки сосуда наклонены к горизонту под углом a. ( 1.39. Из сплошного однородного цилиндра радиусом R сделали полый, удалив внутреннюю часть радиусом R /2 от оси симметрии. Во сколько раз изменится момент инерции тела относительно указанной оси? ( 1.40. Из сплошного однородного цилиндра сделали полый, удалив половину его массы. Как изменится момент инерции J цилиндра относительно его оси и во сколько раз? Как и во сколько раз изменится момент импульса указанных цилиндров, если они вращаются с одинаковой угловой скоростью? ( 1.41. В сплошном однородном диске радиусом R просверлили сквозное отверстие радиусом R /2 от оси симметрии. Как изменится момент инерции тела относительно указанной оси по отношению к первоначальному? ( 1.42. Два однородных цилиндра с одинаковыми высотами h и равными массами m вращаются относительно своих осей симметрии. Соотношение плотностей материалов цилиндров r1 = (3/4)r2. Сравнить вращающие моменты сил, если угловые ускорения цилиндров одинаковы, а моменты сил трения М тр равны. ( 1.43. Грузик массой 5,0 г, привязанный к нити длиной l = 50 см, вращается вокруг вертикальной оси и описывает окружность в горизонтальной плоскости. Какой угол j образует нить с вертикалью, если частота вращения n = 1,0 c -1. Чему равен модуль проекции момента импульса на ось вращения? (j = 60°; L
|

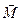 относительно начала системы координат;
относительно начала системы координат; , Н
, Н
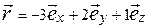 ,м
,м
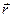 и силы
и силы  .
.
 б)
б)  в)
в) 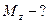

 ] =
] = 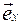
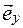
 = (yFz - zFy)
= (yFz - zFy) 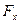
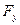
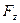 +(xFy – yFx)
+(xFy – yFx)  =
= 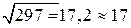 , Н∙м.
, Н∙м. , Н×м; M = 17,2 Н×м; Mz = –1 Н×м.
, Н×м; M = 17,2 Н×м; Mz = –1 Н×м.
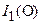 относительно точки О и момента инерции малого диска
относительно точки О и момента инерции малого диска 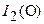 , соответствующего вырезанной части, также относительно точки О, т. е.
, соответствующего вырезанной части, также относительно точки О, т. е. 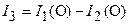 . В задаче необходимо найти отношение
. В задаче необходимо найти отношение 
 . Обозначим массу диска через m, а радиус диска через R. Тогда масса вырезанной части
. Обозначим массу диска через m, а радиус диска через R. Тогда масса вырезанной части 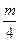 , а радиус
, а радиус 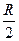 . Как известно, момент инерции диска
. Как известно, момент инерции диска  . Для вычисления момента инерции
. Для вычисления момента инерции  ,
, – момент инерции малого диска, соответствующего вырезанной части, относительно оси симметрии этого диска, походящей через точку О′. Окончательно
– момент инерции малого диска, соответствующего вырезанной части, относительно оси симметрии этого диска, походящей через точку О′. Окончательно  . Таким образом, искомое отношение
. Таким образом, искомое отношение  = 1,23
= 1,23  .
.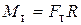 , уравнение вращательного движения имеет вид
, уравнение вращательного движения имеет вид
 (1)
где I – момент инерции обруча, ε – угловое ускорение. Момент инерции тонкого однородного обруча I = mR ². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой
(1)
где I – момент инерции обруча, ε – угловое ускорение. Момент инерции тонкого однородного обруча I = mR ². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой
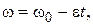 (2)
(2)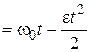 соотношением
соотношением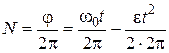 . (3)
. (3) с
с 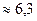 с.
с.
 об.
об.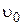 = 10 м/с. Выразить зависимость момента импульса тела
= 10 м/с. Выразить зависимость момента импульса тела  от времени в системе координат, изображенной на рисунке, относительно точки О.
от времени в системе координат, изображенной на рисунке, относительно точки О.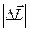 для положения тела в точке наивысшего подъема О΄ и точке падения на землю А.
для положения тела в точке наивысшего подъема О΄ и точке падения на землю А.

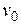 = 10 м/с
= 10 м/с
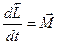 можно определить момент импульса
можно определить момент импульса

 , в котором mg – сила тяжести, l – плечо силы относительно точки О. Знак (-) обусловлен тем, что момент силы
, в котором mg – сила тяжести, l – плечо силы относительно точки О. Знак (-) обусловлен тем, что момент силы 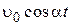 , так как вдоль оси x силы не действуют и движение равномерное. Тогда момент импульса
, так как вдоль оси x силы не действуют и движение равномерное. Тогда момент импульса . (1)
. (1)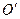 определяется выражением
определяется выражением  с (так как
с (так как  ).
). (как известно, время подъема равно времени спуска тела).
(как известно, время подъема равно времени спуска тела).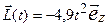 (кг×м2)/с; для модуля изменения момента импульса из (*), учитывая, что в начальный момент времени
(кг×м2)/с; для модуля изменения момента импульса из (*), учитывая, что в начальный момент времени 

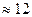 (кг∙м²)/с.
(кг∙м²)/с. (кг∙м²)/с;
(кг∙м²)/с;  (кг∙м²)/с.
(кг∙м²)/с.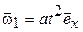 и
и  (a = 1,0 рад/с3). Определить:
(a = 1,0 рад/с3). Определить: , где а >0; b >0. Найти момент времени t, в который тело остановится, а также число оборотов N тела до остановки.
, где а >0; b >0. Найти момент времени t, в который тело остановится, а также число оборотов N тела до остановки.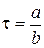 ;
; 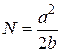 )
)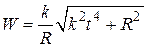 )
)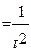 )
) . Траектория полета частицы лежит в плоскости Х, Y. Ось Z направлена "на нас".
. Траектория полета частицы лежит в плоскости Х, Y. Ось Z направлена "на нас".


 , действующего на частицу;
, действующего на частицу;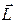 относительно начала координат.
относительно начала координат.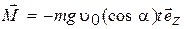 ; б)
; б) 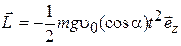 ).
). ;
;  )
) относительно точки бросания за первые t = 5 с.
относительно точки бросания за первые t = 5 с.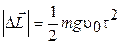 = 2,5 ∙102 кгм2/с)
= 2,5 ∙102 кгм2/с)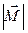 ;
; (Н×м),
(Н×м), 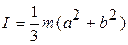 )
) и положили (опустили) на горизонтальный стол. Через какое время t обруч остановится, если коэффициент трения между столом и обручем равен m? Сколько оборотов N сделает обруч до полной остановки?
и положили (опустили) на горизонтальный стол. Через какое время t обруч остановится, если коэффициент трения между столом и обручем равен m? Сколько оборотов N сделает обруч до полной остановки?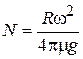 ;
;  )
) )
)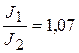 )
) )
)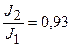 )
)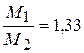 )
) = 5,9∙10-2 (кг∙м²)/с)
= 5,9∙10-2 (кг∙м²)/с)


