Примеры решения задач
 31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток
31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток 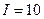 А. Найти магнитную индукцию
А. Найти магнитную индукцию 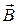 в точках М и N, если
в точках М и N, если  см.
см.
Дано:
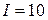 А А
 ,0 см = 5,0×10-2 м ,0 см = 5,0×10-2 м
| Решение
Величина магнитной индукции 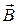 в точках М и N может быть найдена по принципу суперпозиции: в точках М и N может быть найдена по принципу суперпозиции:
|
а)  –?
б) –?
б)  –? –?
| 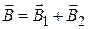 , (1) , (1)
|
 где
где 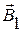 – магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Х;
– магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Х; 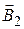 – магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Y. Модуль вектора магнитной индукции может быть рассчитан на основе закона Био – Савара – Лапласа. Нас интересует и будет использоваться результат расчета для прямолинейного отрезка проводника, представленного на рис. 2. Модуль вектора магнитной индукции в точке А на расстоянии b от отрезка проводника выражается формулой
– магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Y. Модуль вектора магнитной индукции может быть рассчитан на основе закона Био – Савара – Лапласа. Нас интересует и будет использоваться результат расчета для прямолинейного отрезка проводника, представленного на рис. 2. Модуль вектора магнитной индукции в точке А на расстоянии b от отрезка проводника выражается формулой
 , (2)
, (2)
где 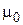 – магнитная постоянная,
– магнитная постоянная,  и
и 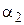 – углы между направлениями тока и направлениями радиус-векторов
– углы между направлениями тока и направлениями радиус-векторов 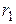 и
и 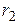 – начала и конца отрезка (см. рис. 2).
– начала и конца отрезка (см. рис. 2).
В точке М (см. рис. 1) вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Х, равен нулю ( ). Вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Y, характеризуется углами
). Вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Y, характеризуется углами 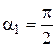 и
и 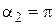 . Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции
. Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции  в точке М:
в точке М:
 мкТл.
мкТл.
Направление вектора 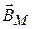 определяется правилом правого винта и показано на рис. 1.
определяется правилом правого винта и показано на рис. 1.
В точке N, как это следует из правила правого винта, вектора  и
и 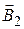 направлены вдоль одной линии перпендикулярно плоскости рис. 1. Поэтому модуль вектора магнитной индукции в точке N равен сумме модулей векторов
направлены вдоль одной линии перпендикулярно плоскости рис. 1. Поэтому модуль вектора магнитной индукции в точке N равен сумме модулей векторов  и
и  . Для величины магнитной индукции
. Для величины магнитной индукции  , как следует из рис. 1, угол
, как следует из рис. 1, угол  равен нулю, а угол
равен нулю, а угол 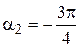 . Для величины
. Для величины  магнитной индукции, как следует из рис.1, угол
магнитной индукции, как следует из рис.1, угол 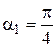 , а угол
, а угол 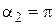 . Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции
. Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции  в точке N равен:
в точке N равен:
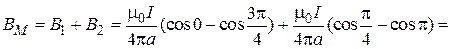
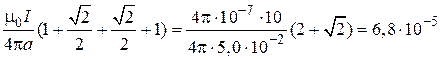 Тл
Тл 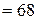 мкТл.
мкТл.
Направление вектора  определяется правилом правого винта и показано на рис.1.
определяется правилом правого винта и показано на рис.1.
Ответ: а) 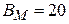 мкТл; б)
мкТл; б)  мкТл.
мкТл.
32. Тонкое кольцо радиусом 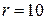 см заряжено равномерно с линейной плотностью заряда
см заряжено равномерно с линейной плотностью заряда 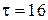 нКл/м. Кольцо вращается с частотой
нКл/м. Кольцо вращается с частотой 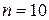 об/c. относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент
об/c. относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент 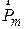 , обусловленный вращением кольца.
, обусловленный вращением кольца.
Дано:
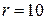 см см
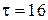 нКл/м нКл/м
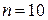 об/c об/c
| Решение:
Вращение заряженного кольца представляет собой круговой ток. Круговой ток создает в пространстве магнитный момент, величина модуля которого определяется выражением:
|
 –? –?
| 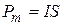 , ,
|
где 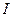 – сила кругового тока;
– сила кругового тока; 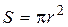 – площадь контура (кольца).
– площадь контура (кольца).
Сила кругового тока характеризуется количеством заряда, пересекающего площадку, перпендикулярную линии кольца в единицу времени. Поэтому для силы тока получается:, где – заряд кольца.
Таким образом модуль магнитного момента:  Направление вектора
Направление вектора  определяется правилом правого винта. Поэтому вектор
определяется правилом правого винта. Поэтому вектор  направлен по оси кольца и его направление совпадает с направлением вектора угловой скорости вращения кольца.
направлен по оси кольца и его направление совпадает с направлением вектора угловой скорости вращения кольца.
Ответ: 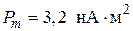
33. Длинный прямой соленоид с сердечником намотан из проволоки диаметром 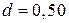 мм так, что витки плотно прилегают друг к другу. Найти напряженность магнитного поля внутри соленоида при силе тока
мм так, что витки плотно прилегают друг к другу. Найти напряженность магнитного поля внутри соленоида при силе тока  А. Магнитную проницаемость
А. Магнитную проницаемость 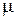 сердечника соленоида при данной силе тока принять равной 800.
сердечника соленоида при данной силе тока принять равной 800.
Дано:
 мм мм

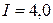 А А
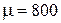
| Решение
Для длинного прямого соленоида можно пренебречь краевыми эффектами, и модуль напряженности  внутри соленоида определяется формулой внутри соленоида определяется формулой
|
а)  –?
б) –?
б)  –? –?
| 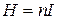 , (1) , (1)
|
где 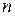 – число витков соленоида, приходящееся на единицу его длины. Так как витки плотно прилегают друг к другу, то их число на единицу длины
– число витков соленоида, приходящееся на единицу его длины. Так как витки плотно прилегают друг к другу, то их число на единицу длины
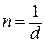 . (2)
. (2)
Из формул (1) и (2) для модуля напряженности  имеем
имеем
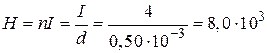 А/м.
А/м.
Вектор 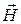 направлен параллельно оси соленоида.
направлен параллельно оси соленоида.
Как известно, вектор магнитной индукции 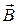 связан с вектором напряженности магнитного поля
связан с вектором напряженности магнитного поля 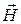 соотношением
соотношением
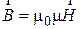 (3)
(3)
Из условия задачи и выражения (3) для магнитной индукции внутри соленоида получим 
Вектор 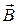 направлен параллельно оси соленоида.
направлен параллельно оси соленоида.
Ответ: 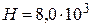 А/м;
А/м; 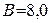 Тл.
Тл.
34. Тороид с сердечником, длина которого по средней линии  м, имеет воздушный зазор шириной
м, имеет воздушный зазор шириной  мм. Обмотка тора равномерно распределена по всей его длине с числом витков на единицу длины
мм. Обмотка тора равномерно распределена по всей его длине с числом витков на единицу длины  см-1. Найти силу тока
см-1. Найти силу тока  в обмотке, при которой магнитная индукция в зазоре будет равна
в обмотке, при которой магнитная индукция в зазоре будет равна  Тл. Магнитную проницаемость
Тл. Магнитную проницаемость 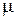 сердечника тороида при данной силе тока принять равной 800.
сердечника тороида при данной силе тока принять равной 800.
Дано:
 ,0 м ,0 м
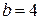 ,0 мм ,0 мм
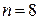 ,0 см-1 ,0 см-1
 Тл Тл
| Решение
По теореме о циркуляции вектора напряженности магнитного поля 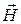 можно записать можно записать
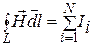 , (1)
где , (1)
где  – макроскопические точки, охватываемые контуром. – макроскопические точки, охватываемые контуром.
|
 –? –?
| Для тороида по средней линии левая часть формулы (1)
принимает вид
|

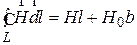 , (2)
, (2)
где  – напряженность магнитного поля в сердечнике;
– напряженность магнитного поля в сердечнике; 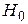 – напряженность магнитного поля в воздушном зазоре. Правая часть выражения (1) в случае тороида с обмоткой принимает форму
– напряженность магнитного поля в воздушном зазоре. Правая часть выражения (1) в случае тороида с обмоткой принимает форму
 , (3)
, (3)
где  – число витков всей обмотки тора.
– число витков всей обмотки тора.
Величины напряженностей магнитного поля  и
и 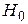 , в случае пренебрежения рассеянием магнитного потока связаны с магнитной индукцией
, в случае пренебрежения рассеянием магнитного потока связаны с магнитной индукцией  известными соотношениями:
известными соотношениями:
 , (4)
, (4)
 . (5)
. (5)
Приравнивая выражения (2) и (3) с использованием формул (4) и (5), для силы тока 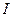 получим
получим
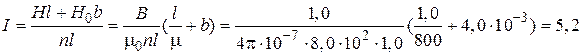 А.
А.
Ответ:  А.
А.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.23. Ток силы I = 1,0 А циркулирует в контуре, имеющем форму равнобочной трапеции. Отношение оснований трапеции h = 2: 1. Найти магнитную индукцию 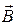 в точке А, лежащей в плоскости трапеции (см. рисунок). Меньшее основание трапеции d = 100 мм, расстояние b = 50 мм.
в точке А, лежащей в плоскости трапеции (см. рисунок). Меньшее основание трапеции d = 100 мм, расстояние b = 50 мм.
 (B =
(B =  = 1,4 мкТл)
= 1,4 мкТл)
d A
b
3.24. В тонком проводнике, изогнутом в виде правильного шестиугольника со стороной а = 20 см, идет ток I = 10 А. Определить магнитную индукцию в центре шестиугольника.
(B = 35×10-6 Тл)
3.25. Оценить индукцию магнитного поля В, создаваемого электроном в центре атома водорода, при движении электрона по первой боровской орбите, радиус которой а = 0,53×10-10 м.
(12,5 Тл)
3.26. По витку радиусом R = 10 см течет ток I = 50 А. Виток помещен в однородное магнитное поле В = 0,20 Тл. Определить момент силы М, действующей на виток, если плоскость витка составляет угол j = 60° с линиями индукции.
(0,16 Н×м)
3.27. Обмотка соленоида содержит два слоя плотно прилегающих друг к другу витков провода диаметром d = 0,20 мм. Определить магнитную индукцию на оси соленоида, если по проводу течет ток I = 0,50 А.
(6,3 мТл)
3.28. По тонкому стержню длиной l = 40 см равномерно распределен заряд Q = 60 нКл. Стержень вращается с частотой n = 12 с-1 относительно оси, перпендикулярной стержню и проходящей через стержень на расстоянии а = l /3 от одного из его концов. Определить магнитный момент Pm, обусловленный вращением стержня.
(4,0×10-8 А×м2)
3.29. Заряд Q = 0,10 мкКл равномерно распределен по стержню длиной l = 50 см. Стержень вращается с угловой скоростью w = 50 рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Найти магнитный момент Pm, обусловленный вращением стержня.
(5,2×10-8 А×м2)
3.30. В одной плоскости с бесконечно длинным прямым проводом, по которому течет ток I = 50 А, расположена прямоугольная рамка так, что две большие стороны её длиной l = 65 см параллельны проводу, а расстояние от провода до ближайшей из этих сторон равно её ширине. Каков магнитный поток j, пронизывающий рамку?
(4,5×10-6 Вб)
3.31. Стержень длиной l = 20 см заряжен равномерно распределенным зарядом с линейной плотностью t = 0,20 мкКл/м. Стержень вращается с частотой n = 10 с-1 относительно оси, перпендикулярной стержню и проходящей через его конец. Определить магнитный момент Pm, обусловленный вращением стержня.
(Pm = 1,7×10-8 А×м2)
3.32. Диск с равномерно распределенным по его плоскости зарядом Q равномерно вращается вокруг оси, проходящей через центр диска перпендикулярно его плоскости с частотой n. Радиус диска R. Найти магнитный момент диска относительно оси z.
(Pm = (1/2) Q p nR 2 А×м2)
3.33. Чугунное кольцо имеет воздушный зазор длиной l 0 = 5,0 мм. Длина l средней линии кольца равна 1,0 м. Сколько витков N содержит обмотка на кольце, если при силе тока I = 4,0 А индукция В магнитного поля в воздушном зазоре 0,50 Тл? Напряженность поля в металле Н = 1,5×103 А/м. Рассеянием магнитного потока в воздушном зазоре пренебречь.
(N = 8,7×102)
3.34. На сердечнике в виде тора диаметром d = 500 мм имеется обмотка с числом витков N = 1000. В сердечнике сделана поперечная прорезь, в результате чего образовался воздушный зазор ширины b = 1,0 мм. При силе тока в обмотке I = 0,85 А напряженность поля в зазоре Н = 600 кА/м. Определить магнитную проницаемость m железа при этих условиях. Рассеянием поля у краев зазора пренебречь.
(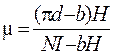 = 3,8×103)
= 3,8×103)
3.35. Тонкий металлический стержень длиной l = 1,2 м вращается с частотой n = 120 мин-1 в однородном магнитном поле вокруг оси, перпендикулярной к стержню и отстоящей от одного из его концов на расстоянии l 1 = 0,25 м. Вектор 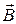 параллелен оси вращения, В = 0,10 мТл. Найти разность потенциалов I, возникающую между концами стержня. Выполните рисунок, поясняющей решение задачи.
параллелен оси вращения, В = 0,10 мТл. Найти разность потенциалов I, возникающую между концами стержня. Выполните рисунок, поясняющей решение задачи.
(0,53 мВ)
3.36. В магнитное поле, изменяющееся по закону 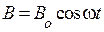 (Во = 0,10 Тл,
(Во = 0,10 Тл, 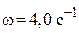 ), помещена квадратная рамка со стороной а = 50 см, причём нормаль к рамке образует с направлением поля угол a = 45°. Определите ЭДС индукции, возникающую в рамке в момент времени t = 5,0 с.
), помещена квадратная рамка со стороной а = 50 см, причём нормаль к рамке образует с направлением поля угол a = 45°. Определите ЭДС индукции, возникающую в рамке в момент времени t = 5,0 с.
( )
)
3.37. Электрон движется в однородном магнитном поле, индукция которого 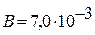 Тл, по окружности радиусом R = 3,0 см. Определить скорость и энергию электрона, а также цилиндрическую (ларморову) частоту его вращения.
Тл, по окружности радиусом R = 3,0 см. Определить скорость и энергию электрона, а также цилиндрическую (ларморову) частоту его вращения.
(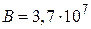 м/с;
м/с; 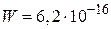 Дж;
Дж; 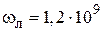 рад/с)
рад/с)
3.38. Электрон, обладая скоростью 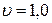 мм/с, влетает в однородное магнитное поле под углом
мм/с, влетает в однородное магнитное поле под углом  к направлению поля и начинает двигаться по спирали. Напряженность магнитного поля
к направлению поля и начинает двигаться по спирали. Напряженность магнитного поля  кА/м. Определите 1) шаг спирали; 2) радиус витка спирали. Изобразите качественно траекторию электрона в магнитном поле.
кА/м. Определите 1) шаг спирали; 2) радиус витка спирали. Изобразите качественно траекторию электрона в магнитном поле.
(1) 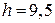 мм; 2)
мм; 2) 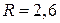 мм)
мм)
3.39. Катушку индуктивностью  Гн подключают к источнику тока. Определите сопротивление катушки, если за время
Гн подключают к источнику тока. Определите сопротивление катушки, если за время 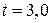 с сила тока через катушку достигает 80 % предельного значения. Постройте график зависимости силы тока (в относительных единицах силы тока) от времени.
с сила тока через катушку достигает 80 % предельного значения. Постройте график зависимости силы тока (в относительных единицах силы тока) от времени.
(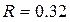 Ом)
Ом)
3.40. Определите, через сколько времени сила тока замыкания достигнет 0,95 предельного значения, если источник тока замыкают на катушку сопротивлением  Ом и индуктивностью 0,50 Гн. Постройте график зависимости силы тока (в относительных единицах
Ом и индуктивностью 0,50 Гн. Постройте график зависимости силы тока (в относительных единицах  ) от времени.
) от времени.
( с)
с)

 31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток
31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток 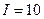 А. Найти магнитную индукцию
А. Найти магнитную индукцию 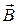 в точках М и N, если
в точках М и N, если  см.
см.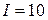 А
А
 ,0 см = 5,0×10-2 м
,0 см = 5,0×10-2 м
 –?
б)
–?
б)  –?
–?
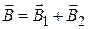 , (1)
, (1)
 где
где 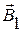 – магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Х;
– магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Х; 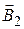 – магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Y. Модуль вектора магнитной индукции может быть рассчитан на основе закона Био – Савара – Лапласа. Нас интересует и будет использоваться результат расчета для прямолинейного отрезка проводника, представленного на рис. 2. Модуль вектора магнитной индукции в точке А на расстоянии b от отрезка проводника выражается формулой
– магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Y. Модуль вектора магнитной индукции может быть рассчитан на основе закона Био – Савара – Лапласа. Нас интересует и будет использоваться результат расчета для прямолинейного отрезка проводника, представленного на рис. 2. Модуль вектора магнитной индукции в точке А на расстоянии b от отрезка проводника выражается формулой , (2)
, (2)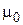 – магнитная постоянная,
– магнитная постоянная,  и
и 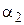 – углы между направлениями тока и направлениями радиус-векторов
– углы между направлениями тока и направлениями радиус-векторов 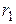 и
и 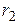 – начала и конца отрезка (см. рис. 2).
– начала и конца отрезка (см. рис. 2). ). Вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Y, характеризуется углами
). Вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Y, характеризуется углами 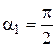 и
и 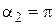 . Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции
. Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции  в точке М:
в точке М: мкТл.
мкТл.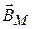 определяется правилом правого винта и показано на рис. 1.
определяется правилом правого винта и показано на рис. 1. и
и  и
и  . Для величины магнитной индукции
. Для величины магнитной индукции 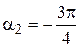 . Для величины
. Для величины 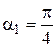 , а угол
, а угол 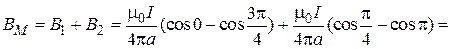
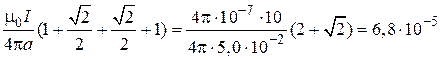 Тл
Тл 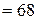 мкТл.
мкТл. определяется правилом правого винта и показано на рис.1.
определяется правилом правого винта и показано на рис.1.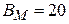 мкТл; б)
мкТл; б)  мкТл.
мкТл.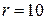 см заряжено равномерно с линейной плотностью заряда
см заряжено равномерно с линейной плотностью заряда 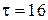 нКл/м. Кольцо вращается с частотой
нКл/м. Кольцо вращается с частотой 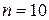 об/c. относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент
об/c. относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент 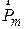 , обусловленный вращением кольца.
, обусловленный вращением кольца.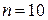 об/c
об/c
 –?
–?
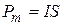 ,
,
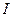 – сила кругового тока;
– сила кругового тока; 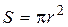 – площадь контура (кольца).
– площадь контура (кольца). Направление вектора
Направление вектора  определяется правилом правого винта. Поэтому вектор
определяется правилом правого винта. Поэтому вектор 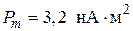
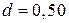 мм так, что витки плотно прилегают друг к другу. Найти напряженность магнитного поля внутри соленоида при силе тока
мм так, что витки плотно прилегают друг к другу. Найти напряженность магнитного поля внутри соленоида при силе тока  А. Магнитную проницаемость
А. Магнитную проницаемость 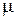 сердечника соленоида при данной силе тока принять равной 800.
сердечника соленоида при данной силе тока принять равной 800. мм
мм

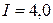 А
А
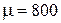
 внутри соленоида определяется формулой
внутри соленоида определяется формулой
 –?
–?
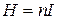 , (1)
, (1)
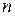 – число витков соленоида, приходящееся на единицу его длины. Так как витки плотно прилегают друг к другу, то их число на единицу длины
– число витков соленоида, приходящееся на единицу его длины. Так как витки плотно прилегают друг к другу, то их число на единицу длины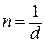 . (2)
. (2)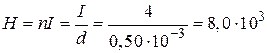 А/м.
А/м.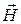 направлен параллельно оси соленоида.
направлен параллельно оси соленоида.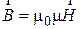 (3)
(3)
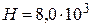 А/м;
А/м; 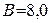 Тл.
Тл. м, имеет воздушный зазор шириной
м, имеет воздушный зазор шириной  мм. Обмотка тора равномерно распределена по всей его длине с числом витков на единицу длины
мм. Обмотка тора равномерно распределена по всей его длине с числом витков на единицу длины  см-1. Найти силу тока
см-1. Найти силу тока  в обмотке, при которой магнитная индукция в зазоре будет равна
в обмотке, при которой магнитная индукция в зазоре будет равна  Тл. Магнитную проницаемость
Тл. Магнитную проницаемость  ,0 м
,0 м
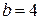 ,0 мм
,0 мм
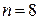 ,0 см-1
,0 см-1
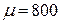
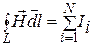 , (1)
где
, (1)
где  – макроскопические точки, охватываемые контуром.
– макроскопические точки, охватываемые контуром.

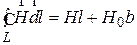 , (2)
, (2)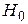 – напряженность магнитного поля в воздушном зазоре. Правая часть выражения (1) в случае тороида с обмоткой принимает форму
– напряженность магнитного поля в воздушном зазоре. Правая часть выражения (1) в случае тороида с обмоткой принимает форму , (3)
, (3) – число витков всей обмотки тора.
– число витков всей обмотки тора. и
и  известными соотношениями:
известными соотношениями: , (4)
, (4) . (5)
. (5)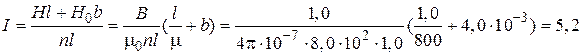 А.
А. А.
А.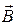 в точке А, лежащей в плоскости трапеции (см. рисунок). Меньшее основание трапеции d = 100 мм, расстояние b = 50 мм.
в точке А, лежащей в плоскости трапеции (см. рисунок). Меньшее основание трапеции d = 100 мм, расстояние b = 50 мм. (B =
(B =  = 1,4 мкТл)
= 1,4 мкТл)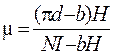 = 3,8×103)
= 3,8×103)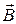 параллелен оси вращения, В = 0,10 мТл. Найти разность потенциалов I, возникающую между концами стержня. Выполните рисунок, поясняющей решение задачи.
параллелен оси вращения, В = 0,10 мТл. Найти разность потенциалов I, возникающую между концами стержня. Выполните рисунок, поясняющей решение задачи.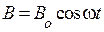 (Во = 0,10 Тл,
(Во = 0,10 Тл, 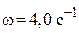 ), помещена квадратная рамка со стороной а = 50 см, причём нормаль к рамке образует с направлением поля угол a = 45°. Определите ЭДС индукции, возникающую в рамке в момент времени t = 5,0 с.
), помещена квадратная рамка со стороной а = 50 см, причём нормаль к рамке образует с направлением поля угол a = 45°. Определите ЭДС индукции, возникающую в рамке в момент времени t = 5,0 с. )
)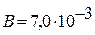 Тл, по окружности радиусом R = 3,0 см. Определить скорость и энергию электрона, а также цилиндрическую (ларморову) частоту его вращения.
Тл, по окружности радиусом R = 3,0 см. Определить скорость и энергию электрона, а также цилиндрическую (ларморову) частоту его вращения.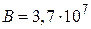 м/с;
м/с; 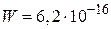 Дж;
Дж; 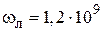 рад/с)
рад/с)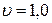 мм/с, влетает в однородное магнитное поле под углом
мм/с, влетает в однородное магнитное поле под углом  к направлению поля и начинает двигаться по спирали. Напряженность магнитного поля
к направлению поля и начинает двигаться по спирали. Напряженность магнитного поля  кА/м. Определите 1) шаг спирали; 2) радиус витка спирали. Изобразите качественно траекторию электрона в магнитном поле.
кА/м. Определите 1) шаг спирали; 2) радиус витка спирали. Изобразите качественно траекторию электрона в магнитном поле.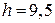 мм; 2)
мм; 2) 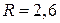 мм)
мм) Гн подключают к источнику тока. Определите сопротивление катушки, если за время
Гн подключают к источнику тока. Определите сопротивление катушки, если за время 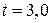 с сила тока через катушку достигает 80 % предельного значения. Постройте график зависимости силы тока (в относительных единицах силы тока) от времени.
с сила тока через катушку достигает 80 % предельного значения. Постройте график зависимости силы тока (в относительных единицах силы тока) от времени.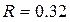 Ом)
Ом) Ом и индуктивностью 0,50 Гн. Постройте график зависимости силы тока (в относительных единицах
Ом и индуктивностью 0,50 Гн. Постройте график зависимости силы тока (в относительных единицах  ) от времени.
) от времени. с)
с)


