Механические колебания и волны
Пример решения задачи
35. Вдоль шнура распространяется поперечная волна, уравнение которой имеет вид Найти: а) период колебания точек шнура
где Период колебания
Волновое число определяется выражением Поэтому для скорости распространения волны
По найденным значениям периода колебаний Разность фаз колебаний любых двух точек шнура определяется формулой
Поэтому для точек шнура из условия задачи имеем
Скорость смещения точек шнура в поперечном направлении получается дифференцированием по времени выражения (1), т.е.
Из условия задачи и формулы (2) для максимального значения скорости Ответ: а) ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 4.1. Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние l = l/12, для момента времени t = T /6. Амплитуда колебания А = 0,050 м. (0,043 м)
4.2. Амплитуда гармонического колебания 5,0 см, период 4,0 с. Найти максимальную скорость колеблющейся точки и ее максимальное ускорение. (
4.3. Уравнение плоской волны имеет вид y = 0,34×cos(0,20 t – 0,40 x), где y – смещение частиц среды, и все числовые значения заданы в системе СИ. Записать числовые значения частоты и периода колебаний, волнового числа, фазовой скорости и длины волны, а также максимальное значение смещения. (
4.4. Поперечная волна распространяется вдоль упругого шнура со скоростью (200°)
4.5. Материальная точка совершает гармонические колебания согласно уравнению (Т = 2 с;
4.6. Период затухающих колебаний Т = 4,0 с; логарифмический декремент затухания ( 4.7. Поперечная волна, распространяясь вдоль упругого шнура, описывается уравнением
|

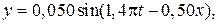 м, где
м, где  – смещение точек шнура;
– смещение точек шнура; 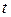 – время, с;
– время, с;  – координата точек шнура, м.
– координата точек шнура, м.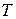 ; б) скорость распространения волны
; б) скорость распространения волны 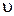 ; в) длину волны
; в) длину волны  ; г) разность фаз колебаний
; г) разность фаз колебаний  точек шнура, находящихся на расстоянии
точек шнура, находящихся на расстоянии  м; д) амплитуду скорости
м; д) амплитуду скорости  поперечного движения частиц шнура.
поперечного движения частиц шнура.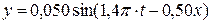 м
м
 ,0 м
,0 м
 –?;
г)
–?;
г) 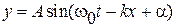 , (1)
, (1)
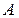 - амплитуда смещения,
- амплитуда смещения, 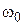 – циклическая частота,
– циклическая частота,  – волновое число,
– волновое число,  – начальная фаза. Из сравнения условий задачи и выражения (1) можно найти искомые величины.
– начальная фаза. Из сравнения условий задачи и выражения (1) можно найти искомые величины.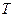 вязан с циклической частотой соотношением:
вязан с циклической частотой соотношением: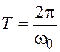 . Поэтому
. Поэтому 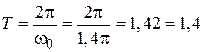 с.
с.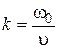 .
.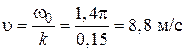
 можно определить длину волны из соотношения
можно определить длину волны из соотношения 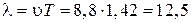 м.
м.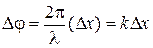 .
. рад.
рад. (2)
(2)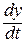 получается:
получается: 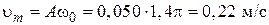
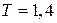 с; б)
с; б)  м/с; в)
м/с; в) 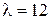 м; г)
м; г) 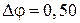 рад; д)
рад; д) 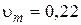 м/с.
м/с. = 7,8·10-2 м/с; am = 0,12 м/с2)
= 7,8·10-2 м/с; am = 0,12 м/с2) = 0,50 м/с; l = 16 м)
= 0,50 м/с; l = 16 м)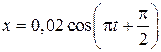 м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу; 4) максимальную скорость точки; 5) максимальное ускорение; 6) через сколько времени после начала отсчета точка будет проходить положение равновесия.
м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу; 4) максимальную скорость точки; 5) максимальное ускорение; 6) через сколько времени после начала отсчета точка будет проходить положение равновесия.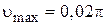 м/c;
м/c; 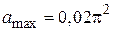
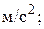
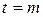
 )
) начальная фаза
начальная фаза  При t = T /8 смещение точки х = 4,5 см. Написать уравнение этого колебания. Построить график этого колебания в пределах двух периодов.
При t = T /8 смещение точки х = 4,5 см. Написать уравнение этого колебания. Построить график этого колебания в пределах двух периодов. см)
см) м. Определите: длину волны, фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии
м. Определите: длину волны, фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии 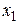 = 9 м от источника колебаний в момент времени
= 9 м от источника колебаний в момент времени 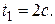 (
(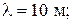



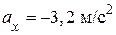 )
)


