Комбинирование обратного распространения с обучением Коши

Коррекция весов в комбинированном алгоритме, использующем обратное распространение и обучение Коши, состоит из двух компонент: (1) направленной компоненты, вычисляемой с использованием алгоритма обратного распространения, и (2) случайной компоненты, определяемой распределением Коши.

Эти компоненты вычисляются для каждого веса, и их сумма является величиной, на которую изменяется вес. Как и в алгоритме Коши, после вычисления изменения веса вычисляется целевая функция. Если имеет место улучшение, изменение сохраняется. В противном случае оно сохраняется с вероятностью, определяемой распределением Больцмана.

Коррекция веса вычисляется с использованием представленных ранее уравнений для каждого из алгоритмов:

w _mn,k(n+1) = w _mn,k(n) + η [aΔ w _mn,k(n) + (1 – a) δ_n,k OUT_m,j] + (1 – η) x _с,

где η – коэффициент, управляющий относительными величинами Коши и обратного распространения в компонентах весового шага. Если η приравнивается нулю, система становится полностью машиной Коши. Если η приравнивается единице, система становится машиной обратного распространения.

Изменение лишь одного весового коэффициента между вычислениями весовой функции неэффективно. Оказалось, что лучше сразу изменять все веса целого слоя, хотя для некоторых задач может оказаться выгоднее иная стратегия.

Преодоление сетевого паралича комбинированным методом обучения. Как и в машине Коши, если изменение веса ухудшает целевую функцию, – с помощью распределения Больцмана решается, сохранить ли новое значение веса или восстановить предыдущее значение. Таким образом, имеется конечная вероятность того, что ухудшающее множество приращений весов будет сохранено. Так как распределение Коши имеет бесконечную дисперсию (диапазон изменения тангенса простирается от – ¥ до + ¥ на области определения), то весьма вероятно возникновение больших приращений весов, часто приводящих к сетевому параличу.

Очевидное решение, состоящее в ограничении диапазона изменения весовых шагов, ставит вопрос о математической корректности полученного таким образом алгоритма. В работе [6] доказана сходимость системы к глобальному минимуму лишь для исходного алгоритма. Подобного доказательства при искусственном ограничении размера шага не существует. В действительности экспериментально выявлены случаи, когда для реализации некоторой функции требуются большие веса, и два больших веса, вычитаясь, дают малую разность.

Другое решение состоит в рандомизации весов тех нейронов, которые оказались в состоянии насыщения. Недостатком его является то, что оно может серьезно нарушить обучающий процесс, иногда затягивая его до бесконечности.

Для решения проблемы паралича был найден метод, не нарушающий достигнутого обучения. Насыщенные нейроны выявляются с помощью измерения их сигналов OUT. Когда величина OUT приближается к своему предельному значению, положительному или отрицательному, на веса, питающие этот нейрон, действует сжимающая функция. Она подобна используемой для получения нейронного сигнала OUT, за исключением того, что диапазоном ее изменения является интервал (+5,–5) или другое подходящее множество. Тогда модифицированные весовые значения равны

.

Эта функция сильно уменьшает величину очень больших весов, воздействие на малые веса значительно более слабое. Далее она поддерживает симметрию, сохраняя небольшие различия между большими весами. Экспериментально было показано, что эта функция выводит нейроны из состояния насыщения без нарушения достигнутого в сети обучения. Не было затрачено серьезных усилий для оптимизации используемой функции, другие значения констант могут оказаться лучшими.

Экспериментальное результаты. Комбинированный алгоритм, использующий обратное распространение и обучение Коши, применялся для обучения нескольких больших сетей. Например, этим методом была успешно обучена система, распознающая рукописные китайские иероглифы [б]. Все же время обучения может оказаться большим (приблизительно 36 часов машинного времени уходило на обучение).

В другом эксперименте эта сеть обучалась на задаче ИСКЛЮЧАЮЩЕЕ ИЛИ, которая была использована в качестве теста для сравнения с другими алгоритмами. Для сходимости сети в среднем требовалось около 76 предъявлении обучающего множества. В качестве сравнения можно указать, что при использовании обратного распространения в среднем требовалось около 245 предъявлении для решения этой же задачи [5] и 4986 итераций при использовании обратного распространения второго порядка.

Ни одно из обучений не привело к локальному минимуму, о которых сообщалось в [5]. Более того, ни одно из 160 обучений не обнаружило неожиданных патологий, сеть всегда правильно обучалась.

Эксперименты же с чистой машиной Коши привели к значительно большим временам обучения. Например, при r = 0,002 для обучения сети в среднем требовалось около 2284 предъявлении обучающего множества.
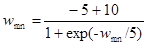