ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ВЫСШЕГО ПОРЯДКА
Так же, как и для случая первой производной, введем итерационный оператор разностей
Пример
Стоящие в правой части выражения (16) члены представляют собой биномиальные коэффициенты, которые представляются в общем виде с помощью выражения
Тогда формула для вычисления
Доказательство формулы (18) очевидно и вытекает из многократного дифференцирования (15). Запишем два важных частных случая формулы (18) для
и
Следовательно,  -ая производная кривой Безье в крайних точках дуги зависит только от -ая производная кривой Безье в крайних точках дуги зависит только от 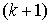 ближайших управляющих точек, включая саму крайнюю точку. Для ближайших управляющих точек, включая саму крайнюю точку. Для  очевидно, что векторы очевидно, что векторы  и и 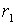 определяют касательную в точке с параметром определяют касательную в точке с параметром  . В общем случае касательная в точке . В общем случае касательная в точке  определяется вектором определяется вектором  и первым вектором и первым вектором  , отличным от , отличным от  . Таким образом, касательная в точке . Таким образом, касательная в точке  может быть определена даже в том случае, если касательный вектор равен нулю. Для другого конца дуги может быть определена даже в том случае, если касательный вектор равен нулю. Для другого конца дуги  рассуждения аналогичны. На рис. 14.3 показаны примеры определения векторов первой и второй производных в начальной точке дуги кривой. рассуждения аналогичны. На рис. 14.3 показаны примеры определения векторов первой и второй производных в начальной точке дуги кривой.
Рис. 14.3. - Определение векторов первой и второй производных
|

 , определяемый с помощью выражения
, определяемый с помощью выражения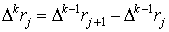
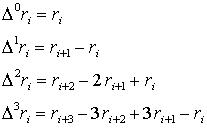 .
. .
.
 .
.
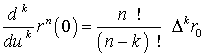
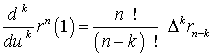 .
.





