МЕТОД БУЛЕВОЙ СУММЫ (поверхности Кунса)
В случае конструирования поверхности методом Кунса необходимо задать два семейства граничных кривых (в
Граничные кривые представляют собой рациональные кривые Безье, управляющие точки которых получены с помощью методов интерполяции исходных точек поверхности, внутренние точки порции поверхности вычисляются с помощью билинейной интерполяции в двух направлениях. Обобщением поверхностей Кунса являются поверхности, интерполирующие всю заданную криволинейную сетку При моделировании поверхностей с помощью рассмотренных методов предполагается, что исходные данные в виде массивов точек, характерных линий поверхности или определяющих их функций получены в результате физических экспериментов, решения прикладных задач, сняты с натурных макетов или выполнены дизайнерами. Для интерактивного конструирования и последующей модификации двумерных обводов наиболее приспособлены методы тензорного произведения, в которых в качестве базовых используются полиномы Бернштейна и связанные с ними методы построения характеристических сеток. В заключение отметим, что в ряде случаев для геометрического моделирования сложных криволинейных двумерных обводов целесообразно использовать топологически непрямоугольные (в частности треугольные) порции поверхностей. В этом случае математическое задание обводов производится с помощью обобщенных полиномов Бернштейна.
|

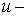 и
и 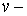 направлениях). Уравнение поверхности Кунса имеет вид
направлениях). Уравнение поверхности Кунса имеет вид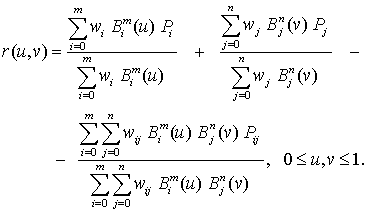
 (поверхности Гордона).
(поверхности Гордона).


