Итак, другой распространенной формой представления полиномов является представление в форме Бернштейна. Кроме аспектов, связанных с вычислительной устойчивостью алгоритмов с участием полиномов в форме Бернштейна, этот вид представления полиномов имеет несомненные преимущества чисто с геометрической точки зрения. Рассмотрим "геометрические" свойства полиномов Бернштейна более подробно.
Произвольный полином степени  в форме Бернштейна определяется уравнением
в форме Бернштейна определяется уравнением
 . .
| (11)
|
где 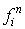 - коэффициенты Бернштейна,
- коэффициенты Бернштейна,
 - скалярные функции Бернштейна.
- скалярные функции Бернштейна.
Коэффициенты 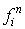 могут быть скалярными значениями некоторой функции
могут быть скалярными значениями некоторой функции  , вычисленными на некотором отрезке
, вычисленными на некотором отрезке 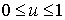 для равноотстоящих точек. Тогда полином
для равноотстоящих точек. Тогда полином 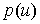 аппроксимирует функцию
аппроксимирует функцию  при достаточно больших
при достаточно больших  .
.
Если заменить скалярные коэффициенты 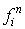 произвольными векторами
произвольными векторами 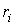 , то в этом случае полином
, то в этом случае полином 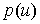 аппроксимирует ломаную, вершинами которой является заданный набор векторов
аппроксимирует ломаную, вершинами которой является заданный набор векторов 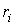 , и определяет на заданном отрезке
, и определяет на заданном отрезке 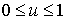 дугу кривой Безье
дугу кривой Безье  -го порядка. Изменяя положение векторов, можно управлять формой дуги кривой.
-го порядка. Изменяя положение векторов, можно управлять формой дуги кривой.
Скалярные функции  определяются уравнениями
определяются уравнениями

и образуют так называемый базис Бернштейна для множества всех полиномов степени не выше  на отрезке
на отрезке  . Например, для случая
. Например, для случая 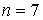 изображены функции базиса Бернштейна (см. рис. 14.1).
изображены функции базиса Бернштейна (см. рис. 14.1).

Рис. 14.1. Полиномы Бернштейна степени 7
В ряде случаев вместо единичного отрезка  изменения параметра целесообразно использовать отрезок
изменения параметра целесообразно использовать отрезок 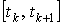 . Тогда значения локального параметра
. Тогда значения локального параметра  на этом общем отрезке
на этом общем отрезке 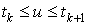 можно вычислить по формуле:
можно вычислить по формуле:
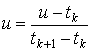 .
.
На отрезке 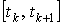 базисные функции Бернштейна определяются уравнениями
базисные функции Бернштейна определяются уравнениями

|
(12)
|
Отметим следующие основные свойства полиномов Бернштейна:
1. Сумма полиномов, определенных на заданном отрезке, равна единице:
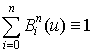 ,
,  .
.
Это свойство обеспечивает инвариантность полиномов при аффинных преобразованиях. Следовательно, аффинно-инвариантны и кривые Безье, определяемые этим набором полиномов. Заметим, что этим свойством обладают также полиномы в форме Лагранжа (8) и Эрмита (9), но не обладают стандартные полиномы (1).
Ø Все полиномы не отрицательны на заданном отрезке
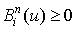 ,
,  .
.
В работе [3] указано, что значения полинома 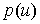 находятся в интервале
находятся в интервале
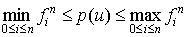 .
.
Это означает, что кривая, определяемая полиномом 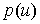 , лежит внутри выпуклой оболочки коэффициентов
, лежит внутри выпуклой оболочки коэффициентов 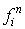 . Часто это свойство называют "свойством выпуклости оболочки". Заметим, что на плоскости выпуклая оболочка представляет собой область, ограниченную выпуклой ломаной, а в пространстве – выпуклым многогранником.
. Часто это свойство называют "свойством выпуклости оболочки". Заметим, что на плоскости выпуклая оболочка представляет собой область, ограниченную выпуклой ломаной, а в пространстве – выпуклым многогранником.
Ø Возможно рекурсивное вычисление полиномов степени  , если известны полиномы степени
, если известны полиномы степени  :
:
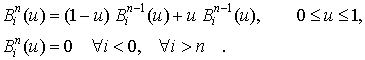
Это свойство используется для вычисления  с помощью повторяющейся линейной интерполяции.
с помощью повторяющейся линейной интерполяции.
1) Если 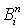 - полиномы Бернштейна степени
- полиномы Бернштейна степени  , то полиномы
, то полиномы 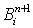 степени
степени 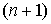 вычисляются с помощью выражения:
вычисляются с помощью выражения:
 ,
,
где  для
для 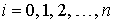 .
.
 ,
, 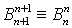 .
.
Это свойство используется при аппроксимации кривой Безье  -го порядка другой кривой порядка
-го порядка другой кривой порядка  .
.
В работе [2] доказано, что полиномы Бернштейна лучше приспособлены для вычисления простых корней, чем степенные полиномы, как на единичном отрезке  , так и на отрезке
, так и на отрезке  . Полиномы в форме Бернштейна обладают большей вычислительной устойчивостью, чем степенные полиномы. Это связано с тем, что при вычислении степенных полиномов по схеме Горнера может происходить значительная потеря точности за счет вычитания близких больших по модулю округленных чисел. При этом потеря точности увеличивается с возрастанием
. Полиномы в форме Бернштейна обладают большей вычислительной устойчивостью, чем степенные полиномы. Это связано с тем, что при вычислении степенных полиномов по схеме Горнера может происходить значительная потеря точности за счет вычитания близких больших по модулю округленных чисел. При этом потеря точности увеличивается с возрастанием  из-за ограниченного числа цифровых разрядов компьютера. Избежать потери точности в этом случае удается, применяя для вычисления полинома рекуррентные формулы. Один из методов измерения вычислительной устойчивости алгоритмов заключается в сравнении оценок погрешностей значения полинома в различных формах представления в окрестности произвольной точки [7]. В работе [5] выполнено исследование вычислительных аспектов алгоритмов полиномиальной аппроксимации и доказано, что полиномы в форме Бернштейна имеют меньшую оценку погрешности, чем степенные полиномы в стандартной форме. Однако при выполнении преобразования из одной формы представления полинома в другую указанное свойство может теряться из-за появления вычислительной неустойчивости.
из-за ограниченного числа цифровых разрядов компьютера. Избежать потери точности в этом случае удается, применяя для вычисления полинома рекуррентные формулы. Один из методов измерения вычислительной устойчивости алгоритмов заключается в сравнении оценок погрешностей значения полинома в различных формах представления в окрестности произвольной точки [7]. В работе [5] выполнено исследование вычислительных аспектов алгоритмов полиномиальной аппроксимации и доказано, что полиномы в форме Бернштейна имеют меньшую оценку погрешности, чем степенные полиномы в стандартной форме. Однако при выполнении преобразования из одной формы представления полинома в другую указанное свойство может теряться из-за появления вычислительной неустойчивости.
Полиномы Бернштейна 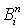 имеют максимум при значении параметра
имеют максимум при значении параметра  . Это свойство используется при локальном контроле формы обвода. Перемещение управляющей точки
. Это свойство используется при локальном контроле формы обвода. Перемещение управляющей точки  кривой Безье в большей мере затрагивает участок кривой в окрестности точки со значением параметра
кривой Безье в большей мере затрагивает участок кривой в окрестности точки со значением параметра 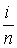 .
.
Полиномы Бернштейна могут быть вычислены по схеме Горнера с помощью следующих формул: 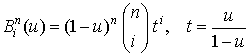 на отрезке
на отрезке 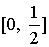 ;
;
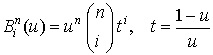 на отрезке
на отрезке  .
.

 в форме Бернштейна определяется уравнением
в форме Бернштейна определяется уравнением .
.
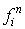 - коэффициенты Бернштейна,
- коэффициенты Бернштейна, - скалярные функции Бернштейна.
- скалярные функции Бернштейна. , вычисленными на некотором отрезке
, вычисленными на некотором отрезке 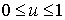 для равноотстоящих точек. Тогда полином
для равноотстоящих точек. Тогда полином 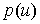 аппроксимирует функцию
аппроксимирует функцию 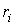 , то в этом случае полином
, то в этом случае полином 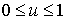 дугу кривой Безье
дугу кривой Безье 
 . Например, для случая
. Например, для случая 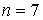 изображены функции базиса Бернштейна (см. рис. 14.1).
изображены функции базиса Бернштейна (см. рис. 14.1).
 изменения параметра целесообразно использовать отрезок
изменения параметра целесообразно использовать отрезок 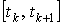 . Тогда значения локального параметра
. Тогда значения локального параметра  на этом общем отрезке
на этом общем отрезке 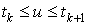 можно вычислить по формуле:
можно вычислить по формуле: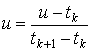 .
.
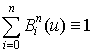 ,
,  .
.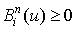 ,
, 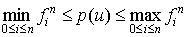 .
. :
: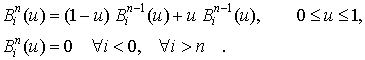
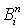 - полиномы Бернштейна степени
- полиномы Бернштейна степени 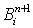 степени
степени 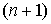 вычисляются с помощью выражения:
вычисляются с помощью выражения: ,
, для
для 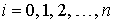 .
. ,
, 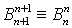 .
. .
. , так и на отрезке
, так и на отрезке  . Полиномы в форме Бернштейна обладают большей вычислительной устойчивостью, чем степенные полиномы. Это связано с тем, что при вычислении степенных полиномов по схеме Горнера может происходить значительная потеря точности за счет вычитания близких больших по модулю округленных чисел. При этом потеря точности увеличивается с возрастанием
. Полиномы в форме Бернштейна обладают большей вычислительной устойчивостью, чем степенные полиномы. Это связано с тем, что при вычислении степенных полиномов по схеме Горнера может происходить значительная потеря точности за счет вычитания близких больших по модулю округленных чисел. При этом потеря точности увеличивается с возрастанием  . Это свойство используется при локальном контроле формы обвода. Перемещение управляющей точки
. Это свойство используется при локальном контроле формы обвода. Перемещение управляющей точки  кривой Безье в большей мере затрагивает участок кривой в окрестности точки со значением параметра
кривой Безье в большей мере затрагивает участок кривой в окрестности точки со значением параметра 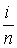 .
.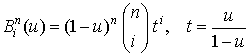 на отрезке
на отрезке 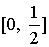 ;
;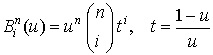 на отрезке
на отрезке  .
.


