СВОЙСТВА ОБОБЩЕННЫХ ПОЛИНОМОВ БЕРНШТЕЙНА
Треугольную порцию поверхности можно определить, используя обобщенные полиномы Бернштейна:
где
Сумма полиномов, определенных на заданном интервале, равна единице
Свойства обобщенных полиномов Бернштейна сходны со свойствами одномерных полиномов: 1. Сумма полиномов, определенных на заданном интервале, равна единице 2. Все полиномы положительны на заданном интервале
3. Возможно рекурсивное вычисление полиномов степени
Пример
Рис. 13.10. Формулы обобщенных кубических полиномов Бернштейна
Рис. 13.11. Семейство кубических обобщенных полиномов Бернштейна
Рис. 13.12. Примеры обобщенных кубических полиномов Бернштейна Мы рассмотрели алгоритм определения точки, инцидентной треугольной порции поверхности, с заданными барицентрическими координатами на основе повторяющейся линейной интерполяции. Решим эту задачу, используя обобщенные полиномы Бернштейна и их свойства. Запишем уравнение (10) в виде
Таким образом, каждый шаг алгоритма связан с линейной интерполяцией, определяемой формулой
Подставляя в уравнение (12)
или
Угловые точки порции поверхности задаются векторами Граничные кривые определяются характеристическими ломаными:
Так же, как и для одномерного случая, перемещение любой из управляющих точек
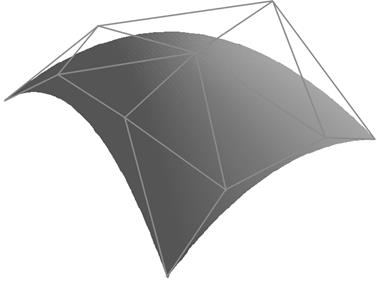
Рис. 13.13. Кубическая треугольная порция поверхности Безье и ее характеристический многогранник
|

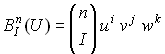 ,
,
 - барицентрические координаты,
- барицентрические координаты, ,
,  ,
, 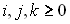 .
.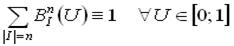 .
.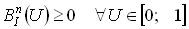 .
. , если известны полиномы степени
, если известны полиномы степени 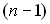 :
: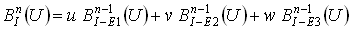 ,
, 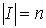 .
. и представим результаты в виде схемы (Рис. 10).
и представим результаты в виде схемы (Рис. 10). 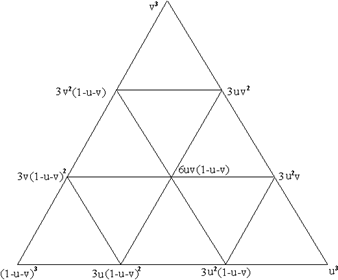







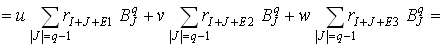
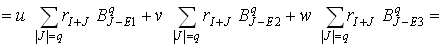
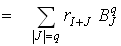 .
.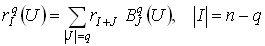 .
.
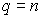 , получим уравнение треугольной порции поверхности Безье, определенной с помощью обобщенных полиномов Бернштейна:
, получим уравнение треугольной порции поверхности Безье, определенной с помощью обобщенных полиномов Бернштейна: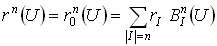
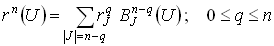 .
.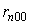 ,
,  и
и 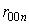 .
. ;
;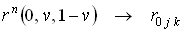 ;
;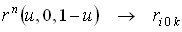 .
. влияет на форму поверхности в окрестности этой точки. Пример сконструированной кубической треугольной порции поверхности показан на рис. 13.13.
влияет на форму поверхности в окрестности этой точки. Пример сконструированной кубической треугольной порции поверхности показан на рис. 13.13.