АЛГОРИТМ ЗАДАНИЯ КВАДРАТИЧНОЙ ПАРАБОЛЫ
Рассмотрим простую схему конструирования квадратичной параболы, которую далее обобщим для кривых Безье произвольного порядка. Пусть
Подставляя первые два уравнения в третье, получим уравнение второго порядка относительно переменной
Таким образом, при изменении переменной
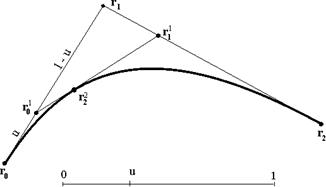
Анализируя расположение точек на рис. 13.4, можно отметить равенство отношений
Рис. 13.4. Конструирование параболы с использованием линейной интерполяции Так как кусочная линейная интерполяция аффинно инвариантна, то сконструированная парабола обладает таким же свойством. Можно также отметить, что данная кривая является плоским коническим сечением, поскольку любая точка на ней однозначно определяется заданием трех барицентрических координат. Прежде чем рассмотреть алгоритм Кастельжо для произвольной кривой, приведем теорему о трех касательных, полностью связанную с вышеприведенным конструированием параболы. Пусть
Рис. 13.5. Иллюстрация теоремы о трех касательных Проведем касательные Тогда справедливо равенство отношений Эта теорема определяет свойства квадратичной параболы. Теперь, учитывая конструктивные аналогии, рассмотрим алгоритм линейной интерполяции для произвольной кривой.
|

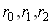 - три произвольные точки в пространстве
- три произвольные точки в пространстве 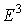 , и пусть
, и пусть 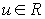 . Запишем следующие выражения:
. Запишем следующие выражения: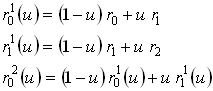 .
.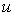 :
: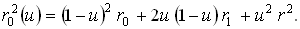
 до
до  уравнение (7) описывает параболу, которую мы будем обозначать
уравнение (7) описывает параболу, которую мы будем обозначать 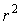 . Приведенные выше выражения представляют собой повторяющуюся линейную интерполяцию, иллюстрация которой приведена на рис. 4. При значениях переменной в интервале от 0 до 1 парабола
. Приведенные выше выражения представляют собой повторяющуюся линейную интерполяцию, иллюстрация которой приведена на рис. 4. При значениях переменной в интервале от 0 до 1 парабола 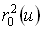 лежит внутри треугольника, образованного точками
лежит внутри треугольника, образованного точками 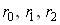 .
. 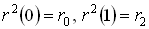 .
.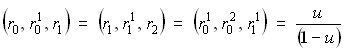 .
.
 - три действительные различные точки на параболе (рис. 13.5).
- три действительные различные точки на параболе (рис. 13.5).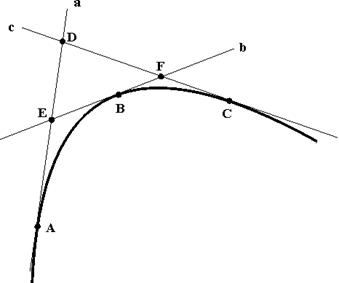
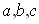 к параболе в этих точках. Обозначим точки пересечения касательных
к параболе в этих точках. Обозначим точки пересечения касательных 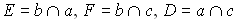 .
.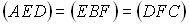 .
.


