Алгоритм
Для треугольной порции поверхности, ограниченной кривыми
Введем некоторые обозначения:
Произвольная точка с барицентрическими координатами
где Последний шаг алгоритма дает искомую точку Граничные кривые треугольной порции определяются соответствующими характеристическими ломаными. Одна из барицентрических координат произвольной точки на этих кривых равна 0. Подставим в уравнение (10) барицентрические координаты границ треугольной области:
Получим уравнения для определения точек на граничных кривых порции поверхности:
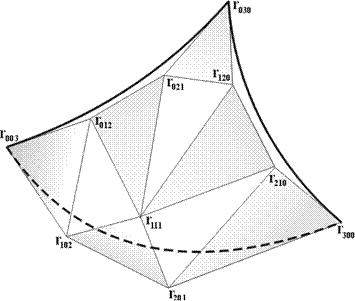
Сравнивая любое из полученных уравнений с уравнением (8), убеждаемся, что они эквивалентны. Следовательно, можно сделать вывод о том, что алгоритм, описываемый уравнением (10), является обобщением алгоритма для одномерного случая (8). Пример 1. Характеристический многогранник такой порции содержит 10 управляющих точек (рис. 13.7.):
2. Сумма всех индексов каждой управляющей точки равна 3:
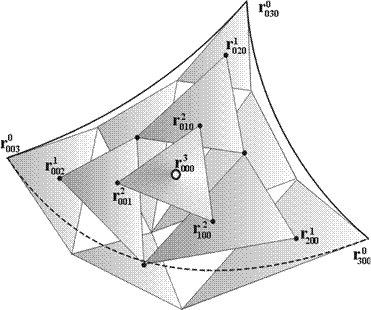
3. Подставляем эти значения в формулу (10). На рис. 9 показано формирование треугольных массивов управляющих точек на каждом шаге алгоритма. На рис. 9 иллюстрируется повторяющаяся линейная интерполяция трех точек. На последнем шаге алгоритма вычисляется радиус-вектор точки с заданными барицентрическими координатами, инцидентной треугольной кубической порции поверхности.
Рис. 13.7. Характеристический многогранник кубической треугольной порции поверхности
Рис. 13.8. Формирование треугольных массивов управляющих точек
Рис. 13.9. Иллюстрация работы алгоритма для треугольной кубической порции поверхности
|

 -го порядка, число точек характеристического
-го порядка, число точек характеристического  .
. ,
,  ,
, 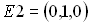 ,
, 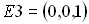 ,
,  ,
,  .
.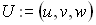 , инцидентная заданной порции поверхности, определяется с помощью повторяющейся линейной интерполяции каждых трех точек характеристического многогранника:
, инцидентная заданной порции поверхности, определяется с помощью повторяющейся линейной интерполяции каждых трех точек характеристического многогранника: ,
,
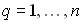 ,
, 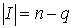 .
.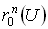 .
. ,
,  ,
,  .
. ,
,  .
. ,
, 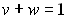 .
.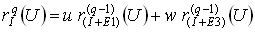 ,
,  .
.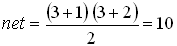 .
. ,
,  ,
, 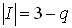 .
.