Приведенные выражения для квадратичной параболы легко обобщаются на случай произвольной пространственной кривой  -го порядка.
-го порядка.
Пусть  - произвольные точки в пространстве
- произвольные точки в пространстве 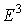 ,
, 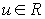 . Тогда для параболы
. Тогда для параболы  -го порядка запишем
-го порядка запишем
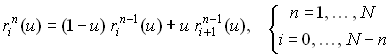
| (8)
|
Отметим, что  . Значение
. Значение 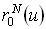 определяет точку со значением параметра
определяет точку со значением параметра 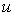 на кривой Безье
на кривой Безье 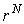 .
.
Ломаная 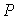 , образованная отрезками прямых, соединяющих точки
, образованная отрезками прямых, соединяющих точки  , называется ломаной Безье, или управляющей ломаной кривой
, называется ломаной Безье, или управляющей ломаной кривой 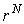 . Соответственно, вершины ломаной
. Соответственно, вершины ломаной 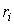 называются управляющими точками, или точками Безье.
называются управляющими точками, или точками Безье.
На рис. 6 показано определение точки на кубической кривой Безье с помощью алгоритма Кастельжо.
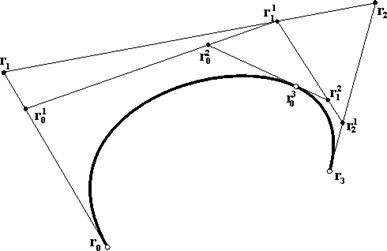
Рис. 13.6. Построение точки 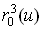 на кубической кривой с использованием повторяющейся линейной интерполяции
на кубической кривой с использованием повторяющейся линейной интерполяции
Промежуточные точки 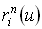 удобно записывать, используя схему Кастельжо, т.е. в виде треугольного массива.
удобно записывать, используя схему Кастельжо, т.е. в виде треугольного массива.
Например, для кубической кривой схема Кастельжо выглядит следующим образом:
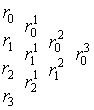
Произвольную точку кривой 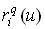 также можно вычислить с помощью полиномов Бернштейна:
также можно вычислить с помощью полиномов Бернштейна:
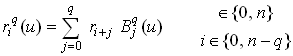
| (9)
|
Важно, что в случае 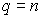 это уравнение дает точку на кривой:
это уравнение дает точку на кривой:
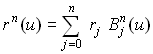 .
.
13.2.3. ОБОБЩЁННЫЙ АЛГОРИТМ ДЛЯ ТРЕУГОЛЬНОЙ ПОРЦИИ ПОВЕРХНОСТИ
Для определения точки, инцидентной треугольной порции поверхности, с заданными барицентрическими координатами используем обобщение линейной интерполяции для произвольной кривой  -го порядка.
-го порядка.
Дано: характеристический многогранник треугольной порции поверхности  и точка в пространстве
и точка в пространстве  , заданная барицентрическими координатами
, заданная барицентрическими координатами  .
.
Найти: точку, инцидентную заданной порции поверхности, с соответствующими барицентрическими координатами.

 -го порядка.
-го порядка. - произвольные точки в пространстве
- произвольные точки в пространстве 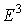 ,
, 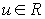 . Тогда для параболы
. Тогда для параболы 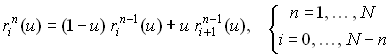
 . Значение
. Значение 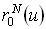 определяет точку со значением параметра
определяет точку со значением параметра 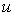 на кривой Безье
на кривой Безье 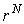 .
.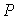 , образованная отрезками прямых, соединяющих точки
, образованная отрезками прямых, соединяющих точки 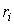 называются управляющими точками, или точками Безье.
называются управляющими точками, или точками Безье.
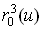 на кубической кривой с использованием повторяющейся линейной интерполяции
на кубической кривой с использованием повторяющейся линейной интерполяции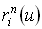 удобно записывать, используя схему Кастельжо, т.е. в виде треугольного массива.
удобно записывать, используя схему Кастельжо, т.е. в виде треугольного массива. 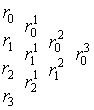
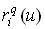 также можно вычислить с помощью полиномов Бернштейна:
также можно вычислить с помощью полиномов Бернштейна: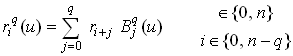
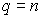 это уравнение дает точку на кривой:
это уравнение дает точку на кривой: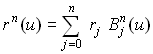 .
. и точка в пространстве
и точка в пространстве  , заданная барицентрическими координатами
, заданная барицентрическими координатами  .
.


