СВОЙСТВА ТРЕУГОЛЬНОЙ ПОРЦИИ ПОВЕРХНОСТИ БЕЗЬЕ
Треугольные порции поверхности являются естественным обобщением метода барицентрических координат на плоскости. Произвольная точка,инцидентная такой порции поверхности,может быть определена с помощью повторяющейся линейной интерполяции. Применяемые при этом алгоритмы линейной интерполяции являются обобщением алгоритмов для одномерного случая. Следовательно, сохранятся и важные свойства геометрических фигур, конструируемых с помощью линейной интерполяции. Отметим эти свойства конструируемых треугольных порций поверхности: 1. Поверхности в общем случае принадлежат только три точки характеристического многогранника с барицентрическими координатами (0, 0, 1), (0, 1, 0) и (1, 0, 0). 2. Аффинная инвариантность. Это свойство вытекает из того, что в алгоритме используется линейная интерполяция, являющаяся аффинным преобразованием пространства. 3. Инвариантность при аффинных преобразованиях параметра. 4. Треугольная порция поверхности лежит в выпуклой оболочке своего характеристического многогранника. Это свойство подтверждается тем, что любая точка 5. Образом произвольной прямой в плоскости параметров
|
, 
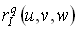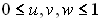определяется с помощью линейной комбинации предыдущих точек 
.
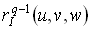является кривая 
-го порядка на треугольной порции поверхности [3]. Это весьма важное отличие треугольных порций от топологически прямоугольных порций поверхностей тензорного произведения.
