Теория приближения функций полиномами была разработана в трудах И. Ньютона, П.Л. Чебышева, К. Вейерштрасса, С.Н. Бернштейна и др. Чисто математические аспекты полиномиального приближения освещены достаточно подробно в многочисленной литературе по вычислительной математике и численным методам.
В общем случае в задачах геометрического моделирования сложных объектов проектируемые кривые не могут быть записаны в виде уравнения  с использованием обычных однозначных функций. Кривые инженерных объектов могут иметь вертикальные касательные, что тесно связано с многозначностью функций. Поэтому в автоматизированном проектировании ведущую роль играет параметрическое представление участков кривых.
с использованием обычных однозначных функций. Кривые инженерных объектов могут иметь вертикальные касательные, что тесно связано с многозначностью функций. Поэтому в автоматизированном проектировании ведущую роль играет параметрическое представление участков кривых.
Параметризация осуществляется заданием декартовых координат точки кривой как функций некоторого параметра:
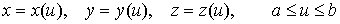 .
.
Для задания кривых используют параметрическое уравнение в векторной форме
 , где
, где  - радиус-вектор точки на кривой;
- радиус-вектор точки на кривой;
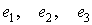 - орты координатных осей;
- орты координатных осей;
 - параметр точки на кривой.
- параметр точки на кривой.
В качестве параметра  выбирается переменная, относительно которой удобно будет задать искомые функции: длину дуги, номер узловых точек, полярный угол, параметр времени и др.
выбирается переменная, относительно которой удобно будет задать искомые функции: длину дуги, номер узловых точек, полярный угол, параметр времени и др.
Параметрический метод задания кривых имеет следующие преимущества:
более простое вычисление координат точек;
упрощение расчетов при преобразованиях кривых;
упрощение расчетов, связанных с подготовкой информации для станков с числовым программным управлением.
В геометрическом моделировании большое теоретическое и прикладное значение имеет разработка методов и алгоритмов проектирования сложных криволинейных обводов, описываемых параметрическими полиномами. При этом наиболее часто используется стандартная степенная форма (мономиальный базис) представления таких полиномов:

| (1)
|
В этой форме представления произвольный полином  -ой степени может быть легко вычислен по схеме Горнера, которая реализуется с помощью
-ой степени может быть легко вычислен по схеме Горнера, которая реализуется с помощью  умножений и
умножений и  сложений, т.е. всего за
сложений, т.е. всего за  арифметических действий. Схема Горнера удобна для реализации на компьютере благодаря цикличности вычислений и необходимости сохранять кроме коэффициентов полинома и значений аргумента только одной промежуточной величины. Полином
арифметических действий. Схема Горнера удобна для реализации на компьютере благодаря цикличности вычислений и необходимости сохранять кроме коэффициентов полинома и значений аргумента только одной промежуточной величины. Полином 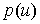 единственным образом разлагается в произведение из
единственным образом разлагается в произведение из  линейных множителей:
линейных множителей:
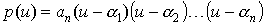 .
.
При решении прикладных задач в основном применяют полиномы с коэффициентами 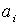 , являющимися вещественными числами. Решения
, являющимися вещественными числами. Решения  вещественного полинома обладают следующими свойствами:
вещественного полинома обладают следующими свойствами:
решения могут повторяться (например, если 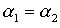 );
);
решения могут быть как вещественными, так и комплексными;
комплексные корни имеют сопряженные пары.
Как правило, из множества полиномов выбирают полиномы нечетных степеней. Это объясняется следующим. Если полином 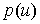 имеет нечетную степень, то он должен иметь, по крайней мере, один вещественный корень. Это вытекает непосредственно из приведенных выше свойств, т.к. общее число решений нечетного полинома – нечетное число, а комплексных корней (если они существуют) – четное число. Далее мы также будем рассматривать только вещественные полиномы.
имеет нечетную степень, то он должен иметь, по крайней мере, один вещественный корень. Это вытекает непосредственно из приведенных выше свойств, т.к. общее число решений нечетного полинома – нечетное число, а комплексных корней (если они существуют) – четное число. Далее мы также будем рассматривать только вещественные полиномы.
Итак, рассмотрим вектор-функцию в виде векторного полинома степени  :
:
 , ,  , ,
| (2)
|
где  - произвольные постоянные векторы;
- произвольные постоянные векторы;
 - интервал изменения параметра
- интервал изменения параметра  кривой
кривой 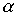 .
.
Пусть в 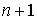 точках кривой
точках кривой 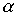 последовательно заданы значения радиус-вектора
последовательно заданы значения радиус-вектора 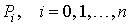 .
.
Назначим каждому значению радиус-вектора  значение параметра
значение параметра  согласно сетке
согласно сетке
 : :  . .
| (3)
|
Найдём значения произвольных постоянных векторов в выражении (2) из условий интерполирования кривой 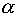 полиномом (2):
полиномом (2):
 . .
| (4)
|
Подставляя (2) в условия (4), получим систему 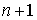 векторных линейных алгебраических уравнений для нахождения постоянных векторов в выражении (2):
векторных линейных алгебраических уравнений для нахождения постоянных векторов в выражении (2):
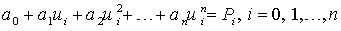 . .
| (5)
|
Эту систему уравнений можно записать в компактной матричной форме:
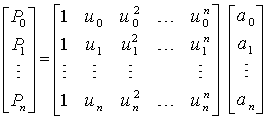 .
.
Система векторных линейных алгебраических уравнений (5) эквивалентна трём системам скалярных алгебраических уравнений относительно проекций радиус-вектора 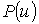 на базисные векторы
на базисные векторы 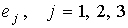 соответственно:
соответственно:
 , ,
|
(6)
|
где 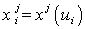 - заданные значения проекций радиус-вектора в точках
- заданные значения проекций радиус-вектора в точках 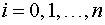 ;
;
 - проекция постоянного вектора
- проекция постоянного вектора 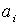 на ось
на ось  системы координат
системы координат  .
.
При этом все системы уравнений (6) будут иметь одинаковые матрицы коэффициентов:
 . .
|
(7)
|
В связи с этой особенностью при интерполировании кривой 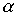 параметрическим полиномом достаточно решить одну систему линейных алгебраических уравнений (6) с тремя правыми частями. При этом каждая правая часть системы будет соответствовать j-ой проекции постоянных радиус-вектора
параметрическим полиномом достаточно решить одну систему линейных алгебраических уравнений (6) с тремя правыми частями. При этом каждая правая часть системы будет соответствовать j-ой проекции постоянных радиус-вектора  на оси координат
на оси координат  .
.
Матрица (7) является матрицей Вандермонда, и её определитель отличен от нуля в силу выбора узлов сетки  согласно (3). Следовательно, система уравнений (6) имеет единственное решение.
согласно (3). Следовательно, система уравнений (6) имеет единственное решение.
На практике для интерполирования значений функции в точках иногда применяют полиномы, предложенные Лагранжем:
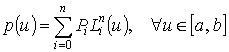 , ,
| (8)
|
где 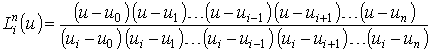 ,
,  ;
;
 - базисные полиномы интерполяции Лагранжа.
- базисные полиномы интерполяции Лагранжа.
В этом случае для построения полинома (8) не нужно решать систему линейных алгебраических уравнений вида (5), полином явно выражается через исходные величины  .
.
Если в точках заданы не только значения радиус-вектора  , но и производные
, но и производные  , то единственным полиномом наименьшей степени, имеющим именно эти значения функции и ее производных во всех точках, является интерполяционный полином Эрмита:
, то единственным полиномом наименьшей степени, имеющим именно эти значения функции и ее производных во всех точках, является интерполяционный полином Эрмита:
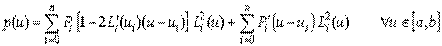 . .
| (9)
|
Так как полином  имеет степень
имеет степень  , то полином Эрмита будет иметь степень
, то полином Эрмита будет иметь степень  . Для конструирования обводов чаще применяют кусочные полиномы Эрмита, определяющие участки между каждой парой точек. Тогда в случае
. Для конструирования обводов чаще применяют кусочные полиномы Эрмита, определяющие участки между каждой парой точек. Тогда в случае  полином интерполирует заданные узловые точки и заданные в них касательные векторы, а в случае
полином интерполирует заданные узловые точки и заданные в них касательные векторы, а в случае 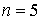 - также векторы вторых производных. Существенным недостатком такой интерполяции является невозможность целенаправленной локальной модификации обвода, так как эта процедура, по существу является подгонкой кривой и зависит от математической подготовки или опыта конструктора.
- также векторы вторых производных. Существенным недостатком такой интерполяции является невозможность целенаправленной локальной модификации обвода, так как эта процедура, по существу является подгонкой кривой и зависит от математической подготовки или опыта конструктора.
Следует отметить, что применение для интерполирования полиномов высоких степеней в большинстве случаев приводит к нежелательным осцилляциям кривых, особенно вблизи крайних узлов промежутка интерполирования. Поэтому полиномы степеней 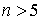 редко применяются при построении численных алгоритмов, использующих интерполирование.
редко применяются при построении численных алгоритмов, использующих интерполирование.
Задачу интерполирования некоторого набора данных параметрическими полиномами можно представить с помощью так называемого приближения Вандермонда. Уравнение (1) запишем в следующем виде:
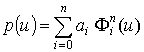 , , 
|
(10)
|
Для определения коэффициентов полинома (10) надо решить три линейных системы уравнений. Запишем обобщенную матрицу Вандермонда:
 ,
,
где 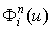 представляет собой базис пространства всех полиномов степени не выше
представляет собой базис пространства всех полиномов степени не выше  .
.
Определитель обобщенной матрицы Вандермонда также отличен от нуля, следовательно, система уравнений для определения коэффициентов полинома (10) имеет единственное решение. Доказано, что для геометрического моделирования гладких кривых и обводов в качестве 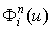 удобно использовать полиномы Бернштейна. Одной из актуальных в этом случае является задача преобразования различных полиномиальных базисов в базис Бернштейна.
удобно использовать полиномы Бернштейна. Одной из актуальных в этом случае является задача преобразования различных полиномиальных базисов в базис Бернштейна.

 с использованием обычных однозначных функций. Кривые инженерных объектов могут иметь вертикальные касательные, что тесно связано с многозначностью функций. Поэтому в автоматизированном проектировании ведущую роль играет параметрическое представление участков кривых.
с использованием обычных однозначных функций. Кривые инженерных объектов могут иметь вертикальные касательные, что тесно связано с многозначностью функций. Поэтому в автоматизированном проектировании ведущую роль играет параметрическое представление участков кривых.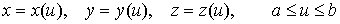 .
. , где
, где  - радиус-вектор точки на кривой;
- радиус-вектор точки на кривой;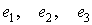 - орты координатных осей;
- орты координатных осей; - параметр точки на кривой.
- параметр точки на кривой.
 -ой степени может быть легко вычислен по схеме Горнера, которая реализуется с помощью
-ой степени может быть легко вычислен по схеме Горнера, которая реализуется с помощью  арифметических действий. Схема Горнера удобна для реализации на компьютере благодаря цикличности вычислений и необходимости сохранять кроме коэффициентов полинома и значений аргумента только одной промежуточной величины. Полином
арифметических действий. Схема Горнера удобна для реализации на компьютере благодаря цикличности вычислений и необходимости сохранять кроме коэффициентов полинома и значений аргумента только одной промежуточной величины. Полином 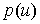 единственным образом разлагается в произведение из
единственным образом разлагается в произведение из 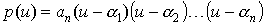 .
.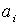 , являющимися вещественными числами. Решения
, являющимися вещественными числами. Решения  вещественного полинома обладают следующими свойствами:
вещественного полинома обладают следующими свойствами: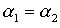 );
); ,
,  ,
,
 - произвольные постоянные векторы;
- произвольные постоянные векторы; - интервал изменения параметра
- интервал изменения параметра 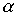 .
.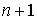 точках кривой
точках кривой 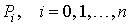 .
. значение параметра
значение параметра  согласно сетке
согласно сетке :
:  .
.
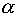 полиномом (2):
полиномом (2): .
.
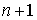 векторных линейных алгебраических уравнений для нахождения постоянных векторов в выражении (2):
векторных линейных алгебраических уравнений для нахождения постоянных векторов в выражении (2):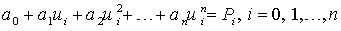 .
.
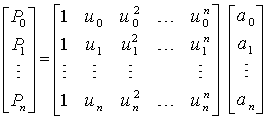 .
.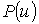 на базисные векторы
на базисные векторы 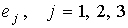 соответственно:
соответственно: ,
,
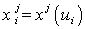 - заданные значения проекций радиус-вектора в точках
- заданные значения проекций радиус-вектора в точках 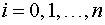 ;
; - проекция постоянного вектора
- проекция постоянного вектора  системы координат
системы координат  .
. .
.
 на оси координат
на оси координат 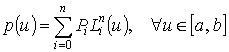 ,
,
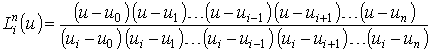 ,
,  ;
; - базисные полиномы интерполяции Лагранжа.
- базисные полиномы интерполяции Лагранжа. .
. , то единственным полиномом наименьшей степени, имеющим именно эти значения функции и ее производных во всех точках, является интерполяционный полином Эрмита:
, то единственным полиномом наименьшей степени, имеющим именно эти значения функции и ее производных во всех точках, является интерполяционный полином Эрмита: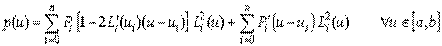 .
.
 имеет степень
имеет степень  . Для конструирования обводов чаще применяют кусочные полиномы Эрмита, определяющие участки между каждой парой точек. Тогда в случае
. Для конструирования обводов чаще применяют кусочные полиномы Эрмита, определяющие участки между каждой парой точек. Тогда в случае  полином интерполирует заданные узловые точки и заданные в них касательные векторы, а в случае
полином интерполирует заданные узловые точки и заданные в них касательные векторы, а в случае 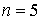 - также векторы вторых производных. Существенным недостатком такой интерполяции является невозможность целенаправленной локальной модификации обвода, так как эта процедура, по существу является подгонкой кривой и зависит от математической подготовки или опыта конструктора.
- также векторы вторых производных. Существенным недостатком такой интерполяции является невозможность целенаправленной локальной модификации обвода, так как эта процедура, по существу является подгонкой кривой и зависит от математической подготовки или опыта конструктора.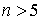 редко применяются при построении численных алгоритмов, использующих интерполирование.
редко применяются при построении численных алгоритмов, использующих интерполирование.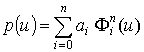 ,
, 
 ,
,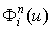 представляет собой базис пространства всех полиномов степени не выше
представляет собой базис пространства всех полиномов степени не выше 


