МЕТОД ТЕНЗОРНОГО ПРОИЗВЕДЕНИЯПо заданному массиву
где
В случае, если все весовые коэффициенты равны между собой, уравнение описывает интегральную поверхность Безье. Параметрические уравнения, определяющие рациональную поверхность Безье, часто записывают в матричной форме [12]:
где
Основные свойства рациональных поверхностей Безье: Поверхность полностью определяется набором вершин характеристической сетки Поверхность лежит в выпуклой оболочке точек Самой поверхности в общем случае принадлежат только четыре угловые точки сетки. В этих точках касательные плоскости поверхности совпадают с плоскостями угловых граней характеристической сетки. Граничными кривыми порции поверхности являются рациональные кривые, управляемые набором точек и соответствующих весов. Рациональная поверхность Безье аффинно- и проективно-инвариантна. Формой поверхности можно управлять подбором вершин характеристической сетки и соответствующих весовых коэффициентов.
|
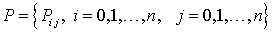рациональная поверхность определяется уравнением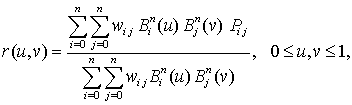
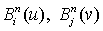- полиномы Бернштейна;
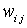- весовые коэффициенты (
).
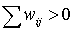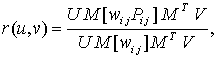
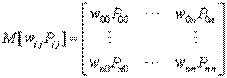- матрица управляющих точек с весами;
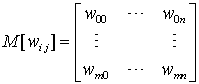- матрица весов;
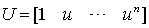- матрица параметра 
;
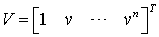- матрица параметра 
;
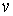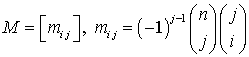- матрица коэффициентов.
.
.
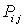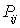