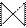 1.1.1. Объектом управления (ОУ) является технологическая операция наполнения резервуара жидкостью. Резервуар (tank), в котором необходимо регулировать уровень L(level), заполняется через регулируемый клапан valve (рис.1.1). valve
    Fin
U tank
L-L0 L L Ta
      1
L0
  2 level L
Fout
Рис.1.1. Управление уровнем воды в резервуаре.
1.1.2. Если с помощью клапана valve управлять потоком жидкости на входе Fin (расход по притоку), то поток на выходе Fout (расход по потреблению) будет зависеть от сечения выходного трубопровода (которое остается постоянным) и давления, зависящего от уровня воды L. Эта зависимость определяется с помощью уравнения Бернулли для сечения 1 - 1, совпадающего с уровнем, и для сечения 2 - 2, проходящего через выходной трубопровод и выходное отверстие резервуара:
L + P1/ρg + (v1)2/2g = P2/ρg + (v2)2/2g,(1.1)
где P1 и P2 –пьезометрические давления в резервуаре и выходном трубопроводе соответственно в Па;
v1 и v2 - скорости движения жидкости в резервуаре и выходном трубопроводе соответственно в м/сек;
ρ – плотность жидкости в кг/м3;
g – ускорение свободного падения, равное 9.81 м/сек2.
Если положить, что v1<< v2 и P1≈ P2, то из уравнения (1.1) следует
 (1.2)
Расход по потреблению будет равен
Fout=V2*πD2/4, (1.3)
где D – диаметр выходного трубопровода.
1.1.3. С учетом (1.2) зависимость (1.3.) носит нелинейный характер, что усложняет аналитическое проектирование автоматической системы стабилизации уровня с использованием, например, ПИД – регуляторов [2],[3]. В них для управления уровнем должны быть определены
1) отклонение error=L0 – L, где L0 – требуемое значение уровня(уставка);
2) скорость изменения этого отклонения rate = d(error) / dt.
Тогда управление U клапаном valve на выходе аналогового ПИД - контроллера определяется в соответствии с выражением
U=Kp*error + Ki* s-1 error +Kd *s error, (1.4.)
где Kp, Ki, Kd – пропорциональная, интегральная и дифференциальная настройки, s – оператор дифференцирования. Основная проблема использования ПИД - контроллеров заключается в определении оптимальных настроек Kp, Ki, Kd, т.е. в решении задачи нелинейного программирования:
на множестве Kp, Ki, Kd при ограничениях в виде равенств 1.1 – 1.4.
1.1.4. Избежать строгого решения этой проблемы можно с помощью нечеткой системы[1], в которой математическая модель системы (1.1 – 1.4) не используется, а процесс управления клапаном описывается набором следующих экспертных правил:
| 
