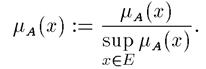Предварительные сведения
2.1.1. Пусть X — универсальное множество, х — элемент X, а К — некоторое свойство. Обычное (четкое) подмножество А универсального множества X, элементы которого удовлетворяют свойству К, определяется как множество упорядоченных пар A = { μA(x) / x } , где μA(x) — характеристическая функция, принимающая значение 1, если х удовлетворяет свойству К, и 0 — в противном случае. Нечеткое подмножество отличается от обычного тем, что для элементов х из X нет однозначного ответа «да-нет» относительно свойства К. В связи с этим нечеткое подмножество А универсального множества X определяется как множество упорядоченных пар A = { μA(x) / x } , где μA(x) — характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве М (например, М = = [0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М = {0, 1}, то нечеткое подмножество А может рассматриваться как обычное или четкое множество. 2.1.2. Пусть М = [0, 1] и А — нечеткое множество с элементами из универсального множества Е и множеством принадлежностей М. • Величина sup μA(x) называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна 1 (sup μA(x) = 1). При sup μA(x) < 1 нечеткое множество называется субнормалъным. • Нечеткое множество пусто, если для любого x из X μA(x) = 0. Непустое субнормальное множество можно нормализовать по формуле
• Нечеткое множество унимодалъно, если μA(x) = 1 только на одном х из Е. • Носителем нечеткого множества А является обычное подмножество со свойством μA(x) > 0, т.е. носителъ А = { х/х из X, μA(x) > 0}. • Элементы х из X, для которых μA(x) = 0,5, называются точками перехода множества А. 2.1.3. Понятия нечеткой и лингвистической переменных используются при описании физических объектов и явлений. Нечеткая переменная характеризуется тройкой (а, X, А), где а — наименование переменной; X — универсальное множество (область определения а); А — нечеткое множество на X, описывающее ограничения, т.е. µa ( x) на значения нечеткой переменной а. Лингвистической переменной (ЛП) называется набор ( ρ, Т, X, С, М), где ρ;— наименование лингвистической переменной; Т — множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X; С — синтаксическая процедура, позволяющая оперировать элементами терм-множества Т, в частности, генерировать новые термы (значения); М — семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой С, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество. 2.1.3.Наиболее часто используются следующие типы функций принадлежности (memberfunction mf): Треугольная: trimf=max(min((x-a)/(b-a),(c-x)/(c-b)),0); Трапецеидальная: trapmf =max(min(min((x-a)/(b-a),1),(d-x)/(d-c)),0); Гаусса: gaussmf=exp(-(x-c)^2/2/σ^2), где a, b, c, d, σ; – параметры.
2.1.4. Нечеткая переменная уровень может быть представлена в виде ρ=’level’, T={‘high’,’okay’,’low’}, X=[ -1 1]. 2.1.5. Нечеткая переменная скорость может быть представлена в виде ρ=’rate’, T = {‘ negative ’,’positive’}, X=[ -0.1 0.1]. 2.1.6. Нечеткая переменная клапан может быть представлена в виде ρ=’valve’, T = {‘no_change’,’open_fast’,’close_fast’,’open_slow’,‘close_slow’}, X=[ -0.1 0.1].
|