Проектирование нечеткого контроллера
2.3.1. Проектирование нечеткого контроллера осуществляется с использованием FIS-Editor. Для этого запустите MatLab, в командном окне наберите fuzzy и нажмите клавишу ENTER. 2.3.2. Появится панель FIS- Editor с именем Untiled: 2.3.3. Создайте fis– файл с именем FazCont, используя File>Export>To File, и приступите к созданию нечетких переменных. Входные переменные имеют тип input, а выходные тип output. Входным переменным присвоим имена level (уровень) и rate (скорость). Выходной переменной присвоим имя valve (клапан). 2.3.4. Иконка input, окрашенная в желтый цвет, обведена красной рамкой. Это означает, что она активна. В окне Name замените слово input1 на слово level и нажмите на клавишу ENTER. Убедитесь, что первая входная переменная получила введенное имя (оно указано под иконкой). 2.3.5. С помощью Edit>Add Variable>Input создайте иконку для второй входной переменной rate аналогично п.2.3.4. Щелкните один раз по иконке выходной переменной output1, появится красная рамка вокруг иконки, в окне Name замените слово output1 на слово valve и нажмите на клавишу ENTER. Исходная панель FIS- редактора с именем FazCont примет вид, представленный на рис.2.1.
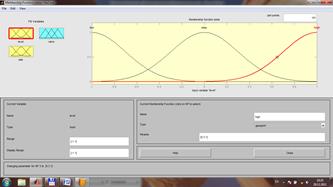
2.3.6. Дважды щелкните ЛК на иконке level. Появится панель В окне Range в квадратных скобках установите диапазон изменения переменной level [ -1 1]. Это означает, что переменная level может принимать значения от -1 до 1 в метрах (между числами пробел и квадратные скобки обязательны!!). Нажмите клавишу ENTER. 2.3.7. В окне Membership Function Plots на прямой mf1 щелкнуть один раз ЛК. Линия окрасится в красный цвет, в окне Name замените слово mf1 на слово high (высокий). В выпадающем окне Type установите тип функции принадлежности gaussmf, а в окне params установите значения 0,3 (среднеквадратическое отклонение) и -1 (среднее значение). 2.3.8. Аналогично п.2.3.7 на прямой mf2 щелкнуть один раз ЛК. Линия окрасится в красный цвет, и в окне Name замените слово mf2 на слово okay (хороший). В выпадающем окне Type установите тип функции принадлежности gaussmf, а в окне params установите значения 0,3 (среднеквадратическое отклонение) и 0 (среднее значение). 2.3.9. Аналогично п.2.3.7 на прямой mf3 щелкнуть один раз ЛК. Линия окрасится в красный цвет, и в окне Name замените слово mf3 на слово low (низкий). В выпадающем окне Type установите тип функции gaussmf, а в окне params установите значения 0,3 (среднеквадратическое отклонение) и 1 (среднеезначение). В результате панель представления переменных примет вид
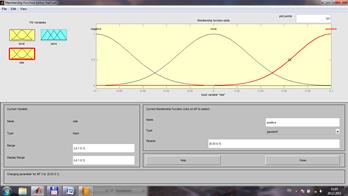
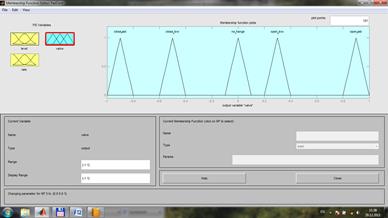
Таким образом, результат нечеткого представления лингвистической переменной level будет иметь следующий вид: Терм1 name: ' high ' type: 'gaussmf' params: [0.3 -1] Терм2 name: 'okay' type: 'gaussmf' params: [0.3 0] Терм3 name: 'low' type: 'gaussmf'l params: [0.3 1] 2.3.10. Аналогично п.п.2.3.6 – 2.3. 9 произведите нечеткое представление переменной rate: Терм1 name: 'negative' type: 'gaussmf' params: [0.03 -0.1] Терм2 name: 'none' type: 'gaussmf' params: [0.03 0] Терм3 name: 'positive' type: 'gaussmf' params: [0.03 0.1] 2.3.11. В результате нечеткого представления переменная rate примет вид: 2.3.12. Аналогично п.п.2.3.6 – 2.3. 9 произведите нечеткое представление выходной переменной valve с диапазоном range: [-1 1]: Терм1 name: 'close_fast' type: 'trimf' params: [-1 -0.9 -0.8] Терм2 name: 'close_slow' type: 'trimf' params: [-0.6 -0.5 -0.4] Терм3 name: 'no_change' type: 'trimf' params: [-0.1 0 0.1] Терм4 name: 'open_slow' type: 'trimf' params: [0.2 0.3 0.4] Терм5 name: 'open_fast' type: 'trimf' params: [0.8 0.9 1] 2.3.13. В результате панель нечеткого представления переменной valve примет вид:
Контрольные вопросы. 1.В чем состоит различие между четкими и нечеткими множествами? 2. Дайте определение функции принадлежности нечеткого множества. 3. Дайте определение лингвистической переменной. 4. Какие типы функции принадлежности Вы знаете? 5. Как использоватьFis-Еditorдля нечеткого представления данных?
|

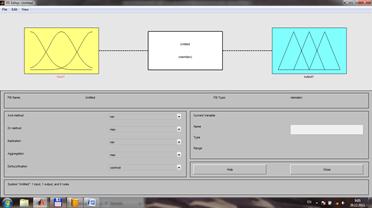
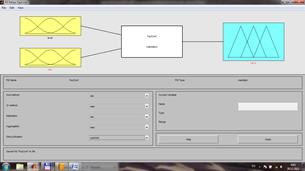 Рис.2.1. Окно FIS – Editor FazCont.
Рис.2.1. Окно FIS – Editor FazCont.