Зіліссіз болғандықтан Осы теңсіздіктен , яғни -теңдеудің түбірі. Сонымен қоса
Бұл әдісті көп жағдайларда, теңдеудің түбірлерінің бастапқы жуық мәнін табуға қолдануға болады. Дісте функцияның туындыларына ешқандай шек қойылмайтын- дықтан және алгоритмі қарапайым болу себепті, әдіс ЭВМ-де теңдеуді шешуге өте қолайлы.
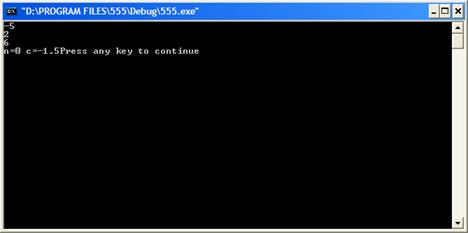
#include <iostream.h>; #include <math.h>; double f(double x) { double s=sin(pow(x,3))-2*x; return s; } void main () { int n=0; double d,a,b,c,h,E; cin >> a >> b >> E; d=(b-a)/2;c=a+d; if(f(a)==0){c=a;cout<<"c="<<c;} if(f(b)==0){c=b;cout<<"c="<<c;} if(f(c)==0){cout<<"c="<<c;} if (f(a)*f(b)>0) {cout<<"duris emes baska san engiz"<<" " << endl;;} else if(f(a)*f(b)<0) { while (fabs(f(c))>E) { d=(b-a)/2;c=a+d; if(f(c)*f(a)>0) {a=c;} if(f(c)*f(b)>0) {b=c;} n++;} cout<<"n="<<n<<" "<<"c="<<c;} }
Ньютон әдісі. (Жанама әдісі) Айталық,
Енді Егер теңдеуінің сол жағын
Сондықтан
Бұл формуланы Ньютон әдісі деп атайды. Енді Ньютон әдісінің жинақтылығын бағалайық. Тэйлор формуласын қолдану арқылы
формуласын аламыз. Мұнда (3.10) формуласынан (3.1) формуласын ескере отырып, мына формуланы аламыз:
Егер
Осыдан Ньютон әдісінің жинақталу жылдамдығы шығады. #include <iostream.h> #include <math.h> double f(double n) { double s=2*pow(n,2)+n; return s; } double g(double n) { double h=6*pow(n,2)+2; return h; }
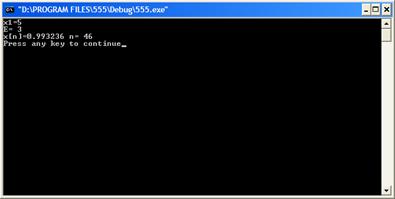
double x[1000000]; int main() { int i=0; double d,x1,e,c; cout<<"x1="; cin >> x1; cout<<"E= "; cin>> e; x[0] = x1; d=f(x1)/g(x1); if (f(x1) == 0) { c=x1; } else { while(fabs(f(c)) > e) { d=f(x[i])/g(x[0]); x[i+1] = x[i] - d; c=x[i+1]; i++; }} cout << "x[n]=" <<c<< " n= " << i << endl; return 0; }
1)x1=4; E=2;x[n]=0.770049; n=36
2)x1=3; E=2; x[n]=0.775729;n=18;
3)x1=5; E=3; x[n]=0.993236;n=46
|

 . (2)
. (2)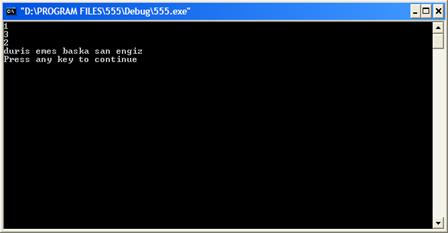
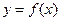 функциясы
функциясы  кесіндісінде төмендегі шарт- тарды қанағаттандырсын:
кесіндісінде төмендегі шарт- тарды қанағаттандырсын:
 функциялары үзіліссіз.
функциялары үзіліссіз.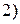
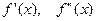 таңбаларын өзгертпейді.
таңбаларын өзгертпейді.
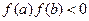 .
.
 болғанда
болғанда 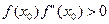 теңсіздігі орындалады.
теңсіздігі орындалады.
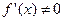 .
.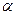 берілген
берілген  теңдеуінің шешуі, ал
теңдеуінің шешуі, ал 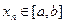 теңдеудің жуық шешуі болса, онда
теңдеудің жуық шешуі болса, онда 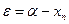 жеткілікті аз шама. Осыдан
жеткілікті аз шама. Осыдан 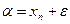 .
.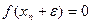 (1)
(1)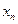 нүктесінде Тэйлор қатарына жіктесек
нүктесінде Тэйлор қатарына жіктесек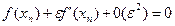 теңдігін аламыз. Осыдан
теңдігін аламыз. Осыдан  өте аз шама десек, онда
өте аз шама десек, онда 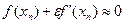 жуықтау теңдігінен
жуықтау теңдігінен  -ды табамыз:
-ды табамыз: , (2)
, (2) . Немесе
. Немесе  деп аламыз. Яғни дәлдігі жоғары келесі жуық шешу былайша табылады:
деп аламыз. Яғни дәлдігі жоғары келесі жуық шешу былайша табылады: . (3.)
. (3.)
 Осыдан
Осыдан  . (3.1)
. (3.1)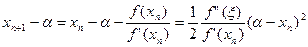 .
.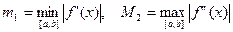 деп белгілесек, онда
деп белгілесек, онда , (3.2)
, (3.2)