Функция және оның графигі
Функция – басқа мәліметтер алу үшін анықталған мәліметтерге қолданылатын компьютердің іс-әрекеті. Функцияның ерекшелігі – оның орындалуы барысында бір ғана нәтиже шығады, ал енгізілген параметрлері бірнешеу болуы мүмкін. Нәтиже функция атауымен белгіленіп, негізгі бағдарламаға беріледі. Функцияның анықталуы: int simple_function () { return 0; } Функция екі жағдайда қолданылады: 1. Егер функция денесіндегі опетаторлар, программада көп кездескенде. Онда, оларға бөлек функция жариялаймыз. Осы жағдайда, программа коды қысқарады. 2. Егер программада, бірнеше операторлар қандай да бір нақты тапсырманы орындаған жағдайда. Осы жағдайда, программа көлемі қысқармауы мүмкін, бірақ программа нақтырақ болады. #include<iostream.h> #include<math.h> #include<fstream.h> void main() {ofstream write_file("mk.dat"); int a,b,n,h; cin >> a >> b >> n; h=(b-a)/n; for(double x=a;x<=b;x+=h) { cout << x << " " <<(cos(x)*sin(x))/(cos(x)-2*cos(x)) << endl;
write_file<< x << " " << (cos(x)*sin(x))/(cos(x)-2*cos(x)) << endl;} } }
2) #include<iostream.h> #include<math.h> #include<fstream.h> void main() {ofstream write_file("mk.dat"); int a,b,n,h; cin >> a >> b >> n; h=(b-a)/n; for(double x=a;x<=b;x+=h) { cout << x << " " <<(pow(x,5)+pow(x,3)-pow(x,2))/(pow(x,6))<< endl;
write_file<< x << " " << (pow(x,5) +pow(x,3)-pow(x,2))/(pow(x,6))<< endl;} }
3) #include<iostream.h> #include<math.h> #include<fstream.h> void main() {ofstream write_file("mk.dat"); int a,b,n,h; cin >> a >> b >> n; h=(b-a)/n; for(double x=a;x<=b;x+=h) { cout << x << " " <<sin(2*x)+cos(x*5)-5<< endl;
write_file<< x << " " << sin(2*x)+cos(x*5)-5<< endl;}}
Тік төртбұрыш әдісі. интегралдыжуықтап былайша есептейміз:
мұндағы Бұл формуланың геометриялық мағынасы мынандай:
АВСД қисық сызықты трапецияның ауданы биіктігі Сондықтан бұл формуланы тік төртбұрыш әдісі дейді. (1.1) формуласының дәлдігі
Тейлор формуласы арқылы оңай табылады. Шынында да
және
формуласын аламыз. Егер М
Яғни болғандықтан, h Енді (1.1) теңдіктің i-дің 1 ден N ге дейінгі қосындысын қарастырсақ
болады. Сондықтан Осыдан
Егер
яғни тік төртбұрыш әдісінің
С++ тілінде есепті жүзеге асыру программасы:
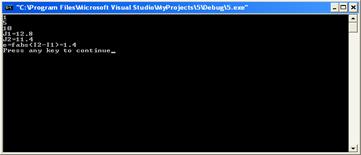
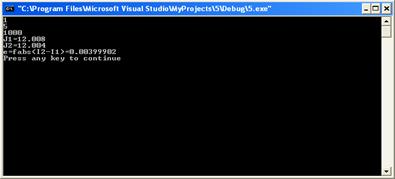
#include <iostream.h> #include <math.h> double f(double x) { return x; } void main() { double a,b,s,x[100],J1,J2,h,h1; float e,s1,s2; int n; cin >> a >>b >>n; h=(b-a)/n; h1=(b-a)/(2*n); s1=0;s2=0; for(double i=a+h; i<=b; i+=h) {s1+=f(i);} J1=s1*h; cout<<"J1="<<J1<<endl; for(i=a+h1; i<=b; i+=h1) {s2+=f(i);} J2=s2*h1; cout<<"J2="<<J2<<endl; e=fabs(J2-J1); cout<<"e=fabs(I2-I1)="<<e<<endl;}
1) a=1;b=5;n=10
2) a=1;b=5;n=100
3)a=1;b=5;n=1000
|







 (1.1)
(1.1)
 2-сурет
2-сурет АВД/C/ тік төртбұрышының ауданымен алмастырылады (2-сурет).
АВД/C/ тік төртбұрышының ауданымен алмастырылады (2-сурет). . (1.2)
. (1.2)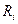 ді былайша жазып
ді былайша жазып =
= 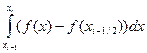 (1.3)
(1.3) +
+ 



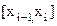
 десек, онда (1.3) формуласынан
десек, онда (1.3) формуласынан  (1.4)
(1.4) =
= 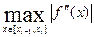 деп R
деп R 
 (1.5)
(1.5) 0 ұмтылғандағы дәлдік 0(h
0 ұмтылғандағы дәлдік 0(h  ) болады.
) болады. (1.6)
(1.6) .
. .
. десек, онда
десек, онда , (1.7)
, (1.7)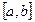 кесіндісіндегі дәлдігі-0(h
кесіндісіндегі дәлдігі-0(h  ).
).