Парабола әдісі. (Симпсон формуласы).
интегралды жуықтап есептеу үшін
Осыдан
Сонымен мына формуланы –
Симпсон немесе парабола формуласы деп атайды. Бұл формуланың парабола формуласы деп атайтын себебі
Симпсон формуласы
Бөлшекті индекстерден құтылу үшін
4-сурет О х у xi-1 xi-1/2 xi y=f(x) y=L2(x) + - Симпсон формуласының жіберетін қатесін қарастырардың алдында, оның үш
Осыдан
Екіншіден
екенін ескерсек
формуласын аламыз. Сонымен Симпсон формуласының үшінші дәрежеге дейінгі кез келген көпмүшелер үшін дәл екенін көрдік. Енді Симпсон формуласының қатесін қарастыру үшін мына шарттарды қанағаттандыратын
интерполяциялық Эрмит көпмүшелігін пайдаланамыз. Симпсон формуласы кез келген үш дәрежелі көпмүшеліктер үшін дәл болғандықтан
Енді десек,онда
мұндағы
-Эрмит көпмүшесінің жіберетін қатесі.
Сондықтан Симпсон формуласының жіберетін қатесi
Hемесе
Симпсон формуласының
Болғандықтан
Яғни Симпсон әдісінің
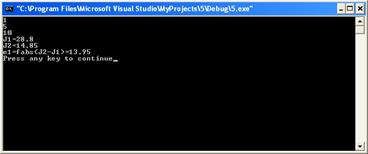
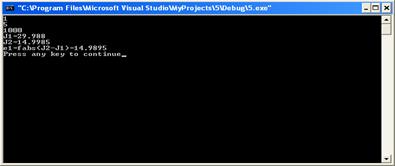
С++ тілінде есепті жүзеге асыру программасы: #include <iostream.h> #include <math.h> double f(double x) { return x; }void main() { double a,b,s,s1,s2,J1,J2,e1,e2,e3; float h,h1,h2,k; int n; double c,c1,c2; cin >> a>> b >> n; s=0;c=0;c1=0;s1=0; h=(b-a)/(2*n); h1=(b-a)/(4*n); k=f(a)+f(b); for(double i=a+h; i<b; i+=2*h) {c+=f(i);} for (i=a+2*h; i<b; i+=2*h) { s+=f(i);} J1=(k+4*c+6*s)*h/2; cout<<"J1="<<J1<<endl; for(i=a+h1; i<b; i+=2*h1) {c1+=f(i);} for (i=a+2*h1; i<b; i+=2*h1) { s1+=f(i);} J2=(k+2*c1+3*s1)*h1/2; cout<<"J2="<<J2<<endl; e1=fabs(J2-J1); cout<<"e1=fabs(J2-J1)="<<e1<<endl; } 1)a=1;b=5n=10
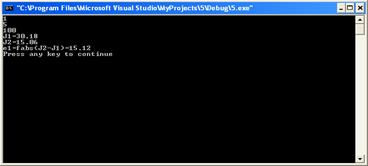
2)a=1;b=5;n=100
3)a=1;b=5;n=1000
Интеграл есептеудің Тіктөртбұрыш,Трапеция,Симпсон әдістеріне анализ Интеграл есептеудің тіктөртбұрыш, трапеция, симпсон әдістеріне анализ жасайық.Берілген 3 функцияны қарастырайық. 1)√х5+х2 ; 2)1/х+2 х5 ; 3)е2х+ х2; Функцияларды берілген [a,b] аралығында салыстырамыз.
1)a=1 b=5
2)a=1; b=5
3)a=1; b=5
Бұдан көретініміз, n өскен сайын интеграл мәні нақтырақ болады. Кестеге қарасақ Симпсон әдісі тиімді, және дәл.Интегралдарды жуықтап есептеу әдісі күрделі есептерді есептеуде кең қолданылады
Қақ бөлу әдісі. (биссекция әдісі) Айталық, теңдеуі берілсін және сонымен қоса
|

 функциясын
функциясын  нүктелері арқылы тұрғызылған
нүктелері арқылы тұрғызылған 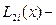 Лагранж көп мүшесімен алмастырамыз. Яғни
Лагранж көп мүшесімен алмастырамыз. Яғни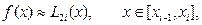
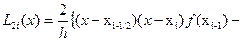
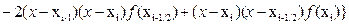 . (1)
. (1)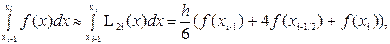
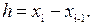

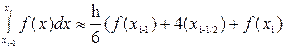 (1.1)
(1.1)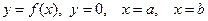 сызықтарымен шектелген қисық сызықты трапецияның ауданы
сызықтарымен шектелген қисық сызықты трапецияның ауданы 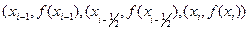 нүктелері арқылы өтетін парабола және
нүктелері арқылы өтетін парабола және 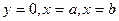 түзулерімен шектелген трапецияның ауданымен алмастырылады (4-сурет).
түзулерімен шектелген трапецияның ауданымен алмастырылады (4-сурет). кесіндісінде былайша жазылады
кесіндісінде былайша жазылады 
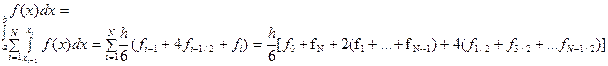

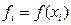
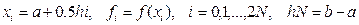 десек,онда Симпсон формуласын былайша жазамыз:
десек,онда Симпсон формуласын былайша жазамыз: 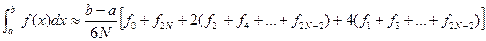 . (1.3)
. (1.3)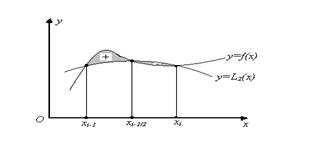
 дәрежелі көпмүше үшін дәл екенін көрсетейік. Шынында да
дәрежелі көпмүше үшін дәл екенін көрсетейік. Шынында да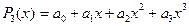 болса, онда
болса, онда
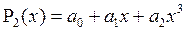
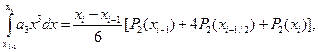

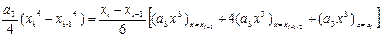

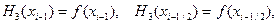
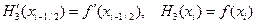
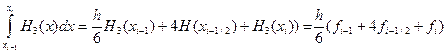 (1.4)
(1.4)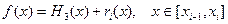
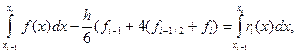
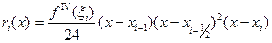 (1.5)
(1.5)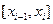 кесіндісінде
кесіндісінде 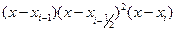 көпмүшесі өзінің таңбасын өзгертпейтін болғандықтан
көпмүшесі өзінің таңбасын өзгертпейтін болғандықтан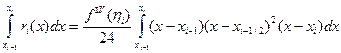
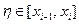
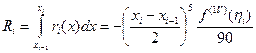 . (1.6)
. (1.6)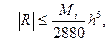 (1.7)
(1.7)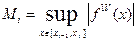
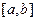 кесіндісінде жіберетін қатесі
кесіндісінде жіберетін қатесі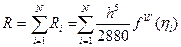
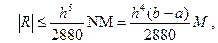 (1.8)
(1.8)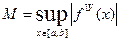
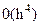 .
. 
 (1)
(1)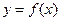 функциясы
функциясы  кесіндісінде үзіліссіз және
кесіндісінде үзіліссіз және 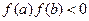 болсын. Теңдеудің алдын ала
болсын. Теңдеудің алдын ала  дәлдікпен берілген түбірін табу үшін
дәлдікпен берілген түбірін табу үшін 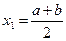 . Егер
. Егер 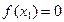 болса, онда теңдеудің шешуін тапқанымыз, ал олай болмаған жағдайда
болса, онда теңдеудің шешуін тапқанымыз, ал олай болмаған жағдайда  немесе
немесе 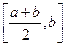 кесінділерін қарастырамыз, егер
кесінділерін қарастырамыз, егер 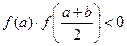 болса, онда
болса, онда 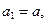
 деп аламыз, олай болмаса
деп аламыз, олай болмаса 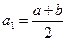 ,
, 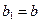 деп аламыз. Осыдан кейін
деп аламыз. Осыдан кейін  кесіндісін қақ бөлу арқылы
кесіндісін қақ бөлу арқылы 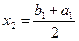 табамыз. Егер
табамыз. Егер 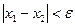 болса, онда теңдеуді жуық түбірі табылды деп есептейміз, ал олай болмаған жағдайда
болса, онда теңдеуді жуық түбірі табылды деп есептейміз, ал олай болмаған жағдайда  кесіндісін тағы қақ бөлеміз. Осы процестерді қайталау арқылы
кесіндісін тағы қақ бөлеміз. Осы процестерді қайталау арқылы 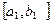 ,
, 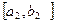 ,…,
,…, 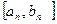 кесінділер тізбегін аламыз. Бұл кесіндіде
кесінділер тізбегін аламыз. Бұл кесіндіде 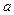
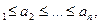
 болғандықтан және
болғандықтан және 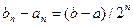 теңдігі орындалатындықтан
теңдігі орындалатындықтан 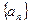
 тізбектерінің ортақ шегі бар, яғни
тізбектерінің ортақ шегі бар, яғни