Трапеция әдісі.
бір дәрежелі Лагранж көпмүшесімен алмастырсақ, онда
мұндағы (1.8) формуласын
теңдігін аламыз. Осыдан
3-сурет
(1.9) формуладан бұл әдістің жіберетін қатесі
екенін көреміз. Ал жоғарыдан бағаласақ
Енді интегралды былай есептесек:
Онда
трапеция әдісінің жалпы формуласы шығады. Ал жіберілетін қате
Жоғарыдан бағаласақ
Сонымен, трапеция әдісінің
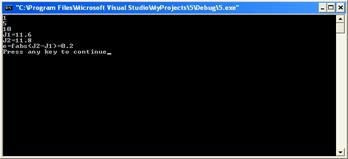
#include <iostream.h> #include <math.h> double f(double x) { double s=x; return s; } void main() {double a,b,s,s1,J1,J2,x[100]; float h,h1,c,e; int n; cin >>a >>b >>n; s=0; s1=0; h=(b-a)/n; h1=(b-a)/(2*n); c=(f(b)-f(a))/2; for(double i=a+h; i<b; i+=h) { s+=f(i);} J1=(c+s)*h; cout<<"J1="<<J1<<endl; for(double j=a+h/2; j<b; j+=h/2) { s1+=f(j);} J2=(c+s1)*h/2; cout<<"J2="<<J2<<endl; e=fabs(J2-J1); cout<<"e=fabs(J2-J1)="<<e<<endl;}
1) a=1;b=5;n=10
2) a=1;b=5;n=100
3) a=1;b=5;n=1000
|

 функциясын
функциясын 
 нүктелері арқылы тұрғызылған
нүктелері арқылы тұрғызылған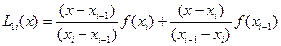
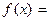
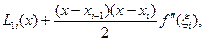 (1.8)
(1.8)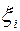
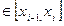
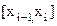 аралығында интегралдау арқылы
аралығында интегралдау арқылы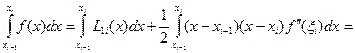
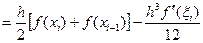 (1.9)
(1.9)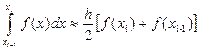 . Бұл формула трапеция әдісі деп аталады,себебі
. Бұл формула трапеция әдісі деп аталады,себебі 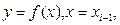

 сызықтарымен қоршалған қисық сызықты трапецияның ауданы
сызықтарымен қоршалған қисық сызықты трапецияның ауданы  трапециясының ауданымен алмастырылады (3сурет).
трапециясының ауданымен алмастырылады (3сурет). (2)
(2)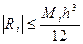 ,
,


 (2.1)
(2.1)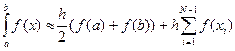 (2.2)
(2.2) (2.3)
(2.3) , (2.4)
, (2.4) .
. кесіндісіндегі дәлдігі
кесіндісіндегі дәлдігі 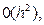 екенін көреміз.
екенін көреміз.