Приклади. Приклад 1. Розв'язати нерівність: 0,41о§2 х+1 < 6,252-1о§2 х'.
Приклад 1. Розв'язати нерівність: 0,41о§2 х+1 < 6,252-1о§2 х'.
Оскільки основа ступеня 0 < — < 1, то при переході до нерівності, що має показники ступеня, знак нерівності змінюється: log2 X +1 > 2log2 X3 - 4. Функція log2 x визначена при x > 0, тому, за властивістю логарифму k 3 log ax = k ■ log ax, маємо: 2log2 x = 6log2 x. Перенесемо всі доданки з правої частини рівняння в ліву. Одержимо нерівність: log2 x - 6log2 x + 5 > 0. Робимо заміну У = Іо§2 х, приходимо до нерівності: " 3 ±>/9-5 = 3 ± 2. Методом інтервалів знаходимо змінну у: У < 1 і У > 5. Таким чином, вихідна нерівність, з урахуванням ОДЗ, рівносильна сукупності нерівностей: Іо§2 х < 1
Іо§2 х > 5
0 < х < 2 Оскільки основа логарифма більше одиниці, то: Відповідь: (0;2)и(32;
Приклад 2. Знайти область визначення функції: У = УІ 1 - іо& ((- 4х + 3). А Оскільки логарифмічна функція визначена тільки для додатних чисел, а квадратний корінь - для невід'ємних чисел, то дана задача зводиться до розв'язку системи нерівностей: х2 - 4х + 3 > 0, 1 -Іо§8(х2 -4х + 3)>0. Ліву частину першої нерівності розкладемо на множники 12 = 2 ± V 4 - 3 = 2 ± 1, а в другій нерівності замінимо 1 на Іо§8 8: (х - 3)(х -1)> 0, 1о§8 (х2 - 4х + 3)< ^8. Оскільки основа логарифма 8 > 1, то, відповідно до властивостей логарифма, переходимо до системи: '(х - 3)(х -1)> 0 або |(х - 3)(х -1)> 0, х2 - 4х + 3 < 8. І х2 - 4х - 5 < 0. Ліву частину другої нерівності розкладемо на множники:
(х - 3)(х -1)> 0, = 2 ±7 4 + 5 = 2 ± 3 (х - 5)(х +1)< 0. Остання система рівносильна нерівності: (х - 3)(х - 1)(х - 5)(х +1)< 0, (при х Ф 3 і х Ф1). Методом інтервалів одержуємо: [-1;1)и(3;5 ].
Відповідь: [-1;1)и(3;5 ].► Приклад 3. Розв'язати нерівність:
log27 J2,5 -6 - log6 325 + 0,6 < 0
Л Знайдемо ОДЗ: 2,5 - x > 0 б ^
— + 0,6 > 0 25
За властивістю логарифму log mb = — • log b = log tfb; log tfb = log mb. m
Маємо: log27 ^2,5 - 6 = log33 22,5 - 6 = log36
log9 І25+0'6=log32 325+0'6=log36
Тоді вихідну нерівність можна переписати у вигляді:
< log* ^ + 0,6 336 25
що еквівалентно (у силу парності показника ступеня) нерівності:
x log36 V 2?+°,6
Остання нерівність, за властивостями модуля, еквівалентна об'єднанню чотирьох систем нерівностей. Потенціюємо, враховуючи, що 36 > 1.
x log6 2,5 -6 V x log,б — + 0,6
V / x log36 2,5 -т < log36
3 V 6 у 3 2,5 - x > 1 б — + 0,6 > 1 25
_ _ x _ x Л, 2,5 — < — + 0,6 б 25 ґ хл 2,5 - - іоб
- іое 2,5 <- іо§ х 2,5 — < 1 6 — + 0,6 < 1 25 2,5 - х > — + 0,6 6 25
;5/ ^ 9 2 /31 Розв'язком другої системи буде
х 9;2853і
х іоел — + 0,6
15 - х < 6 х +15 > 25 2,5 х 3 х > 9 х > 10 (х - 5>/3)(х + 5>/3)< 0
573 - 8,67. Розв'язків немає.
x < 9 x < 10
(x - зТз)(x + зТз)> 0 Розв'язком четвертої системи буде х-5л/3] u[^л/3; 9.
Поєднуючи всі розв'язки, з урахуванням ОДЗ, одержуємо відповідь: -із;J u зл/з;2^ 31. Приклад 4. Розв'язати нерівність log2-x (х + 2)• logх+3 (3 - х)< 0. А Основна ідея розв'язування подібних нерівностей: (l0g aU (Х)- l0g aV (Х))• Р (Х)< 0 ^ \u (х)-v (х))• p (х)< 0 u (х)> 0. v (х)> 0 - перехід до основи а > 1; - заміна різниці логарифмів різницею відповідних функцій при природних обмеженнях на кожну з них; - якщо ліва частина нерівності містить у якості співмножника будь-який логарифм (а не різницю двох логарифмів), то для того, щоб застосувати пропоноване перетворення, необхідно представити цей логарифм у вигляді різниці, віднявши від нього нуль, записаний як логарифм одиниці при тій же основі. l0g2-х (х + 2)• l0gх+3 (3 - х)< 0 ^
Переходимо до основи a = 2. log2 (х + 2) ^ log2 (3 - х) < 0 ^ log2 (х + 2)- log21 ^ l0g2 (3 - х)- l0g21 <0 log2 (2-х) log2 (х + 3) log2 (2-х)-log21 log2 (х + 3)- log2 1 Застосовуємо нрононоване неретворення: ' (X + 2)-1 (3 - x)-1 < 0 Г(+]) (-х) < 0 (2-x)-1 (x + 3)-1 (1 -x) (x + 2) x + 2 > 0 ^ x >-2 3 - x > 0 x < 3 Остання система легко вирішується методом інтервалів. З Щ^І г Відповідь: jcg(-2;-1]U(1;2]> Рис. 1.25. Розв'язок нерівності методом інтервалів Для обчислення натурального логарифма в Maxima використовується функція log. Maxima не має убудованої функції для десятичного логарифма або для інших нідстав. Для нереходу від однієї нідстави логарифма до нідстави натурального логарифма використовуємо формулу logbX = l0g aX =. А для log ab ln b об'єднання логарифмів за формулами logaxk = к • logax і logaxy = logax + logay використовується вбудована функція logcontract. l.S. Індивідуальне завдання № 1.4 Студент новинен розв'язати одну з наведених нижче задач, вибравши її за своїм номером у журналі груни. Розв'язати нерівність: 1. log2x + log2(x +1)<log2(2x + б); 2. log3(x2 -5x + б)<0; 3. log у (log4 (x x - 5)) > 0; 4. logx — > 1; /3 Xx +1
сі 4 х + 5 5. log 1; ши шукані величини через відомі величини і введені змінні. Друга трудність - складання рівнянь і нерівностей, що пов'язують дані величини і змінні. Третя трудність - розв'язування отриманої системи рівнянь або нерівностей бажано найбільш раціональним способом. Скласти рівняння - виразити в математичній формі зв'язок між даними (відомими) і шуканими (невідомими) величинами. Іноді цей зв'язок настільки явно випливає з формулювання завдання, що складання рівняння є просто дослівним переказом завдання мовою математичних знаків. Частіше, однак, трапляється, що зв'язок між даними і шуканими величинами не вказується в завданні прямо; його потрібно встановити, виходячи з умов завдання. У практичних задачах так буває майже завжди. Тому для складання рівняння не можна дати цілком вичерпних вказівок. Таким чином, для розв' язування текстового завдання ми перекладаємо його на математичну мову, тобто створюємо математичну модель. Оволодіння навичками математичного моделювання - це найважливіше, що необхідно для складання рівнянь. Адже, як узагалі відбувається переклад з однієї мови на іншу? Ви читаєте текст і відразу викладаєте його іншою мовою. Саме так перекладає досвідчений фахівець легкі текстові завдання на мову математики. Він відразу бачить що саме прийняти за невідомі величини, яким буде рівняння. Якщо ж зустрілося нелегке завдання, то для перекладу на математичну мову потрібно користуватися наступним. Приймемо за значення шуканої величини (або декількох величин) деяке навмання взяте число (або кілька чисел) і поставимо собі завдання перевірити, чи угадали ми правильний розв'язок завдання чи ні. Якщо ми зуміли провести цю перевірку і знайти, що наша здогадка вірна, або невірна, то ми негайно можемо скласти потрібне рівняння (кілька рівнянь). Отже, запишемо ті самі дії, що ми робили для перевірки, тільки замість навмання взятого числа введемо літеру для невідомої величини. Ми одержимо необхідне рівняння. Перевірку навмання узятого розв'язку можна робити різними способами; відповідно до цього можна одержати для одного й того ж завдання різні види рівняння; всі вони, однак, дадуть для шуканої величини той самий розв'язок; такі рівняння називаються рівносильними одне до одного. Зрозуміло, що після одержання навичок у складанні рівнянь немає потреби робити перевірку навмання взятого числа: можна для визначення шуканої величини брати не число, а деяку літеру (х, у тощо) і поводитись так, ніби ця літера (невідома) була тим числом, яке ми збираємося перевірити.
|


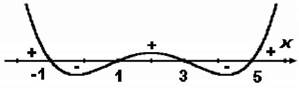

 Рис. 1.22. Область дозволених значень у другому випадку
Рис. 1.22. Область дозволених значень у другому випадку
 Рис. 1.23. Область дозволених значень у третьому випадку
Рис. 1.23. Область дозволених значень у третьому випадку
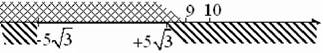 Рис. 1.24. Область дозволених значень у четвертому випадку
Рис. 1.24. Область дозволених значень у четвертому випадку




