Приклади
ЗМІСТ Розділи Стор. ВСТУП........................................................................................................................................ 5 1. Елементарна математика.................................................................................................... 9 1.1. Тригонометрія......................................................................................................... 9 1.2. Індивідуальне завдання № 1.1........................................................................... 20 1.3. Планіметрія.................................................................................................... 21 1.4. Індивідуальне завдання № 1.2........................................................................... 24 1.5. Алгебраїчні рівняння й нерівності................................................................... 26 1.6. Індивідуальне завдання № 1.3................................................................... 34 1.7. Логарифмічні рівняння й нерівності....................................................... 36 1.8. Індивідуальне завдання № 1.4........................................................................... 41 1.9. Складання рівнянь................................................................................................ 42 Контрольні запитання................................................................................................... 46 2. Лінійна алгебра.......................................................................................................... 47 2.1. Визначення матриці............................................................................................. 47 2.2. Види матриць................................................................................................. 48 2.3. Операції над матрицями та їхні основні властивості........................... 48 2.4. Індивідуальне завдання № 2.1........................................................................... 57 2.5. Поняття визначника. Методи обчислення визначників........................ 59 2.6. Властивості визначників............................................................................. 61 2.7. Мінори й алгебраїчні доповнення. Розкладання визначників за елементами рядків і стовпців................................................................................ 62 2.8. Індивідуальне завдання № 2.2........................................................................... 65 2.9. Зворотна матриця......................................................................................... 67 2.10. Індивідуальне завдання № 2.3........................................................................ 70 2.11. Системи лінійних алгебраїчних рівнянь (СЛАР)....................................... 72 2.12. Правило Крамера для розв'язування СЛАР................................................. 73 2.13. Розв'язування СЛАР за допомогою зворотної матриці..................... 76 2.14. Індивідуальне завдання № 2.4........................................................................ 79 2.15. Поняття і знаходження рангу матриці................................................... 81 2.16. Умови існування розв'язку СЛАР загального виду. Теореми Кронекера-Капеллі........................................................................................................................ 84 2.17. Індивідуальне завдання № 2.5........................................................................ 87 2.18. Однорідна система рівнянь. Фундаментальна система. Загальний розв'язок системи................................................................................................................... 90 2.19. Структура розв'язків неоднорідної системи лінійних рівнянь 92 2.20. Розв' язування систем лінійних алгебраїчних рівнянь методом Гаусса 92 2.21. Індивідуальне завдання № 2.6...................................................................... 106 2.22. Індивідуальне завдання № 2.7...................................................................... 107 Контрольні запитання................................................................................................... 109 3. Векторна алгебра............................................................................................................................. 110 3.1. Поняття вектора............................................................................................. 110 3.2. Колінеарні й компланарні вектори................................................................. 110 3.3. Лінійні операції над векторами....................................................................... 111 3.4. Кут між векторами. Проекція вектора на вісь........................................ 114 3.5. Лінійна залежність й незалежність векторів. Векторні лінійні простори 116 3.6. Базис, розкладання вектора за базисом. Ортогональні системи векторів. Перехід від одного базису до іншого........................................................................................... 117 3.7. Декартова система координат.......................................................................... 118 3.8. Напрямні косинуси вектора........................................................................ 120 3.9. Лінійні операції над векторами в координатній формі........................ 121 3.10. Знаходження координат вектора................................................................... 122 3.11. Індивідуальне завдання № 3.1................................................................. 123 3.12. Індивідуальне завдання № 3.2................................................................. 124 3.13. Скалярний добуток векторів і його властивості........................................ 126 3.14. Довжина вектора. Кут між векторами. Умова ортогональ- ності двох векторів 127 3.15. Індивідуальне завдання № 3.3................................................................. 129 3.16. Векторний добуток векторів і його властивості.................................. 130 3.17. Індивідуальне завдання № 3.4................................................................. 134 3.18. Мішаний добуток векторів і його властивості.................................... 135 3.19. Індивідуальне завдання № 3.5........................................................................ 137 3.20. Висота тетраедра (піраміди).......................................................................... 138 3.21. Індивідуальне завдання № 3.6........................................................................ 140 3.22. Поняття власних чисел і власних векторів матриці.................................. 142 3.23. Методи знаходження власних чисел і власних векторів матриці......... 142 3.24. Лінійна модель обміну (модель міжнародної торгівлі).......................... 145 3.25. Індивідуальне завдання № 3.7........................................................................ 147 3.26. Поняття квадратичної матриці й квадратичної форми...................... 148 3.27. Канонічний вигляд квадратичної форми............................................... 150 3.28. Зведення квадратичної форми до канонічного вигляду.......................... 150 3.29. Індивідуальне завдання № 3.8................................................................. 153 3.30. Визначеність квадратичних форм........................................................... 154 3.31. Індивідуальне завдання № 3.9................................................................. 158 Контрольні запитання................................................................................................... 159 ВИСНОВКИ..................................................................................................................... 160 СПИСОК РЕКОМЕНДОВАНОЇ ТА ВИКОРИСТАНОЇ ЛІТЕРАТУРИ.. 161 ПРЕДМЕТНИЙ ПОКАЖЧИК............................................................................................. 162 ДОДАТКИ.............................................................................................................................. 163 ВСТУП Вибравши для себе спеціальність, пов'язану з економікою, студент назавжди зв'язав свою долю з математикою. У стінах вищого навчального закладу студентові доведеться мати справу з безліччю математичних дисциплін, перша з яких «Математика для економістів». Шкільний курс алгебри та геометрії створив фундамент математичної підготовки студента. Необхідно систематизувати, закріпити й протестувати ці знання. Для цього потрібно розв'язати деякі типові задачі з елементарної математики, згадати деякі формули. У цьому плані перший розділ посібника «Елементарна математика» буде настільною книгою для першокурсників. До того ж, наприкінці посібника розміщені витяг із таблиці Брадіса (додаток А) та степені деяких цілих чисел (додаток Б). Відомо, що в основі «Математики для економістів» знаходяться найпростіші, азбучні її положення, що вивчаються в школі. Таким чином, шлях до пізнання сучасної, величезної, майже безмежної за своїм багатством галузі знань, лежить через вивчення елементарної математики. Для розв'язання будь-якої складної задачі, необхідно провести ряд розрахунків, що без допомоги елементарної математики виконати було б неможливо. Основною особливістю всіх математичних наук є їх відвернений або абстрактний характер. Але дійсність завжди конкретна, і тому математичні положення, як і будь-яка теорія, відбивають її лише з деяким наближенням. Ті величини, з якими ми маємо справу при вивченні економіки, є величинами, що змінюються або змінними. «Математика для економістів», вивчає змінні величини не ізольовано, а в їхньому взаємному зв'язку. Бурхливий розвиток сучасної математики тісно пов' язаний із тим, що теорія й практика висувають нові й нові задачі, які математика повинна вирішувати. Старих (елементарних) знань стає недостатньо, доводиться винаходити нові шляхи, нові методи. Так виникла лінійна алгебра, найбільш важлива в застосуваннях частина алгебри. Першим, за часом виникнення, питанням, що відноситься до лінійної алгебри була теорія лінійних рівнянь. Розвиток останньої призвів до створення теорії визначників, а пізніше - теорії матриць і пов'язаної з нею теорії векторних просторів і лінійних перетворень у них, а також теорії квадратичних форм. Ці теорії широко застосовуються в економіці. У цьому посібнику представлені приклади, які наочно показують зв'язок економіки й математики. Крім того, у посібнику запропоновані приклади розв'язування задач із використанням програми Maxima вільного програмного забезпечення. Maxima - це єдина з відкритих програм, здатна посперечатися за можливостями з комерційними Mathematica і Maple, що перевалюють ціною однієї копії за тисячу американських доларів. Для роботи з даною програмою в операційній системі Linux треба в командному рядку набрати команду maxima (xmaxima якщо є графічна оболонка) або нажати мишкою на ярлик робочого стола. У будь-якому випадку при старті виводиться деяка інформація про систему й «мітка» (%i1), що показує готовність програми до уведення команд користувача. Кожне уведення й виведення позначаються програмою й потім можуть бути використані знову. Символ %i (від input) використовується для позначення команд, уведених користувачем, а %o (від output) - при виведення результатів обчислень. Для ініціалізації процесу обчислень необхідно ввести команду, потім символ «;» (крапка з комою) і нажати клавішу Enter. Якщо не потрібно виведення отриманої інформації на екран, то замість крапки з комою використовується символ $. Для арифметичних дій можна використовувати традиційні позначення: «+», «-», «*», «/» і «**» або «л» для піднесення в ступінь. Наприклад, в осередок %i1 можна записати: (%i1) (1/2+1/3+1/4)/(1/5+1/6+1/8); (%o1) 130/59 Як видно з останнього приклада Maxima завжди показує результат у точній аналітичній формі. Якщо потрібно одержати результат обчислення у вигляді числа із плаваючою крапкою, то після виразу, що вводиться наприкінці, треба через кому задати дескриптор numer. Для цих же цілей можна використовувати команду float, що перетворить отриманий результат у потрібний вид: (%i2) float(%o1); (%o2) 2.203389830508475 Звернутися до результату останньої команди можна за допомогою символу %: (%i3) %-12/59; (%o3) 2.0 У цьому випадку %-12/59 - це те ж саме, що й %o2-12/5 9. Це позначення дозволяє звертатися до останнього результату, не відволікаючись на те, який його номер. Для повтору раніше уведеної команди, скажемо (%i3), в операційній системі Linux досить набрати комбінацію Alt + P, а в Windows досить нажати стрілку нагору. Maxima не звертає увагу на регістр уведених символів в іменах убудованих констант і функцій. Запис sin(x) еквівалентний запису SIN(x). Регістр букв, однак, важливий при використанні змінних, наприклад, Maxima уважає x і X різними змінними. Для стандартних математичних констант використовуються наступні позначення: %e - для підстави натуральних логарифмів, %i - для мнимої одиниці (квадратний корінь із числа -1), %pi - для числа п. Позначення для деяких функцій: sqrt - для кореня квадратного, log - для натуральних логарифмів. Для деяких тригонометричних функцій: sin - синус, asin - арксинус, cos - косинус, acos - арккосинус, tan - тангенс, atan - арктангенс. Наприклад, щоб увести sin(n/6), необхідно набрати: sin(%pi/6). Присвоювання значення будь-якої змінної здійснюється за допомогою знака «:» (двокрапка). (%i4) x:2; (%o4) 2 (%i5) y:3; (%o5) 3 (%i6) x + y; (%o6) 5 Символ «=» (дорівнює) використовується при введенні рівнянь або підстановок. Наприклад: (%i7) equation:t^3-t=0; (%o7) t*3-t=0 (%i8) solve(equation,t); (%o8) [t=-1,t=1,t=0] В останньому прикладі ми скористалися убудованою функцією - solve. Таких убудованих функцій в Maxima дуже багато, через них реалізовано майже все, що сприймається як дії над будь-якими об'єктами. Так, у цьому випадку об'єкт - це рівняння, а дія - пошук розв'язку цього рівняння. Такими функціями є, наприклад: linsolve - розв'язування системи лінійних алгебраїчних рівнянь, де число рівнянь дорівнює числу невідомих; algsys, що розв'язує одномірні багаточлени або поліномні рівняння й допускає більшу кількість рівнянь чим змінних або навпаки. У міру вивчення розділів «Математики для економістів» будуть розкриватися всі необхідні функції програми Maxima. Так, наприклад, для розділу «Елементарна математика» будуть корисні функції expand, що розкриває дужки й призводить вираз до канонічного виду; divide, яку можна використовувати для знаходження частки й решти від ділення одного багаточлена на іншій; gcd, що визначає найбільший загальний дільник багаточленів; factor, що здійснює розкладання багаточлена на множники; ratsimp виносить за дужки найбільший загальний дільник. Для завдання додаткових умов використовується функція assume. Функція forget (to forget - забувати) знімає всі обмеження, накладені за допомогою assume. Будь-яке ім'я, що має значення, чи то ім'я осередку %i або %o, чи то будь-яке інше ім'я, що призначено виразу за допомогою «:», можна очистити за допомогою функції kill. Цією ж функцією можна очистити всю пам'ять разом, набравши «kill(all)»; після цього нумерація осередків знову піде з одиниці. Необхідно іноді це робити, тому що імена змінних у сеансах роботи можуть повторюватися. (%i9) kill(x); (%o9)
(%i10) x + y; (%o10)
(%i11) kill(all); (%o0) (%i1) x + y + t; (%o1) y + x + t Для завершення роботи із системою застосовується функція quit();, а переривання процесу обчислень здійснюється натисканням комбінації клавіш Ctrl+C (після чого варто ввести:q для повернення в звичайний режим роботи). Довідка про ту або іншу функцію виводиться по команді describe(iM1 я функції). При роботі в графічній оболонці XMaxima, можна скористатися пунктом меню help. Процедура example(iM^ функції) демонструє приклади використання потрібної в цей момент функції. Версія, яка існує на момент виходу даного посібника - 5.14.0, і робота в основному ведеться над зачисткою коду для випуску вітки 6.0. Нові версії можна завантажувати на сайті http://maxima.sourceforge.net/ru/. За цією адресою знаходяться інсталяційні пакети, що призначені як для операційної системи Windows так і для Linux. 1. ЕЛЕМЕНТАРНА МАТЕМАТИКА Розділ присвячено розв'язуванню типових завдань з елементарної математики та перевірці знань, одержаних у середній школі. Вивчивши зміст розділу, студенти мають опанувати основні прийоми тригонометрії та планіметрії, розв 'язування алгебраїчних і логарифмічних нерівностей та рівнянь, а також навчитися складати рівняння. 1.1. Тригонометрія Тригонометрія (від грецького trigonon - трикутники й metros - виміряти), розділ математики, у якому вивчаються тригонометричні функції та їхні застосування щодо геометрії. Тригонометричні функції - один із найважливіших класів елементарних функцій. Для визначення тригонометричних функцій зазвичай розглядають коло одиничного радіуса із двома взаємно перпендикулярними діаметрами A'A і B'B (рис. 1.1). Від точки А вздовж кола відкладаються кути, що вважаються позитивними, якщо відкладаються в напрямку від А до В (проти руху годинникової стрілки), і негативними, якщо вони відкладаються в напрямку від А до B' (за рухом годинникової стрілки). Проекцію OQ радіуса OC на діаметр B'B називають синусом кута a(OQ = sin а). Проекція OP радіуса OC на діаметр A'A називається косинусом кута a(OP = cos а).
Тригонометричні функції cosa та sina не можуть за абсолютною величиною перевищувати 1, тобто |cos«| < 1, |sin«| < 1. З того, що радіус кола дорівнює одиниці, випливає, що sina та cos ^ можна розглядати як синус і косинус кута. Узагалі під аргументом тригонометричних функцій прийнято розуміти число, яке можна розглядати геометрично як радіанну міру кута. Для гострих кутів а (0<а<п/2), і тільки для них, можна розглядати: sin а - як відношення між протилежним до кута а катетом і гіпотенузою; cosa- як відношення між прилеглим до кута а катетом і гіпотенузою; tgа - як відношення між протилежним і прилеглим до кута а катетів; ctgа - як відношення між прилеглим і протилежним до кута а катетів; sec а - як відношення між гіпотенузою й прилеглим до кута а катетом; cosec а - як відношення між гіпотенузою й протилежним до кута а катетом. Дуга AB кола називається 1-ою його чвертю, відповідно дуга BA' - 2-ою, A'B'- 3-ою, B'A - 4-ою чвертями. Для 1-ої чверті: cosa>0, sina>0; 2-ої чверті: cosa<0, sina>0; 3-ої чверті: cosa<0, sina<0; 4-ої чверті: cosa>0, sina<0. Крім того, cosa- парна функція: cos (-a) = cosa, а sina- непарна функція: sin (-a) = -sina. За допомогою основних тригонометричних функцій можна визначити інші тригонометричні функції: тангенс tga= sina / cosa, котангенс ctga= cosa / sina, секанс seca= 1/cosa, косеканс cosec a = 1/sina. При цьому tga і sec a визначаються тільки для тих кутів а, для яких cosa^ 0; а ctga і cosecaдля тих а, для яких sina^ 0; функція seca - парна, а функції coseca, tga і ctga- непарні. Ці функції також можуть бути представлені геометрично відрізками прямих (рис. 1.1): tga = AL, ctga = BK, seca = OL, cosec a = OK (для гострих кутів a і відповідними відрізками для інших кутів). Із цим геометричним розумінням пов'язане й походження назв тригонометричних функцій. Так, латинське tangens означає дотичну (tga зображується відрізком AL дотичної до кола), secans - січну (sec а зображується відрізком OL січної до кола). Назва «синус» (латинською sinus - вигин, пазуха) являє собою переклад арабського «джайб», що є, напевно, перекручуванням санскритського слова «джива» (буквально - тятива лука), яким індійські математики позначали синус. Назви «косинус», «котангенс», «косеканс» являють собою скорочення терміна complementi sinus (синус доповнення) і йому подібних, що виражають той факт, що cosa, ctga і coseca дорівнюють відповідно синусові, тангенсові й секансові аргументу кута, додаткового до a: cosa= sin (900- a); ctga= tg (900- a); coseca= sec (900- a). Точка C служить кінцем дуг a a + 2п, a + 4п,... (2п - довжина кола), тому всі тригонометричні функції є періодичними. Головним періодом функцій sina, cosa, seca, coseca є число 2п (кут у 3600), а головним періодом tga і ctga- число п (кут у 1800). Графіки тригонометричних функцій див. на рис. 1.2. Значення тригонометричних функцій того самого аргументу пов'язані між собою співвідношеннями: БІи2а + соБ2а = 1; 1§2а + 1 = Бес2а; С^2а + 1 = соБес2а. Для значень аргументу кратних 300 і 450 значення тригонометричних функцій можуть бути отримані з геометричних розумінь (табл. 1.1 і табл. 1.2). Для інших значень аргументу значення функцій наведені в додатку А.
Для великих значень аргументу можна користуватися так званими формулами зведення, що дозволяють виразити тригонометричні функції будь-якого аргументу через тригонометричні функції аргументу а, що задовольняє співвідношенню 0 < а < п або навіть 0 < а < п/2, що спрощує складання таблиць і побудову графіків тригонометричних функцій, а також користування ними. Ці формули наведені в таблиці 1.3:
Найважливішими тригонометричними формулами є формули, що виражають тригонометричні функції суми або різниці значень аргументів через тригонометричні функції цих значень: sin(x ± y) = sinx-cosy ± cosx-siny; tg(x ± y) = (tgx ± tgy)/(1 + tgx-tgy); cos (x ± y) = cosx-cosy ± sinx-siny; ctg(x ± y) =(ctgx-ctgy + 1)/(ctgx ±ctgy). Знаки в лівій і правій частинах усіх формул погоджені, тобто верхньому (нижньому) знакові ліворуч відповідає верхній (нижній) знак праворуч. Із цих формул випливають формули для тригонометричних функцій кратних аргументів, наприклад: sin 2a=2sinacos a= (2tga) / (1+tg a); cos2a= cos2a- sin2a= 2 cos2a- 1 = 1-2 sin2a; tg 2a= (2 tga) / (1-tg2a); ctg2a= (ctg a-1) / 2ctga; 3 2 3 0 0 sin3a= 3sina-4sin a= 3cos a■ sina-sin a=4sinasin(60 -o)-sin (60 +a); cos3a= 4cos3a-3cosa= cos3a-3cosasin2a; tg3a= (3tga-tg3a) / (1-3tg2a); tg 3a= tga tg (600-a) ■ tg (600+a); ctg3a= (ctg a-3ctga) / (3ctg a-1); sin4a= 8cos asina-4cosasina; cos4a= 8cos4a-8cos2a+1; tg4a= (4tga-4tg3a) / (1-6tg2a+tg4a); ctg4a= (ctg4a-6ctg2a+1) / (4ctg3a-4ctga). Часто бувають корисними формули, що виражають степені sinaTa cosa простого аргументу через sinaTa cosa кратного, наприклад: 2 sin a = (1 - cos2a) / 2; cos a = (1 + cos2a) / 2; 2 2 2 2 sin a = 1 / (1+ctg a) = tg a / (1+tg a); 2 2 2 2 cos a = 1 / (1+tg a) = ctg a / (1+ctg a); sin3a =% (3sina - sin3a); cos3a =% (cos3a +3cosa); sin4a =1/8 (cos4a - 4cos2a+3); cos4a =1/8 (cos4a + 4cos2a+3). 2 2 2 2 Формули для sin a, cos a, tg a, ctg a можна використовувати для визначення значень тригонометричних функцій половинного аргументу: 22 sin a/2 = (1-cosa) / 2; cos a/2 = (1+cosa) / 2; 2 2 2 2 2 tg a/2 = (1-cosa) / (1+cosa)=sin a / (1+cosa) =(1-cosa) / sin a; 2 2 2 2 2 ctg a/2 = (1+cosa) / (1-cosa)=sin a / (1-cosa) = (1+cosa) / sin a. Бувають також корисними такі співвідношення між тригонометричними функціями: sin a= (2 tg a/2) / (1 + tg2a/2); 1 + cos a = 2 cos2a/2; sin2a= tg2a/ (1+tg2a)2= 1 / (1+ctg2 a)2; 1 - cosa = 2 sin2a/2; cos a= (1- tg2a/2) / (1+ tg2a/2); 1 + tg2a = 1 / cos2a, a^n(2«+1)/2; 2 2 2 2 2 2 2 cos a= 1 / (1+ tg a) = ctga/ (1+ctg a); 1+ ctg a =1 / sin a, a^ nn Сума або різниця тригонометричних функцій різних аргументів можуть бути перетворені на добутки за формулами: sinx+siny=2sin((x+y)/2)-cos((x-_y)/2); tg x - tgy = (sin (x -y))/ (cos x cos y); sinx-sin y=2cos((x+y)/2)-sin((x-y)/2); сtg x + d:g y = (sin (x+y))/(sin x sin y); cos x+cosy=2cos((x+y)/2)-cos((x-y)/2); сtg x - сtg y = - (sin (x-y))/(sin x sin y); cos x-cos y=-2sin((x+y)/2)sin ((x-y)/2); tg x + d:g y = (cos (x-y))/(cos x sin y); tg x + tg y = (sin (x+y))/(cos x cos y); ctg x - tg y = (cos (x+y))/(sin x cos y). Навпаки, добутки тригонометричних функцій можуть бути перетворені на суму або на різницю за формулами:
sin x sin y = %(cos (x-y) - cos (x+y)); cos x cos y = %(cos (x-y)+ cos (x+y)); sin x cos y = %(sin (x-y)+ sin (x+y)). Похідні всіх тригонометричних функцій виражаються через тригонометричні й алгебраїчні функції: (sin x) = cos x; (cos x) = -sin x; ' 2 (tg x) = 1/cos x; '2 (ctg x) = - 1/sin x; При інтегруванні тригонометричних функцій виходять тригонометричні функції або їхні логарифми: J sin xdx = - cos x + C; Jtgxdx = - ln |cos x| + C; dx I—— = — ctgx + C;
J C1 sin2 x dx x tgx Jcos xdx = sin x + C; Jctgxdx = ln I sin x| + C; dx J — = tgx + C; cos x
dx у 2 + 4 у
Рівняння x = sin у визначає «у» як багатозначну функцію від «х». Функція «у» є зворотною стосовно синуса й позначається як у = arcsin x. Аналогічно визначаються функції, зворотні стосовно косинуса, тангенса, котангенса, секанса й косеканса: arccos x, arctg x, arcctg x, arcsec x, arccosec x відповідно. Усі ці функції називаються зворотними тригонометричними функціями. sin(arcsin a) = a; arcsin (sina) = a, aє [-n/2; n/2]; cos(arccos a) = a; arccos(cos a) = a, a є [0; n]; tg (arctg a) = a; arctg (tg a) = a, a є [-n/2; n/2]; ctg (arcctg a) = a; arcctg (ctg a) = a, a є [ 0; n]; arcsin(sina) = a - 2nn, aє [-n/2 +2nn;n/2+2nn]; arcsin(sina) = (2n+1)n - a, aє [n/2+2nn;3n/2+2nn]; arccos (cosa) = a-2nn, aє [2nn;(2n+1)n]; arccos (cosa) = 2nn-a, aє [(2n-1)n; 2nn]; arctg(tga)= a-nn, aє(-п/2 +nn;n/2+nn); arcctg(ctga) = a -nn, aє (nn; (n+1)n). Співвідношення між зворотними тригонометричними функціями: arcsina = -arcsin (-a)= п/2-arccosa = arctg a/V(1-a2); arccosa = n-arccos(-a)=n/2-arcsin a = arc ctga/V(1-a2); arctgа = -arctg(^) = п/2 ^гс^а = arcsin (а/^(1+а2)) = arccos(1/V(1+а2)); arcctg а = п^ге^^а) = arccos (а/^(1+а2)); arctg а = arc^^^); arcsin а + arccos а = n/2; arcctg а + arctg а = п/2. Для обчислення тригонометричних функцій у Ma"ima достунні нрямі та зворотні тригонометричні функції: синус (sin т), косинус (cos т), тангенс (tan x), котангенс (cot x), арксинус (asin x), арккосинус (acos x), арктангенс (atan x), арккотангенс (acot x). Окрім них є менш відомі функції - се- конс (sec x = 1/cos x) і косеконс (csc x = 1/sin x), а також гінерболічні функції
), гінерболічний косинус (cosh x =
e + e e — e. ), гінерболічний тангенс (tan x =------------- —), гінерболічний котангенс / ex + e~x ч (cot = —7 ). e + e
(%il) sin (%pi/ 6) A2 +cos (%pi/6) A2; (%ol) 1 (%i2) sec(%pi/3); (%o2) 2 (%i3) asin(1/2); % p і (%o3) -- (%i4) asin (sqrt (3) /2); %pi (%o4) -- Рис. 1.3. Фрагмент обчислень тригонометричних функцій у Mаximа Maxima легко оперує тригонометричними виразами. Так, функція trigexpand використовує формули перетворення сум двох кутів для представлення введеного виразу в найбільш простому вигляді: (%І5) sin (u+v)*cos(u)Л3; з (%о5) cos(u) sin(v + u) (%І6) t. rigexpand (%); з (%об) cos(u) (cos (u) sin(V) + sln(U) COS (V)) Функція trigreduce перетворить тригонометричний вираз до суми елементів, кожен з яких містить тільки єдиний sin або cos: (%І7) trigreduce(%); sii2(v + 4 u)+sin(v - 2 u) 3 sln(v + 2 u)+3 r) (%o7) ---------------------- +---------------------- 8 8 Функція trigsimp використовує тотожність sin x + cos x = 1, а також тотожність cosh x - sinh x = 1, щоб спростити вирази, які містять tan, sec і тому подібні у вирази, які містять sin, cos, sinh, cosh. Функції ratsimp і radcan також можуть сприяти спрощенню результату. Тригонометричне рівняння - алгебраїчне рівняння щодо тригонометричної функцій невідомого аргументу. Для розв'язування тригонометричних рівнянь, користуючись різними співвідношеннями, їх перетворюють до такого виду, щоб можна було визначити значення однієї із тригонометричних функцій шуканого аргументу. Після цього розв'язки тригонометричних рівнянь знаходять за допомогою зворотних тригонометричних функцій. Наприклад, вираз sin х + sin 2x + sin 3х = 0 можна перетворити до вигляду: 2 sin 2x cos х + sin 2x = 0, або sin 2x (2cos х + 1) = 0. Звідки: sin 2x = 0, або cos х = -1/2. Це дає розв'язки: х = arcsin 0 = 0+2nn і х = arccos (-1/2) = 2/3n(3n ±1), де n - довільне ціле число (позитивне або негативне). Для узагальнення розв'язку тригонометричних рівнянь використовують формули: sin x = m; |m| ^ 1, x = (-1)n arcsin m + nn, пє Z; якщо sin x =1, то x = n/2 + 2nn; якщо sin x = 0, то x = nn; якщо sin x = -1, то x = -n/2 + 2 nn. cos x=m; |m|< 1, x = ± arccos m + 2nn; якщо cos x = 1, то x = 2nn; якщо cos x = 0, то x = n/2+nn; якщо cos x = -1, то x = n+ 2nn. tg x = m, x = arctg m + nn. ctg x = m, x = arcctg m +nn. Для розв'язування тригонометричних рівнянь використовують такі прийоми алгебри, як розкладання на множники та заміна. Наприклад, вираз sin2x-V3cos x = 0 за допомогою такого розкладання перетворюється на вираз 2sin x cos x - VJcos x = 0, у якому можливо винести cos x за дужки й розв'язати рівняння: cos x(2 sin x - >/з) = 0. В якості тригонометричної заміни використовують sin x/2 = 2t/(1+t) та cos x/2 = (1-t2)/(1+t2), де t=tgx. Для розв'язування тригонометричних нерівностей використовують формули: якщо sin а < m, то 2пп+а1 < а < а2+ 2пп; якщо sin а > m, то 2пп+а2 < а< (а1+2п)+ 2пп; якщо cos а < m, то 2пп + а1 < а< а2+2пп; якщо cos а > m, то 2пп+а2< а< (а1+2п) + 2пп; якщо tg а>(<) m, то nn+ arctg m <а< arctg m + nn; якщо ctg >(<) m, то nn+arcctg m < а< arcctg m +nn. Наприклад, вираз sin а < 1/2 можна перетворити на: 2nn +5п/6 <а< 13n/6+2nn. А вираз cos а > - >/2/2 можна перетворити на: 2nn+5n/4 <а< 11п/4 +2nn. Приклади Приклад 1. Укажіть кількість і суму розв'язків рівняння в інтервалі (п Л (3к \ [00;3600]: sin3(n-x) + sin3 x = cos4 — + x -cos4(x -n). Л, Знайдемо область дозволених значень (ОДЗ): x є R. За формулами зведення: sin3 x + cos3 x = sin4 x - cos4 x. За формулами скороченого множення: a3 + b 3 = ( a + b)• (a2 -ab + b 2 ); a4 - b 4 = ( a 2 - b2) • (a2 + b 2 ). (sin x + cos x)(sin x - sin xcos x + cos x) = (sin x - cos x)(sin x + cos x). За основною тригонометричною тотожністю sin2 x + cos2 x = 1, та з урахуванням формули a2 - b2 = (a - b)•(a + b) одержуємо рівняння: (sin x + cos x)(1 - sin x cos x) - (sin x - cos x)(sin x + cos x) = 0, (sin x + cos x)(1 + cos x - sin xcos x - sin x) = 0, (sin x + cos x)(1 + cos x - sin x • (cos x +1) = 0, (sin x + cos x)(1 + cos x)(1 - sin x) = 0. Розглянемо 3 випадки в інтервалі [00; 3600]: 1) sin х + cos х = 0. Розділимо на cos x: п 3 п 7 п tg х = - 1; х = -— + пк, кє Z. х1 = — (при к = 1) і х2 = (при к = 2). 2) 1 + cosх = 0, cos х = -1; х = п + 2пп, nє Z. х3 =п. 3) 1 - sin х = 0 ^ sin х = 1 ^ х = —+ 2пт, т є Z. х4 = —. 2 4 2 Відповідь: В інтервалі [00; 3600] усього чотири розв'язки рівняння. ^, 3п 7п п 5п 3п. Сума розв'язків х + х2 + х3 + х4 =------ 1----- І п І— =-- 1--- = 4п. ► 1 2 3 4 4 4 2 2 2 Приклад 2. Розв'язати рівняння: sin2 2 х + sin2 3х + sin2 4 х + sin2 5 х = 2. А Знайдемо область дозволених значень (ОДЗ): х є R. Застосовуючи формули зниження ступеня, зведемо це рівняння до більш простого вигляду: 1(1 - cos4x) +1(1 - cos6x) +1(1 - cos8x) +1(1 - cos10x) = 2, 1 - cos4 х +1 - cos6 х +1 - cos8 х +1 - cos10 х = 4, cos4 х + cos6 х + cos8 х + cos10 х = 0. Звідси, використовуючи формулу перетворення суми косинусів у добуток, одержуємо: 4 х + 6 х 4 х - 6 х _ 8 х + 10х 8 х -10 х. 2cos----------- cos------------ І 2cos----------- cos----------- = 0, 2 2 2 2 2cos5x cos x + 2cos9 x cos x = 0 або cos x(cos5 x + cos 9 x) = 0. Розглянемо 2 випадки: п 1) cos x = 0 ^ x =—+пк; 12 2) cos 5 x + cos 9 x = 0, отже, знову використовуючи формулу перетворення суми косинусів у добуток, маємо: 5 х + 9 х 5 х - 9 х _ cos---------- cos---------- = 0 ^ cos7х • cos2х = 0 ^ 2 2 _ ч _ _ _ п, п п к 2а) cos 7х = 0 ^ 7х = —+пк ^ х2 =---------- 1--- 2 2 14 7 2б) cos2х = 0 ^ 2х = п + пк ^ х, = — + —k-. 2 3 4 2 Таким чином, з урахуванням ОДЗ, одержуємо відповідь: п, п п к п п к, „. х = —+ пк, х2 =---- 1----, х3 = —І-----, к є Z. ► 1 2 2 14 7 3 4 2 Приклад 3. Розв'язати рівняння: 10 cos 2х + 8 = tgx. п А Знайдемо ОДЗ: cosх Ф 0, тобто х Ф ±— + 2пк, к є Z. Уведемо нову змінну t = tgx. О • 0 1 - tg2 X 1 -12. И Оскільки cos 2 x =----- — =--- -, рівняння прииме вигляд: 1 + tg2 x 1 +1 1 — 12 + 8 = t або 10-(1 — t2) + 8(1 + 12) = t -(1 + 12) 10 — 10t2 + 8 + 8t2 — t — t3 = 0 ^ t3 + 2t2 +1 —18 = 0. Розкладемо дане рівняння в такиИ спосіб: t3 — 2t2 + 4t2 — 8t + 9t —18 = 0; 12(t — 2) + 4t(t — 2) + 9(t — 2) = 0 ^ (t — 2)(t2 + 4t + 9) = 0. КвадратниИ тричлен у других дужках не має діИсних розв'язків. Отже, рівняння має тільки один розв'язок. ЗнаИдемо розв'язки вихідного рівняння: tgx = 2 ^ x = arctg2 + nk, k є Z. ДодатковиИ випадок розглядати не треба, тому що cos х Ф 0. Відповідь: х = arctg2 + nk, k є Z. ► Приклад 4. Розв'язати рівняння: tgx — sinх = 1 — tgx - sinх. п Л ЗнаИдемо ОДЗ: cos х Ф 0, тобто х Ф ±— + 2nk, k є Z. Перетворимо рівняння в такиИ спосіб: tgx + tgx - sin х = 1 + sin х tgx(1 + sin х) = 1 + sin X (1 + sin x)tgx — (1 + sin х) = 0 (1 + sin x)(tgX — 1) = 0. Розглянемо 2 випадки: п 1) (1 + sin х = 0) ^ (sin x = —1) ^ (х = —- + 2nk); у цьому випадку вихідне рівняння розв'язків не має, тому що ці розв'язки не входять до ОДЗ; п 2) (tgx — 1 = 0) ^ (tgx = 1) ^ (х = — + nk); ці значення входять до ОДЗ. При розв'язанні цього прикладу в Maxima використовується функція solve. Maxima попереджає, що деякі розв'язки можуть бути загублені, оскільки не враховується періодичність функціИ і навпаки, можуть бути розв'язки, що не входять в ОДЗ. (%І8) solve ([tan (х) -sin (х) =l-t.an (х) *sin (х) ] г [н]); "soive' is using arc-trig functions to get a solution. Some solutions will be lost. (%o8) [ x=---,x =----- ] 4 2 п Відповідь: x = —+nk, kє Z.► 4 1.2. Індивідуальне завдання № 1.1 Студент повинен розв'язати одну з наведених нижче задач, вибравши її за своїм номером у журналі групи. Обчислити значення виразу:
tg550 - tg350 ; tg200 ; sin910 - sin10 W2cos460 + V2sin440 10sin400 • sin500 ; cos100 _ П П
7. tg— + ctg—; 12 12
' 9f 9. arcsin к 11. arcsin(cos—f); 2. cos (arctg2>/6); arcsin1 + arccos— 5 j к 6. tg ^ arctg-2 + arctg-3 j; 8. cos (arcctg (-W3)); m Г 12п j 10. arccos і sin——— І; t_ cosa-cose p aao 12.--------------- —, якщо a-e= 90;
sin a + sin в
, якщо sin 4a = 0,4;
2 1 14. 9cos(a + e), якщо cosa = —, sinв = -~, ає Укажіть у градусах суму розв'язків рівняння:
= 4 - cos2 (f - 3x), що належать проміжкові
17. cos x + >/з sin x = V2, що належать проміжкові
Укажіть кількість розв'язків рівняння: 2. - 3 що належать проміжкові
19. 1 + ctgx = cos x +----, що належать проміжкові sin x 20. 1 + ctgx = cos x +—1—.
|
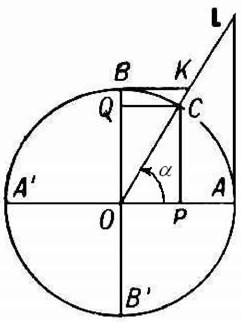Рис. 1.1. Тригонометричне коло
