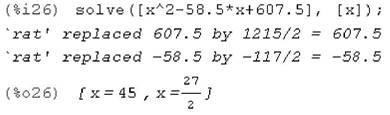Приклади. Приклад 1. Розв'язати задачу: Два туристи йдуть назустріч один одному з пунктів А і В
Приклад 1. Розв'язати задачу: Два туристи йдуть назустріч один одному з пунктів А і В. Перший виходить з А на 6 годин пізніше, ніж другий з В, і при зустрічі в пункті С виявляється, що він пройшов на 12 км менше за другого. Продовжуючи після зустрічі шлях з тією ж швидкістю, перший приходить у В через 8 годин після зустрічі, а другий у А - через 9 годин. Визначити відстань АВ і швидкість обох пішоходів.
^ Нехай у15 у2 (км/год) - швидкості першого і другого пішоходів, а відстань АВ позначимо за 5. Зобразимо рух пішоходів графічно. Оскільки ділянку СВ перший пройшов за 8 годин, то ВС = 8у 1. Другий пройшов відстань СА за 9 годин, тому АС = 9у2. З умови задачі маємо: АС +12 = ВС ^ 9у2 +12 = 8У1. Виразимо час, витрачений пішоходами від початку руху до їхньої зу.. АС 9у2 ВС 8У, стрічі: г1 =----- = —-, і2 =------- = —1.
V
Перший вийшов на 6 годин раніше, тому: і1 + 6 = і2
V,
і розв яжемо рівняння:
8 2 2 4 9а + 6 = — ^ 9а + 6а - 8 = 0 ^ а1 = —, а2 = —. а 3 3
Але а - це відношення швидкостей, а значить його значення більше нуля. Одержимо систему: v2 = 2 V"" 3 9^ -12 = 8v1 Виходить, 5 = АС + ВС = 9^ + 8^ = 84. Відповідь: 5 = 84, V = 6, v2 = 4. ► Приклад 2. Розв'язати задачу: Дві труби, працюючи одночасно, наповнюють басейн за 12 годин. Якщо працює тільки перша труба, то вона наповнює басейн на 10 годин повільніше, ніж тільки друга. За скільки годин наповнює басейн тільки друга труба? ^ Нехай х (м3) - об'єм басейну і і (год.) - час наповнення басейну тільки другою трубою. Тоді тільки перша труба наповнить басейн за і +10 годин. х х
Знаходимо продуктивність цих труб: Ы2 = —, N1 = —— роботи з загальною продуктивністю N1 + N2 заповнюється весь басейн: ^х х Л — + • 12. Скоротивши на х і перетворивши останнє рівняння отрима- V г г +10) ємо: г (г +10) = (2г +10)12. Розкриємо вирази у дужках і перенесемо всі доданки з правої частини рівняння в ліву. Одержимо квадратне рівняння: х= г2-14г-120 = 0 ^ г1 = 20, г2 = -6. Оскільки час вимірюяється у позитивних значеннях, то другий корень рівняння не підходить. Відповідь: г = 20 год. ► Приклад 3. Розв'язати задачу: В ательє надійшли відрізи чорної, зеленої і синьої тканин. Хоча зеленої тканини було на 9 м менше, ніж чорної, і на 6 м більше, ніж синьої, вартість відрізів була однаковою. Скільки метрів тканини було в кожному відрізі, якщо відомо, що вартість 4,5 м чорної тканини дорівнює загальній вартості 3 м зеленої і 50 см синьої'?
А Нехай хч, х3, хс - кількість чорної, зеленої і синьої тканин відповідно. Відомо: хч - х3 = 9, х3 - хс = 6. Використовуємо формулу: Сі = —, де Сі - хі ціна тканини, Уг - вартість г-го відрізу, Хг - кількість г-ої тканини. З умови задачі y4 = y3 = yc = y. Одержимо Сч =—, С3 = —, Сс = — ХЧ Х3 хс ціни тканин. Складемо рівняння, що зв'язує ці вартості: 4,5СЧ = 3С3 + 0,5Сс ^ ^^^^y = ^ +. хч хз хс Виразимо х3 і хс через хч: х3 = хч - 9, хс = х3 - 6 = хч -15. Скоротивши на y підставляємо в останнє рівняння: 4 5 3 0 5 2 =------------ + —1— ^ хч - 58,5хч + 607,5 = 0, причому хч Ф 0; 9; 15. хч хч 9 хч -15 4... Корені квадратного рівняння: хч = 45, хч = 13,5. Розглянемо обидва випадка: 1. якщо хч = 45, то х3 = 36, хс = 30. 2. якщо хч = 13,5, то х3 = 4,5, хс =-1,5. Другий випадок неможливий, тому що кількість тканини вимірюється у позитивних значеннях. Відповідь: надійшло 45м чорної, 36м зеленої і 30м синьої тканини. ► Приклад 4. Знайти розв'язок рівняння у=х2-58,5х+607,5 створеного у попередньому прикладі. АЗастосуємо функцію solve програми Maхima.
Вивчивши зміст розділу, студент має опанувати основні прийоми розв'язування систем лінійних алгебраїчних рівнянь, як вручну так із застосуванням вільного програмного забезпечення. 2.1. Визначення матриці
Матрицею розміром т*п називається сукупність т-п чисел, розташованих у вигляді прямокутної таблиці з т рядків і п стовпців. Цю таблицю зазвичай беруть у круглі дужки. Наприклад, матриця може мати вигляд:
Для стислості матрицю можна позначати однією заголовною літерою, наприклад, А або В. У загальному вигляді матрицю розміром тхп записують так: Ґ ап ах1... а±пЛ а21 а22 ••• а2 п А = V ат1 ат 2 • • • ~тп у Числа, що складають матрицю, називаються елементами матриці. Елементи матриці зручно позначати літерою із двома індексами ау: перший указує номер рядка, а другий - номер стовпця. Наприклад, а23 - елемент розташований у 2-му рядку 3-го стовпця.
|

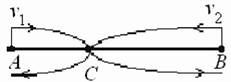 Рис. 1.26. Рух пішоходів
Рис. 1.26. Рух пішоходів