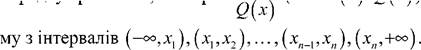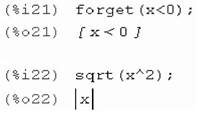Приклади. Приклад 1. Дано 2 сторони трикутника а, Ь і медіана тс, проведена до сторони с
Приклад 1. Дано 2 сторони трикутника а, Ь і медіана тс, проведена до сторони с. Знайти сторону с. А Добудуємо трикутник ABC до паралелограма АСВК. При цьому KC = 2 • mc. За властиві- 2 2 2 2 стю паралелограма: 4mc + c = 2b + 2a. Звідси 2 2 2 одержуємо: c = 2b + 2a -4mc. I 2 2 2
Відповідь: c = ^2a + 2b - 4mc.► Приклад 2. В колі проведені 3 хорди: АЫ = 6 см, МВ = 4 см, МС = 1 см. Хорда МВ поділяє вписаний кут АМС навпіл. Знайти радіус кола. А Нехай кут АМВ = а. За теоремою косинусів із трикутника АМВ маємо:
АВ2 = АМ2 + МВ2 - 2 АМ • ВМсоб а = 52 - 48соб а. Аналогічно з трикутника ВМС маємо: ВС2 = ВМ2 + МС2 -2ВМ • МСсоБа = 17- 8соБа. Відрізки АВ і ВС рівні як хорди, що стягають рівні дуги, тому віднімемо з першого рівняння друге й одержимо:
AB1 = 52 — 48cosa = 52 — 48-- = 52 — 42 = 10,
Трикутник АМВ, є вписаним у коло, отже, радіус кола можна знайти за допомогою теореми синусів:
f 7 Y
18 J
Приклад 3. У сектор радіуса Я з центральним кутом а вписане коло. Знайти радіус кола. Дано: АВ = АС = Я, кут ВАС = а. Знайти: ОН = г. Л Оскільки центри кругів і точки перетину розташовані на одній прямій, то АО = Я - г. Розглянемо трикутник АОН (він прямокутний, а тому що кут ОНА = 900): кут НАО = — з рівності трикутників АОН і АОМ (тому що ОН=ОМ=г, АН=АМ як відрізки дотичних, проведених з однієї точки, сторона АО - спільна). Оскільки, синус кута прямокутного трикутника дорівнює відношенню
катета, що розташований напроти гіпотенузи, маємо: а OH r а fIi • а.а sin— =----------------------- = ^ (sin— (R — r) = r) ^ (R - sin-- r - sin— = r) ^ 2 AO R — r
. а.а ч (R - sin— = r - sin—+ r) 2 2 . а R sin— Відповідь: r =---------- —.► а 1 + sin— 2
Приклад 4. Основи трапеції 5 дм і 40 см. Знайти довжину відрізка, що з'єднує середини діагоналей. Л Нехай АВСБ - трапеція, точка Р - середина діагоналі АС, точка К - середина діагоналі ВО. Точки Р й К розташовані на середній лінії ЕР трапеції. З того, що ЕК - середня лінія трикутника АВО, а середня лінія трикутника - це відрізок, що з'єднує середини двох сторін трикутника, паралельний третій стороні і дорівнює іі половині, випливає, що EK = — см = 25 см. Аналогічно, EP = — см = 20 см, оскі- льки ЕР є середньою лінією А ABC. Отже, PK = EK - EP = 25 - 20 = 5 см. Відповідь: 5 см. ► 1.4. Індивідуальне завдання № 1.2 Студент повинен розв'язати одну з наведених нижче задач, вибравши її за своїм номером у журналі групи. Знайти: 1. Синус кута B трикутника ABC, якщо AC = 4 см, BC = 5 см, cos A = —; 2. Довжину сторони ромба, якщо довжини діагоналей ромба відносяться як 1:2, а площа ромба дорівнює 12 см; 3. Площу кільця, якщо у коло вписаний правильний трикутник, площа якого дорівнює 9л/з см2, і в трикутник вписане коло; 4. Площу трикутника ABD, якщо в трикутнику ABC кут при вершині C дорівнює 1350, AC = 6 см, висота BD = 2 см; 5. Синус кута A трикутника ABC, якщо AC = 4см, BC = 7см, AB = 5см; З 6. Довжину сторони AB трикутника ABC, якщо BC = 9 см, cos C = —, =2 sin A = —; 7. Відстань від центра кола до хорди, яка стягає дугу в 600, якщо радіус кола Зл/27 см; 8. Довжину першої діагоналі, якщо друга діагональ паралелограма, довжиною 4л/6 см, утворює з основою кут 600, а перша діагональ утворює з тією ж основою кут 45; 9. Відстань від центра кола до хорди, якщо в колі, площа якого дорівнює 6,25псм, проведена хорда довжиною 3 см; 10. Суму довжин катетів прямокутного трикутника, якщо в трикутнику довжина гіпотенузи дорівнює 20 см, а радіус вписаного кола - 4 см; 11. Довжину сторони ромба, якщо площа ромба дорівнює 18 см, а гострий кут 300;
12. Відстань між точкою M і основою H висоти CH у прямокутному трикутнику ABC, якщо катет AC = 7 см і медіана CM = 7 см, проведена до гіпо 13. Відношення у якому поділяє площу трапеції відрізок довжини 5 см, що з'єднує бічні сторони рівнобедреної трапеції, якщо цеИ відрізок паралельниИ її основам, рівним 2 см і 7 см; 14. Периметр рівнобедреного трикутника із кутом 1200, що вписаниИ у коло радіуса 10 см; 15. Площу спільної частини кіл радіуса 6 см, якщо O1 і O2 - центри кіл, O1O2 = 6-J2 см; 16. Площу кола, описаного навколо рівнобедреної трапеції, якщо у цієї трапеції висота дорівнює 14 см, а основи рівні 12 см і 16 см; 17. Периметр квадрата вписаного у прямокутниИ трикутник із катетами a і b, якщо квадрат має з трикутником спільниИ прямиИ кут; 18. Основи рівнобедреної трапеції з бічною стороною, рівною 17 см, що описана навколо кола діаметром 15 см; 19. Довжину відрізка дотичної обмеженою сторонами трикутника, якщо відомо, що дотична проведена до кола, вписаного в рівнобедрениИ трикутник з основою 12 см і висотою 8 см, і паралельна основі трикутника; 20. Довжини сторін AB і AC трикутника ABC, якщо BC = 8 см, а довжини висот, проведених на AC і BC, рівні відповідно 6,4 см і 4 см. 21. Довжину меншої бічної сторони трапеції, якщо її середня лінія дорівнює 10 см, одна з основ - 8 см, один із кутів трапеції дорівнює 300, а прямі, що містять бічні сторони трапеції, перетинаються під прямим кутом; 22. Висоту прямокутного трикутника проведену до гіпотенузи, якщо вона поділяє прямиИ кут у співвідношенні 1:2, а площа трикутника дорівнює 2л/3 см; 23. Площу кола описаного навколо прямокутного трикутника, якшо периметр трикутника дорівнює 24 см, а площа трикутника дорівнює 24 см2; 24. Радіус меншого кола кругового кільця, якщо Иого площа дорівнює S, а радіус більшого кола дорівнює довжині меншого кола; 25. Площу прямокутного трикутника, якщо один із Иого катетів дорівнює 15 см, а радіус кола, вписаного в трикутник, дорівнює 3 см; 26. Довжину гіпотенузи прямокутного трикутника, якщо довжини Иого сторін утворюють арифметичну прогресію з різницею 1 см; 27. Сторону a трикутника ABC, якщо катети рівні b і є, а кут А удвічі більше кута B; 28. Довжину бісектриси прямого кута, якщо катети прямокутного трикутника рівні b і є; 29. Площу рівнобедреної трапеції, що вписана у коло радіуса 3 см, якщо трапеція має кут при основі п/4 і висоту л/2 см; 30. Площу ромба ABCD, якщо радіуси кругів, описаних біля трикутників ABC і ABD, відповідно R і r; 31. Площу спільної частини кругів радіусів R і r, якщо відстань між центрами ціх двох кругів дорівнює d. 1.5. Алгебраїчні рівняння й нерівності Рівняння в математиці це аналітичний запис задачі про пошук значень аргументів, при яких значення двох даних функцій рівні. Перша з даних функцій розташована до знаку рівності, друга - після цього знаку. Аргументи, від яких залежать ці функції, називаються звичайно невідомими, а значення невідомих, при яких значення функцій рівні, - розв'язками; про такі значення невідомих говорять, що вони задовольняють даному рівнянню. Наприклад, 3х-6=0 є рівнянням з одним невідомим, а х=2 є його 2 2 розв'язком; х + у = 25 є рівнянням із двома невідомими, а х=3, у=4 є одне з його рішень. Сукупність рішень даного рівняння залежить від області М значень, що допускаються для невідомих. Рівняння може не мати рішень в області М, тоді воно називається нерозв'язним в області М. Якщо рівняння розв'язне, то воно може мати одне, два, або навіть безліч рішень. Для розв'язування рівнянь існують певні правила. Наприклад, для квадратного рівняння виду ах2+Ьх+е=0 пошук розв'язків виконують за виразом:
-Ь ± уі Ь2 - 4 ас Х,2 При цьому, якщо дискримінант О=Ь2- 4ас більше нуля, то хі^х2; якщо О дорівнює нулю, то х1=х2, а якщо О менше нуля, то дійсних розв'язків немає. Крім того, для розв'язків квадратного рівняння існує теорема Вієта, згідно якої: х1+х2 = -Ь/а; хг х2 = с/а. Для зведеного квадратного рівняння виду х2+рх+д=0 пошук розв'язків виконують за виразом: Р і Р х12 =—-д, або х1+х2 = -р; х1 • х2 = д. Якщо при розв'язуванні рівнянь маємо справу зі степенями й коренями, то бувають корисні такі формули:
(аЬ)р; аРЬР
ра = Ь ^Ьр = а;
= ар-д;
фа = р^а;
1/ р = ра: Ь р/Ь Степені деяких цілих чисел наведені у додатку Б. Часто бувають корисні формули скороченого множення й розкладання на множники: (а±Ь)2=а2±2аЬ+Ь2; (а±Ь) =а 3±3а Ь+3аЬ ±Ь; а2- Ь2=(а+Ь)(а-Ь); а3± Ь3=(а±Ь)(а2 аЬ+Ь2); (а+Ь) =а" +Ь +3аЬ(а+Ь); (а-Ь)3=а3-Ь3-3аЬ(а-Ь).
Математичні нерівності - це співвідношення між числами або величинами, що вказують, які з них більше інших. Для позначення нерівності вживається знак <, звернений вістрям до меншого числа. Так, вираз 2 > 1 і вираз 1 < 2 показують теж саме: 2 більше 1, або 1 менше 2. Іноді кілька нерівностей записуються разом (наприклад, а < Ь < с). Бажаючи виразити, що з двох чисел а і Ь одне більше (менше) другого, або дорівнює йому, пишуть: а > Ь (Ь < а) і читають: «а більше або дорівнює Ь» («Ь менше або дорівнює а»); іноді коротше: «а не менше Ь» («Ь не більше а»). Запис а # Ь означає, що числа а і Ь не рівні, але не вказує, яке з них більше. Усі ці співвідношення також називаються нерівностями. Нерівності мають багато спільних із рівностями властивостей. Так, нерівність залишається справедливою, якщо до обох її частин додати (або від обох частин відняти) те ж саме число. Так само можна множити обидві частини нерівності на те саме позитивне число. Однак, якщо обидві частини нерівності помножити на негативне число, то зміст нерівності зміниться на зворотний (тобто знак > змінюється на <, а < на >). З нерівності А < В і С < П випливає А + С < В + П і А - П < В - С, тобто однойменні нерівності (А < В і С < П) можна почленно складати, а різнойменні нерівності (А < В і П > С) - почленно віднімати. Якщо числа А, В, С і П позитивні, то з нерівностей А < В і С < П випливає також АС < ВП і А/Б < В/С, тобто однойменні нерівності (між позитивними числами) можна почленно перемножувати, а різнойменні - почленно ділити. Нерівності, у які входять величини, що приймають різні числові значення, можуть бути вірні для одних значень цих величин і невірні для інших. Так, нерівність х2 - 4х + 3 > 0 вірна при х = 4 і невірна при х = 2. Для нерівностей цього типу виникає питання про їхні розв'язки, тобто про визначення границь, у яких варто брати величини, що належать нерівностям, щоб нерівності були справедливі. Так, переписуючи нерівність х - 4х + 3 > 0 у вигляді: (х - 1)(х - 3) > 0, зауважують, що вона буде вірна для всіх х, що задовольняють одній з наступних нерівностей: х < 1, х > 3, що і є розв'язком даної нерівності. Методом інтервалів вирішуються раціональні або дробово-раціональні Р (Х) нерівності, тобто нерівності типу —0, (де Р (х) і Q (х)- багаточлени) або 0(х) нерівності, що до них зводяться. Якщо х^..., хп - усі розв'язки багаточленів Р (х) і 0 (х), розташовані в
P (x) Це означає, що коли треба визначити знак виразу —на одному з цих Q(x) інтервалів, то досить узяти будь-яку точку з цього інтервалу і розглянути зна- P(x) -. чення виразу —в цій точці. Q (x) При розв'язуванні показових нерівностей виду aj^x^>(<) a^x) у вигляді: j(x) >(<Mx) треба мати на увазі: якщо a>1, то знак не змінюється; якщо a<1, то знак змінюється. В програмі Maxima є декілька функцій, що призначені для різноманітних символьних перетворень. Функція expand - розкриває дужки й зводить вираз до канонічного виду. Наступний приклад демонструє розкриття дужок: (%І9) р1:хЛ2-1; (%о 9) х2-1 (%і10) р2:х-1; (%о 10) х-1 (%ill) expand (pl*p2); (%oll) х3-х2-х + 1 (%І12) expand((pl+p2)Л2); (%о12) х4 + 2 х3 - 3 х2 - 4 х + 4 Функцію divide можна використовувати для знаходження частки й решти від ділення одного багаточлена на іншій: (%І13) divide (pl*p2, рі); (%о13) [ х - 1, 0 J Функція gcd визначає найбільший загальний дільник багаточленів, а factor здійснює розкладання багаточлена на множники: (%І14) gcd (хА3- lf хл2-1, х-1); (%о14) х-1 (%і 15) factor (хл8-1); <%о15, (х - 1)(х + 1)(х2 + і)(х4 + і) Підстановка будь-якого виразу замість змінної здійснюється за допомогою операції =. Наприклад, замінимо всі х на 5 / z: (%І16) хЛ4+3*хЛ3-2*х, х=5/z; 10 375 625 (%ОІ6) +------------ +--- Функція rat simp виносить за дужки найбільший загальний дільник:
(%І17) ratsimp(%); 10 z - 375 z - 625 (%о17) — Використовуючи функцію assume (to assume - допускати), можна при обчисленнях ураховувати додаткові умови, що задаються нерівностями: (%і 18 (%о 18 (%і 19 (%о 19 (%І20 (%о2 0
Функція forget (to forget за допомогою assume:
|

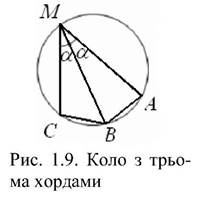
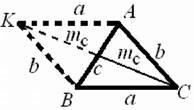 Рис. 1.8. Паралелограм ACBK
Рис. 1.8. Паралелограм ACBK
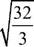
 Рис. 1.10. Сектор радіуса R
Рис. 1.10. Сектор радіуса R
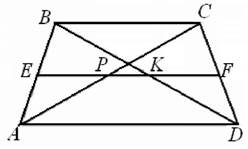 Рис. 1.11. Трапеція ABCD
Рис. 1.11. Трапеція ABCD