Теоретическая часть. 1.Знания в интеллектуальных системах
1.Знания в интеллектуальных системах Знание форма существования и систематизации результатов познавательной деятельности человека. Знание помогает людям рационально организовывать свою деятельность и решать различные проблемы, возникающие в её процессе. Знание субъективный образ объективной реальности, то есть адекватное отражение внешнего и внутреннего мира в сознании человека в форме представлений, понятий, суждений, теорий. Знание это связи и закономерности предметной области (принципы, модели, законы), полученные в результате практической деятельности и профессионального опыта, позволяющего специалистам ставить и решать задачи в данной области. В интеллектуальных системах знания представлены в виде базы знаний, где знания описаны на некотором языке представления знаний.
2. Классификация моделей представления знаний
При представлении знаний в памяти интеллектуальной системы традиционные языки, основанные на численном представлении данных, являются неэффективными. Для этого используются специальные языки представления знаний, основанные на символьном представлении данных. Они делятся на типы по формальным моделям представления знаний [1]. Наиболее часто используется на практике классификация, где модели представления знании делятся на детерминированные (жесткие) и мягкие. Детерминированные модели включают в себя логико-алгебраические модели, семантические сети, фреймы и продукционные модели. Мягкие модели включают в себя нечеткие системы, нейронные сети, эволюционные модели, гибридные системы. 3. Логико - алгебраические модели знания
В логико - алгебраических моделях знания представляются в виде совокупности правильно построенных формул какой-либо формальной системы, которая задается четверкой: S=<T, P, A, R >, где Т - множество базовых (терминальных) элементов, из которых формируются все выражения; Р - множество синтаксических правил, определяющих синтаксически правильные выражения из терминальных элементов формальной системы; А - множество аксиом формальной системы, соответствующих синтаксически правильным выражениям, которые в рамках данной ФС априорно считаются истинными; R - конечное множество отношений {r1, r2,..., rn } между формулами, называемыми правилами вывода, позволяющих получать из одних синтаксически правильных выражений другие. Простейшей логико - алгебраической моделью представления знаний являются исчисление высказываний. Развитие логики высказываний нашло отражение в исчислении предикатов первого порядка. Под исчислением предикатов понимается формальный язык для представления отношений в некоторой предметной области. Основное преимущество исчисления предикатов хорошо понятный механизм математического вывода, который может быть непосредственно запрограммирован. Предикатом называют предложение, принимающее только два значения: истина или ложь. Для обозначения предикатов применяются логические связки между высказываниями: не, Допустимые выражения в исчислении предикатов называются правильно построенными формулами (ППФ), состоящими из атомных формул. Атомные формулы состоят из предикатов и термов, разделяемых круглыми, квадратными и фигурными скобками. Предикатные символы представляются в основном глагольной формой, например: ПИСАТЬ, УЧИТЬ, ПЕРЕДАТЬ, но не только глагольной формой, а формами существительных и прилагательных, например: КРАСНЫЙ, ЗНАЧЕНИЕ, ЖЕЛТЫЙ. Предикатные символы и константы, как правило, обозначаться заглавными символами, функциональные символы и переменные строчными. В абстрактных примерах они обозначаются латинскими буквами f, g, h. В предложениях предикатной формы важны отношения и элементы. Определяя отношения, мы определяем значимость элементов выражения. Элементы могут быть предикатами и термами. Объединение нескольких связанных между собой выражений исчисления предикатов в структуры большего размера называют блокам. Эти структуры отождествляются объектами в предметной области. Для подобных схем представления знаний используется термин структурированные объекты знаний, поскольку основной упор делается на структуру представления. Рассмотрим простые примеры структуризации и эквивалентных преобразований ППФ по блочному принципу. Пример Пусть нам надо представить в виде фактов исчисления предикатов следующие предложения: Антон дал Ольге книгу. Антон программист. Ольга юрист. Адрес Антона: Гоголя, 37, кв. 7. Логическим представлением этих предложений являются следующие правильно построенные формулы: ДАТЬ (АНТОН, ОЛЬГА, КНИГА) ЗАНЯТИЕ (АНТОН, ПРОГРАММИСТ) ЗАНЯТИЕ (ОЛЬГА, ЮРИСТ) АДРЕС (АНТОН, Гоголя 37, кв. 7) В этом примере для обозначения шести понятий мы используем индивидуальные константные символы: АНТОН, ОЛЬГА, КНИГА, ПРОГРАММИСТ, ЮРИСТ и Гоголя 37, кв.7. Для удобства представления может оказаться полезным собрать все факты, относящиеся к данному понятию, в одну группу, которую мы назвали блоком. В нашем примере блок АНТОН ассоциируется со следующими фактами: АНТОН ДАТЬ (АНТОН, ОЛЬГА, КНИГА) ЗАНЯТИЕ (АНТОН, ПРОГРАММИСТ) АДРЕС (АНТОН, Гоголя 37, кв. 7) Аналогичным образом блок ОЛЬГА ассоциируется со следующими фактами: ОЛЬГА ДАТЬ (АНТОН, ОЛЬГА, КНИГА) ЗАНЯТИЕ (ОЛЬГА, ЮРИСТ)
Схема представления, в которой факты индексируются именами, обозначающими элементы или объекты предметной области, называется представлением, ориентированным на объекты. Большинство обозначений для структурирования объектов выражаются через бинарные (двухаргументные) предикаты. Для записи произвольной ППФ с помощью только бинарных предикатов можно применить простую схему эквивалентных преобразований. Чтобы, например, преобразовать трехаргументную формулу ДАТЬ (АНТОН, ОЛЬГА, КНИГА) в формулу, содержащую только бинарные предикаты, мы постулируем существование конкретного факта передачи. Назовем это множество ПЕРЕДАЧИ. Для каждого аргумента исходного предиката придумаем новый бинарный предикат, соотносящий значение этого аргумента с постулированным в исходном предикате фактом. По этой схеме формула ДАТЬ (АНТОН, ОЛЬГА, КНИГА) должна быть преобразована к виду:
ПОЛУЧАЮЩИЙ (х,ОЛЬГА) Λ ОБЪЕКТ (х, КНИГА)] Предикат ЭЛЕМЕНТ (ЭЛ) используется для выражения факта принадлежности множеству. Введение сколемовских выражений для переменных, относящихся к квантору существования наделяют постулированные нами события передачи некоторым именем ПЕР 1: ЭЛ (ПЕР 1, ПЕРЕДАЧИ) Λ ДАЮЩИЙ (ПЕР 1,АНТОН) Λ Λ ПОЛУЧАЮЩИЙ (ПЕР 1, ОЛЬГА) Λ ОБЪЕКТ (ПЕР 1, КНИГА) Таким образом, трехаргументный предикат преобразован в конъюнкцию четырех бинарных. Соотношения между ПЕР 1 и исходными аргументами предиката ДАТЬ можно выразить с помощью не предикатов, а функций над множеством ПЕРЕДАЧИ. Соответственно изменив обозначения, можно представить предложение «Антон дал Ольге книгу» такой формулой: ЭЛ (ПЕР 1, ПЕРЕДАЧИ) Λ Λ РАВ [дающий (ПЕР1), АНТОН] Λ Λ РАВ [получающий (ПЕР1), ОЛЬГА] Λ Λ РАВ [объект (ПЕР1), КНИГА] Подразумевается, что предикат РАВ обозначает синтаксическое равенство выражений. В приведенном выражении используются некоторые функции, определенные на множестве ПЕРЕДАЧИ, значения которых дают имена других объектов, составляющих ПЕР 1. Переход к представлению, в котором используются события и бинарные отношения, содержит некоторые преимущества. Из них главное для нас это модулярность. Пусть, к примеру, нам надо ввести информацию о том, когда произошел факт передачи. Прежде чем привести формулу к бинарной форме, придется ввести в предикат ДАТЬ четвертый (временной) аргумент. Подобное изменение может потребовать перемен в продукциях, связанных с предикатом ДАТЬ. Напротив, если передача книги представлена понятием в предметной области, то информацию о ней можно легко расширить, введя новые бинарные отношения, функции и ассоциированные правила. В этой части почти все суждения представлены терминами, обозначающими «события» или «ситуации», которые мы рассматриваем как элементы нашей предметной области. Нам нужно совсем немного предикатов: РАВ, чтобы выразить идентичность двух понятий; ПМ, чтобы указать, что одно множество является подмножеством другого; ЭЛ, чтобы сказать, что некоторое понятие является элементом некоторого множества. В предложениях нашего примера события состоят в том, что некие лица имеют некоторый род занятий (РЗ) и у некоторого лица есть адрес (АДР). Эти предложения можно представить так: ПЕР 1 ЭЛ (ПЕР 1, ПЕРЕДАЧИ) РАВ [(дающий (ПЕР 1), АНТОН] РАВ [получающий (ПЕР 1), ОЛЬГА] РАВ [объект (ПЕР 1), КНИГА] РЗ 1 ЭЛ (РЗ 1, РОД ЗАНЯТИЙ) РАВ [работающий (РЗ 1), АНТОН] РАВ [профессия (РЗ 1), ПРОГРАММИСТ] Р3 2 ЭЛ (РЗ 2, РОД ЗАНЯТИЙ) РАВ [работающий (РЗ 2), ОЛЬГА] РАВ [профессия (РЗ 2), ЮРИСТ] АДР 1 ЭЛ (АДР 1, АДРЕСА) РАВ [человек (АДР 1), АНТОН] РАВ [место (АДР 1), Гоголя, 37, кв. 7]. В этих блоках для связи событий с другими понятиями нами произвольно введены некоторые функции. Заметим, что приведенные блоки обладают некоторой общей структурой. Во-первых, для указания на то, что определенный объект, описываемый блоком, является элементом некоторого множества, используется предикат ЭЛ (если объект, представленный блоком, сам по себе является отдельным множеством, то для указания на то, что он был подмножеством некоторого другого множества, можно использовать предикат ПМ). Во-вторых, значения разных функций от объекта, представленного блоком, имеют отношение и к другим объектам. Поэтому введем для блоков специальное обозначение, основывающееся на этой общей структуре. В качестве сокращенной записи формулы типа РАВ [дающий (ПЕР 1, АНТОН)] мы используем такое выражение или пару: «дающий: АНТОН». Все предикаты РАВ, которые устанавливают связь между функциями от объекта, представленного блоком, и другими объектами, выражаются посредством таких пар, выписываемых под именем блока. Тогда для нашего примера получаем: ПЕР 1 дающий: АНТОН получающий: ОЛЬГА объект: КНИГА В тех системах искусственного интеллекта, которые используют блочную запись, конструкции типа «дающий: АНТОН» часто называют ячейками. Первое выражение дающий называют именем ячейки, второе АНТОН значением ячейки. Иногда значение ячейки представляет собой не константный символ (такой как АНТОН), а функциональное выражение. Эта функция, в частности, может относиться к имени ячейки другого блока. Рассмотрим, к примеру, предложения: «Антон дал Ольге книгу» и «Игорь дал ручку тому лицу, которому Антон дал книгу». Выразим эти предложения с помощью двух блоков: ПЕР 1 ЭЛ (ПЕР 1, ПЕРЕДАЧИ) дающий: АНТОН получающий: ОЛЬГА объект: КНИГА ПЕР 2 ЭЛ (ПЕР 2, ПЕРЕДАЧИ) дающий: ИГОРЬ получающий: получающий (ПЕР 1) объект: РУЧКА В этих примерах выражения получающий (ПЕР 1) и ОЛЬГА служат двумя способами называния одного и того же лица. Ниже мы рассмотрим, как можно «вычислить» функциональное выражение типа получающий (ПЕР 1), найдя значение ячейки получающий в блоке ПЕР 1.
ЭЛ [дающий (ПЕР 3), ЛЮДИ] Чтобы иметь возможность работать с такими формулами в нашей системе блочной записи, введем как некоторое псевдозначение ячейки специальную форму: (элемент множества ЛЮДИ). Такая форма служит сокращением формулы с предикатом ЭЛ. Выражение, в котором использована такая сокращенная форма, можно представлять как неопределенное описание значения ячейки.
|

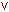 или,
или, 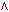 и,
и,  если, а также
если, а также  квантор существования и
квантор существования и  квантор всеобщности.
квантор всеобщности. (х) [ЭЛЕМЕНТ (х, ПЕРЕДАЧИ) Λ ДАЮЩИЙ (х, АНТОН) Λ
(х) [ЭЛЕМЕНТ (х, ПЕРЕДАЧИ) Λ ДАЮЩИЙ (х, АНТОН) Λ Значениями ячеек могут быть и переменные, относящиеся к квантору существования. Например, высказывание: «Некто дал Ольге книгу», записанное в исчислении предикатов, может содержать формулу (х) РАВ [дающий (ПЕР 3), х]. Такую переменную можно подвергнуть сколемовскому преобразованию и получить выражение вида РАВ [дающий (ПЕР 3), S]. О переменной, относящейся к квантору существования, как правило, имеется некоторая информация. В нашем примере может быть известно, что слово «некто» относится к человеку. Более удачный перевод предложения «Некто дал Ольге книгу» на язык исчисления предикатов должен содержать формулу
Значениями ячеек могут быть и переменные, относящиеся к квантору существования. Например, высказывание: «Некто дал Ольге книгу», записанное в исчислении предикатов, может содержать формулу (х) РАВ [дающий (ПЕР 3), х]. Такую переменную можно подвергнуть сколемовскому преобразованию и получить выражение вида РАВ [дающий (ПЕР 3), S]. О переменной, относящейся к квантору существования, как правило, имеется некоторая информация. В нашем примере может быть известно, что слово «некто» относится к человеку. Более удачный перевод предложения «Некто дал Ольге книгу» на язык исчисления предикатов должен содержать формулу (х) {РАВ [дающий (ПЕР3), х] Λ ЭЛ (х, ЛЮДИ)] }, или просто
(х) {РАВ [дающий (ПЕР3), х] Λ ЭЛ (х, ЛЮДИ)] }, или просто


