Гипергеометрическое распределение.
Дискретная случайная величина Х имеет гипергеометрическое распределение с параметрами n, M, N, если она принимает значения 0, 1, 2, m, …, min(n, M) с вероятностями
Гипергеометрическое распределение имеет случайная величина X = m – число объектов, обладающих заданным свойством, среди n объектов, случайно извлеченных (без возврата) из совокупности N объектов, М из которых обладают этим свойством. Теорема. Математическое ожидание случайной величины Х. имеющей гипергеометрическое распределение с параметрами n, M, N, есть Случайную величину X = m, распределенную по биномиальному закону (47), можно интерпретировать как число m объектов, обладающих данным свойством, из общего числа n объектов, случайно извлеченных из некоторой воображаемой бесконечной совокупности, доля р объектов которой обладает этим свойством. Поэтому гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов, М из которых обладают этим свойством. Можно показать, что при Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных исследований, и в других областях.
|
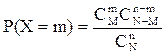(53) где 
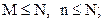n, N, M – натуральные числа.
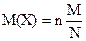, а ее дисперсия 
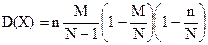(54)
функция вероятностей (53) гипергеометрического распределения стремится к соответствующей функции (47) биномиального закона.
