Закон распределения Пуассона.
Дискретная случайная величина Х имеет закон распределения Пуассона с параметром Ряд распределения закона Пуассона имеет вид:
Теорема. Математическое ожидание случайной величины Х, распределенной по закону Пуассона, совпадают и равны параметру При по закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматной линии, число отказов сложной системы в «нормальном режиме», число «требований на обслуживание», поступивших в единицу времени в системах массового обслуживания, и др.
|
, если она принимает значения 0, 1, 2, …, m, … (бесконечное, но счетное множество значений) с вероятностями 
(50)
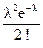
, т.е. M(X) = 
, 
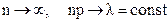закон распределения Пуассона является предельным случаем биномиального закона. Так как вероятность р мала, то закон распределения Пуассона называют еще законом редких явлений.
