Теорема Чебышева.
Теорема. Если Х 1, Х 2, …, Хn, … - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число Т.е. Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое количество независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым. Значит, среднее арифметическое достаточно большого количества независимых случайных величин утрачивает характер случайной величины. На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями. Или судят о качестве зерна по небольшой его пробе – число отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
|
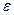, вероятность неравенства 
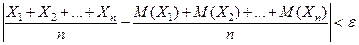будет как угодно близка к единице, если число случайных величин достаточно велико.
.
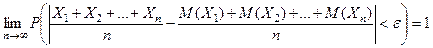