Пусть (X, Y) – непрерывная двумерная случайная величина.
Условной плотностью  распределения составляющих Х при данном значении Y = y называют отношение плотности совместного распределения f (x, y) системы (X, Y) к плотности распределения f 2(y) составляющей Y:
распределения составляющих Х при данном значении Y = y называют отношение плотности совместного распределения f (x, y) системы (X, Y) к плотности распределения f 2(y) составляющей Y:  . Аналогично определяется условная плотность составляющей Y при данном значении Х.
. Аналогично определяется условная плотность составляющей Y при данном значении Х.
Условным математическим ожиданием дискретной случайной величины Y при Х = х называют произведение возможных значений Y на их условные вероятности: 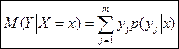 . Для непрерывных величин
. Для непрерывных величин  , где
, где  - условная плотность случайной величины Y при Х = х. Условное математическое ожидание
- условная плотность случайной величины Y при Х = х. Условное математическое ожидание 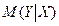 есть функция от х, которую называют функцией регрессии Y на Х. Аналогично определяются условное мат. ожидание Х и функция регрессии Х на Y.
есть функция от х, которую называют функцией регрессии Y на Х. Аналогично определяются условное мат. ожидание Х и функция регрессии Х на Y.

 распределения составляющих Х при данном значении Y = y называют отношение плотности совместного распределения f (x, y) системы (X, Y) к плотности распределения f 2(y) составляющей Y:
распределения составляющих Х при данном значении Y = y называют отношение плотности совместного распределения f (x, y) системы (X, Y) к плотности распределения f 2(y) составляющей Y:  . Аналогично определяется условная плотность составляющей Y при данном значении Х.
. Аналогично определяется условная плотность составляющей Y при данном значении Х.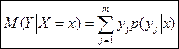 . Для непрерывных величин
. Для непрерывных величин  , где
, где  - условная плотность случайной величины Y при Х = х. Условное математическое ожидание
- условная плотность случайной величины Y при Х = х. Условное математическое ожидание 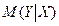 есть функция от х, которую называют функцией регрессии Y на Х. Аналогично определяются условное мат. ожидание Х и функция регрессии Х на Y.
есть функция от х, которую называют функцией регрессии Y на Х. Аналогично определяются условное мат. ожидание Х и функция регрессии Х на Y.


