Биномиальный закон распределения.Основные законы распределения. В данном параграфе рассмотрим основные законы распределения случайных величин, используемых для построения теоретико-вероятностных моделей реальных социально-экономических явлений. Биномиальный закон распределения. Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями где 0 < p < 1, q = 1 – p. Биномиальный закон представляет собой закон распределения числа Х = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р. Ряд распределения биномиального закона имеет вид:
Теорема. Математическое ожидание случайной величины Х, распределенной по биномиальному закону, M(X) = np, а ее дисперсия D(X) = npq (48) Следствие. Математическое ожидание частости Биномиальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, при моделировании цен активов, в теории стрельбы и в других областях.
|
(47)
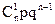
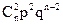
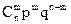
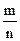события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью p, равно р, т.е. 
, а ее дисперсия 
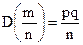(49)
