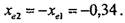ПРОЕКТИРОВОЧНЫЙ РАСЧЕТ ЗУБЧАТОЙ КОНИЧЕСКОЙ
ОРТОГОНАЛЬНОЙ ПЕРЕДАЧИ С КРУГОВЫМИ ЗУБЬЯМИ Рассчитать зубчатую коническую передачу с круговыми зубьями для одноступенчатого редуктора с моментом на выходе Частоты вращения входного и выходного валов передачи равны Конические колеса соответствуют осевой форме 1. Угол наклона зуба в среднем сечении Передача нереверсивная. Шестерня передачи относительно опор расположена консольно. Время безотказной работы Зубчатые колеса изготовлены из стали 40Х, закаленной по поверхности до твердости В качестве параметров исходного контура инструмента принять: коэффициент высоты головки зуба; коэффициент высоты ножки зуба; Расчет Определение допускаемых напряжений Расчет допускаемых напряжений по контакту и по изгибу не зависит от типа зубчатой передачи. Поскольку исходные данные для расчета рассматриваемой конической передачи с круговыми зубьями совпадают с аналогичными данными цилиндрической передачи (п. 3.1) и конической передачи с прямыми зубьями (п. 3.2), то в качестве допускаемых напряжений будем принимать значения, полученные в п.п. 3.1—3.2. Тогда 1. допускаемое напряжение усталостной прочности по контакту:
2. допускаемые напряжения усталостной прочности по напряжениям изгиба: для шестерни:=352,94 МПа; для колеса: Расчет геометрии передачи из условия прочности по контактным напряжениям. На этапе проектировочного расчета значение коэффициента динамичности нагрузки принимаем равным 3.3. Проектировочный расчет зубчатой конической передачи с круговыми зубьями 157 Для определения коэффициента концентрации нагрузки варительно вычислить величину конструктивного коэффициента лежат в диапазоне эффициент
Используя данные табл. 7.1.4, для заданного в условии консольного размещения шестерни относительно опор получаем
Аналогично можно определить значение коэффициента концентрации нагрузки при расчете на изгиб
Внешний диаметр колеса
Внешнее конусное расстояние конического зацепления и рабочая ширина колес: Для обеспечения выполнения геометрических и технологических условий изготовления конических передач количество зубьев шестерни следует вычислять по формуле [3, стр. 101]: 158 Глава 3. Передаточные механизмы
После подстановки исходных данных получаем
Поскольку количество зубьев может быть только целым числом, принимаем
Расчетное значение внешнего окружного модуля:
Полученное значение округляем до ближайшего из нормального ряда (табл. 7.1.2), т. е. полагаем
После этого уточним диаметры шестерни и колеса: Если округлить значение ширины колеса до ближайшего целого числа,
Уточняем значения коэффициента относительной ширины и коэффициента ширины зубчатого венца: 3.3. Проектировочный расчет зубчатой конической передачи с круговыми зубьями 159
Пересчитываем коэффициенты
Коэффициент смещения инструмента равносмещенной передачи (7.2.12):
|

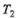 = 900 Н-м.
= 900 Н-м.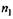 =210 об/мин и
=210 об/мин и 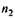 =70 об/мин соответственно (передаточное число и = 3).
=70 об/мин соответственно (передаточное число и = 3).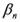 = 35°.
= 35°.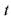 =10 000 часов в тяжелом режиме нагру- жения.
=10 000 часов в тяжелом режиме нагру- жения. , термообработка типа «улучшение» с последующей закалкой ТВЧ по контуру до заявленной твердости.
, термообработка типа «улучшение» с последующей закалкой ТВЧ по контуру до заявленной твердости.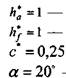 — коэффициент радиального зазора; — угол профиля рейки.
— коэффициент радиального зазора; — угол профиля рейки.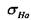 = 804 МПа;
= 804 МПа;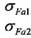 = 352,94 МПа.
= 352,94 МПа.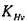 = 1,0.
= 1,0.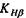 необходимо пред-
необходимо пред- , зависящую от коэффициента ширины зубчатого венца
, зависящую от коэффициента ширины зубчатого венца 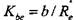 . Поскольку значения
. Поскольку значения 
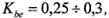 выбираем
выбираем 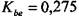 . Конструктивный ко-
. Конструктивный ко- с учетом (7.2.7) равен
с учетом (7.2.7) равен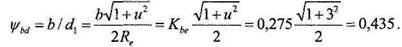

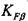 . Согласно табл. 7.1.5 запишем
. Согласно табл. 7.1.5 запишем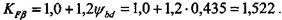
 рассчитывается по формуле 7.2.31, полученной из условия прочности по допускаемым контактным напряжениям, аналогичного (7.2.28), с той лишь разницей, что повышенная по отношению к прямозубым передачам прочность учитывается введением иного по величине поправочного коэффициента
рассчитывается по формуле 7.2.31, полученной из условия прочности по допускаемым контактным напряжениям, аналогичного (7.2.28), с той лишь разницей, что повышенная по отношению к прямозубым передачам прочность учитывается введением иного по величине поправочного коэффициента 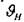 . При заданной в условии твердости зубьев в качестве расчетного принимаем следующее значение
. При заданной в условии твердости зубьев в качестве расчетного принимаем следующее значение 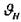 :
:

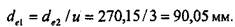
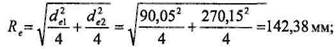
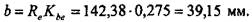
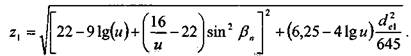

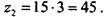
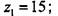

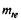 = 6.
= 6.
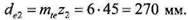
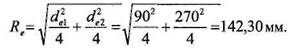

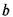 = 40 мм, то, как показывают дальнейшие расчеты, не выполняется условие прочности по контактным напряжениям. Поэтому ширину колеса следует сразу несколько увеличить:
= 40 мм, то, как показывают дальнейшие расчеты, не выполняется условие прочности по контактным напряжениям. Поэтому ширину колеса следует сразу несколько увеличить: 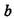 = 42 мм.
= 42 мм.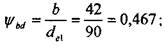

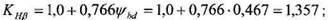
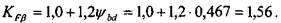


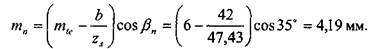

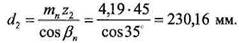
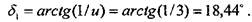
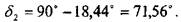
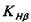 и
и  :
: