При рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклонений (гомоскедастичность):  .
.
Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
Требование постоянства дисперсии случайных отклонений может показаться странным. При каждом 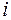 -м наблюдении имеется единственное значение
-м наблюдении имеется единственное значение  . Откуда же появляется дисперсия случайного члена? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной
. Откуда же появляется дисперсия случайного члена? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной  и соответственно с определенными случайными отклонениями
и соответственно с определенными случайными отклонениями 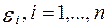 . Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую - при других.
. Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую - при других.
Однако на практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений  при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми - при других, но это означает, что априорная вероятность этого велика. На рис. 4,б показано как будет выглядеть характерная диаграмма рассеяния в случае гетероскедастичности остатков.
при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми - при других, но это означает, что априорная вероятность этого велика. На рис. 4,б показано как будет выглядеть характерная диаграмма рассеяния в случае гетероскедастичности остатков.
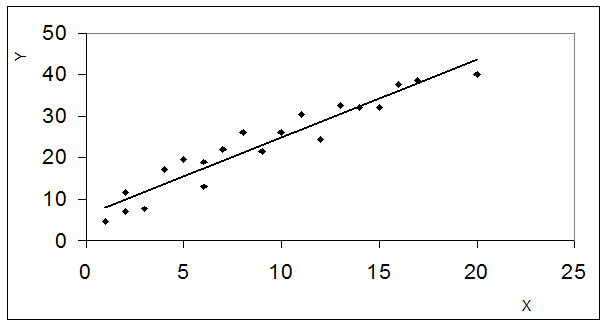
Рис. 4,а. Модель с гомоскедастичным случайным членом.
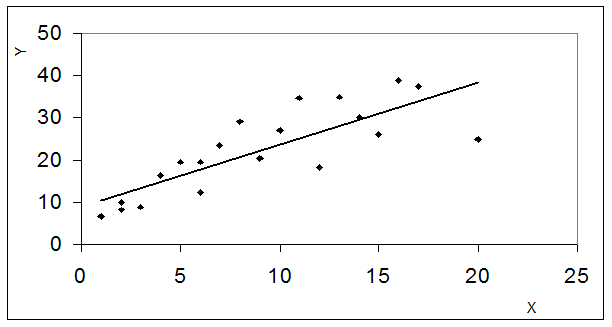 Рис. 4,б. Модель с гетероскедастичным случайным членом.
Рис. 4,б. Модель с гетероскедастичным случайным членом.

 .
.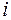 -м наблюдении имеется единственное значение
-м наблюдении имеется единственное значение  . Откуда же появляется дисперсия случайного члена? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной
. Откуда же появляется дисперсия случайного члена? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной  и соответственно с определенными случайными отклонениями
и соответственно с определенными случайными отклонениями 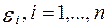 . Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую - при других.
. Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую - при других.
 Рис. 4,б. Модель с гетероскедастичным случайным членом.
Рис. 4,б. Модель с гетероскедастичным случайным членом.


