В данном случае также предполагается, что стандартное отклонение  пропорционально значению
пропорционально значению 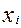 , т.е.
, т.е.  . Предполагается, что
. Предполагается, что  имеет нормальное распределение и отсутствует автокорреляция остатков. Тест Голдфелда—Квандта состоит в следующем:
имеет нормальное распределение и отсутствует автокорреляция остатков. Тест Голдфелда—Квандта состоит в следующем:
1. Все 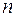 наблюдений упорядочиваются по величине
наблюдений упорядочиваются по величине 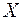 .
.
2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей  соответственно.
соответственно.
3. Оцениваются отдельные регрессии для первой подвыборки ( 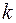 первых наблюдений) и для третьей подвыборки (
первых наблюдений) и для третьей подвыборки (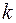 последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям
последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям 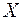 верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений
верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений  ) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений
) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений 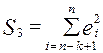 ).
).
4. Для сравнения соответствующих дисперсий строится следующая 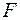 -статистика:
-статистика:
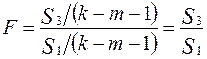
Здесь  число степеней свободы соответствующих выборочных дисперсий (
число степеней свободы соответствующих выборочных дисперсий (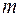 - количество объясняющих переменных в уравнении регрессии).
- количество объясняющих переменных в уравнении регрессии).
При сделанных предположениях относительно случайных отклонений построенная 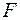 -статистика имеет распределение Фишера с числами степеней свободы
-статистика имеет распределение Фишера с числами степеней свободы  .
.
5. Если 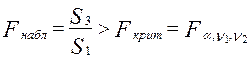 , то гипотеза об отсутствии гетероскедастичности отклоняется (здесь
, то гипотеза об отсутствии гетероскедастичности отклоняется (здесь  - выбранный уровень значимости).
- выбранный уровень значимости).
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений? Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: 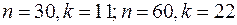 .
.
Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с  . При этом
. При этом 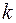 должно быть больше, чем
должно быть больше, чем 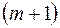 . Если нет уверенности относительно выбора переменной
. Если нет уверенности относительно выбора переменной 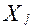 , то данный тест может осуществляться для каждой из объясняющих переменных.
, то данный тест может осуществляться для каждой из объясняющих переменных.
Этот же тест может быть использован при предположении об обратной пропорциональности между  , и значениями объясняющей переменной. При этом статистика Фишера примет вид:
, и значениями объясняющей переменной. При этом статистика Фишера примет вид:  .
.

 пропорционально значению
пропорционально значению 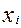 , т.е.
, т.е.  . Предполагается, что
. Предполагается, что  имеет нормальное распределение и отсутствует автокорреляция остатков. Тест Голдфелда—Квандта состоит в следующем:
имеет нормальное распределение и отсутствует автокорреляция остатков. Тест Голдфелда—Квандта состоит в следующем: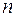 наблюдений упорядочиваются по величине
наблюдений упорядочиваются по величине 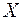 .
. соответственно.
соответственно.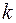 первых наблюдений) и для третьей подвыборки (
первых наблюдений) и для третьей подвыборки ( ) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений
) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений 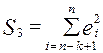 ).
).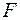 -статистика:
-статистика: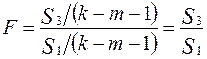
 число степеней свободы соответствующих выборочных дисперсий (
число степеней свободы соответствующих выборочных дисперсий (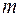 - количество объясняющих переменных в уравнении регрессии).
- количество объясняющих переменных в уравнении регрессии). .
.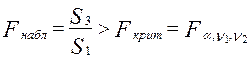 , то гипотеза об отсутствии гетероскедастичности отклоняется (здесь
, то гипотеза об отсутствии гетероскедастичности отклоняется (здесь  - выбранный уровень значимости).
- выбранный уровень значимости).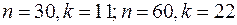 .
. . При этом
. При этом 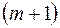 . Если нет уверенности относительно выбора переменной
. Если нет уверенности относительно выбора переменной 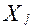 , то данный тест может осуществляться для каждой из объясняющих переменных.
, то данный тест может осуществляться для каждой из объясняющих переменных. .
.


