УСТОЙЧИВОСТЬ СИСТЕМЫ

Устойчивость системы – это свойство возвращаться к состоянию установившегося равновесия, после устранения возмущения, нарушившего равновесие.

Устойчивость является необходимым условием работоспособности системы.

Система неустойчива, если после снятия возмущения выходная величина неограниченно удаляется от первоначально установившегося режима.

Если график переходного процесса сходящийся, то система устойчива, а если расходящийся то система неустойчива.

Устойчивость системы характеризуется ее свободными движениями. Свободные движения системы описываются однородными дифференциальными уравнениями, т.е. уравнениями без правой части. Для определения устойчивости системы исследуется уравнение. Встречаются различные комбинации корней.

Если характеристическое уравнение имеет только вещественные и неравные корни, то с течением времени система будет удаляться от положения равновесия, т.е. будет неустойчивой.

Если характеристическое уравнение имеет пару комплексных сопряженных корней, то процесс будет затухать. При наличии пары чисто мнимых корней в системе возникают незатухающие гармонические колебания, система находится на границе устойчивости.

Если характеристическое уравнение имеет один нулевой корень, а все остальные корни вещественные и отрицательные, то система имеет множество состояний равновесия.

Для устойчивости необходимо, чтобы все вещественные корни характеристического уравнения были отрицательны, а комплексные корни имели отрицательную вещественную часть.

Исследуемая система является неустойчивой, так как корни характеристического уравнения не находятся в отрицательной плоскости относительно оси .
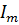