Уравнение прямой (в отрезках, проходящая через данную точку перпендикулярно данному вектору).Найдем уравнение прямой, проходящей через заданную точку Мо(хо;уо) перпендикулярно данному ненулевому вектору Возьмем на прямой произвольную точку М(х, у) и рассмотрим вектор
(11) Уравнение (11) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору. Вектор Уравнение (11) можно переписать в виде
где А и В — координаты нормального вектора, С = - Ахо - Byо — свободный член. Уравнение (12) есть общее уравнение прямой.
|
.
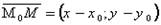
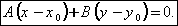.Поскольку векторы 
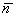и 
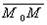перпендикулярны, то их скалярное произведение равно нулю: 
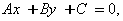(12)
