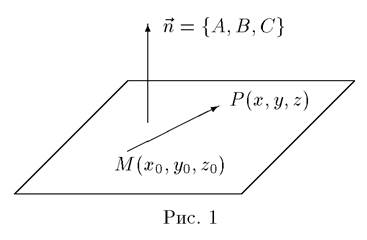
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу: Составить уравнение плоскости, проходящей через данную точку
= { A, B, C }. Решение. Пусть P (x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор
= { A, B, C } (рис.1).
Написав условие ортогональности этих векторов (
, MP) = 0 в координатной форме, получим:
Это и есть искомое уравнение. Вектор
= { A, B, C } называется нормальным вектором плоскости. Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости. Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:
где D = − Ax 0 − By 0 − Cz 0.
|