Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые L 1 и L 2 заданы уравнениями с угловыми коэффициентами Требуется найти угол φ, на который надо повернуть в положительное направлении прямую L 1 вокруг точки их пересечения до совпадения с прямой L 2.
Но
откуда легко получим величину искомого угла. Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая — второй, то правая часть формулы (10.12) берется по модулю, т. е. Если прямые L1 и L2 параллельны, то φ = 0 и Если прямые L1 и L2 перпендикулярны, то
|
и 
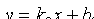(см. рис. 46).
Решение: Имеем 
(теорема о внешнем угле треугольника) или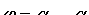 
. Если 
, то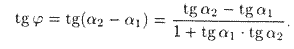
, 
, поэтому
(10.12)
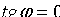. Из формулы (10.12) следует 
, т. е.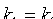 
. И обратно, если прямые L1 и L2 таковы, что 
.
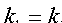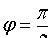. Следовательно,
. Отсюда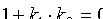 
, т. е. (или 
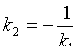). Справедливо и обратное утверждение. Таким образом, условием перпендикулярности прямых является равенство 
